slam学习笔记（1）

本文为高翔博士slam14讲学习笔记

旋转向量与旋转矩阵转化：

四元数表示的旋转：

三维旋转可以由单位四元数来描述，四元数也具有实部和虚部，类似于二维平面中的复数

用eigen包可以进行所有不同类型数之间的转化

群：集合加代数运算结构，G=（A，.）

李群：一种光滑连续的群

李代数：由一个集合，一个数域，一个二元运算（也称为李括号）组成 g=(R^3,R,x)，构成一个李代数

李代数表示在李群某一位置的导数特征

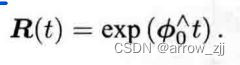
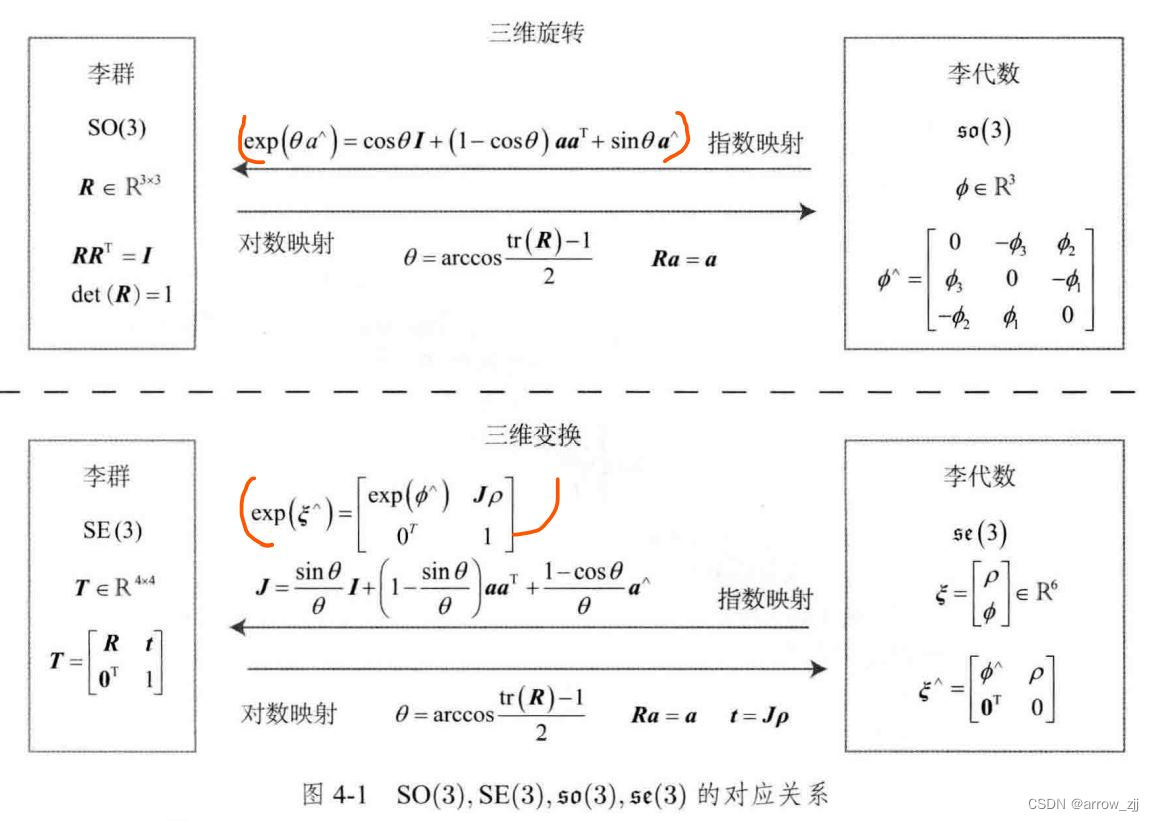
李群李代数转换，指数映射与对数映射

对于so，指数映射值罗德里格斯公式

BCH近似：

 左乘微小旋转，李群上的相乘等于李代数上的变换相加

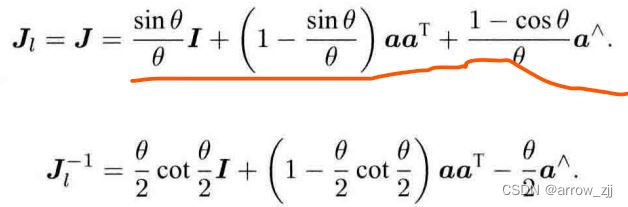
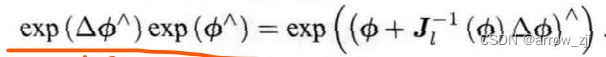
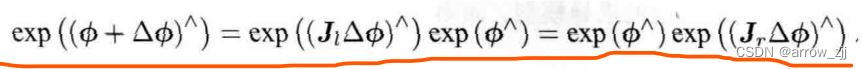
实际中常见的例子

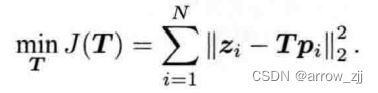
构建有关位姿的导数：

1.李代数表示位姿，通过李代数加法求导（因为求导是要依赖于减法运算）

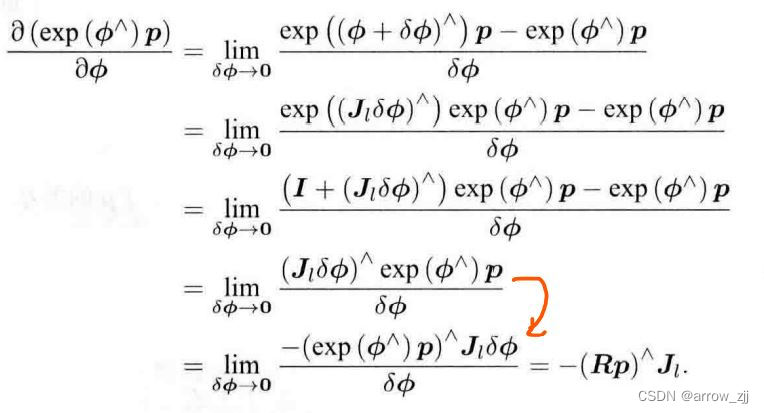
2.扰动模型

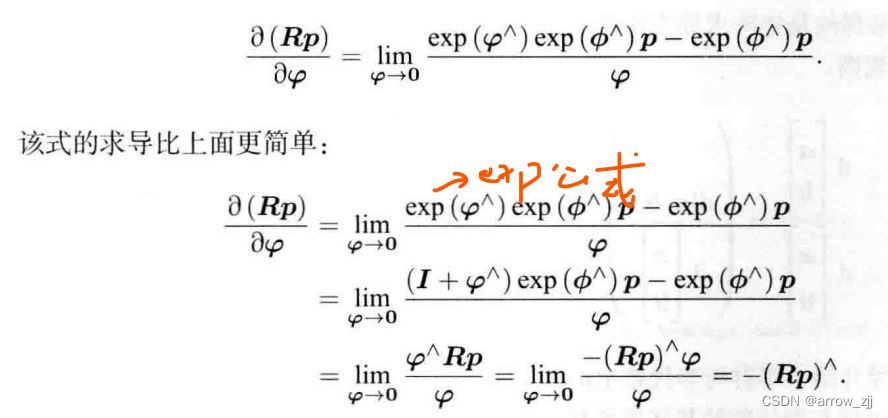
SE(3)上的李代数求导：

 

 利用sophus，可以求解李代数相关的问题，利用Sophus::SO3d，从旋转矩阵或四元数构造李群

.matrix获取矩阵值，.log获取李代数

hat -> ^ ,vee -> ,exp直接转化为旋转矩阵，log直接旋转矩阵转化为向量

图像与相机

像素坐标与世界坐标的转化：

 相机的归一化平面是Z=1情况下的平面

双目相机成像模型：

 

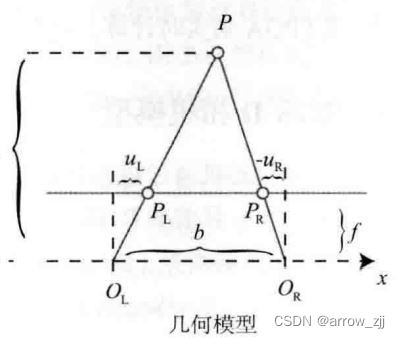
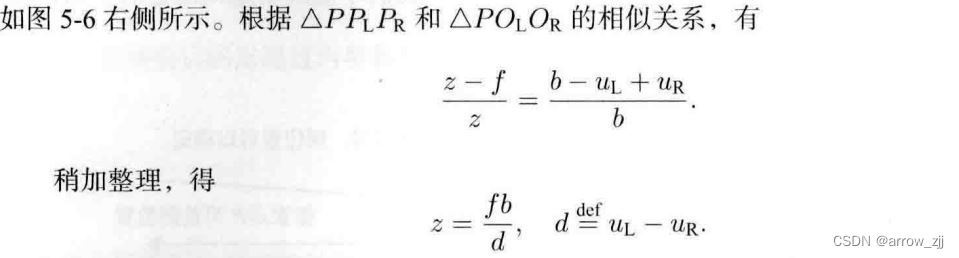
 RGB-D相机的使用局限：
红外光深度测量相机，易受日光和其他红外光的干扰，没有调制的情况下，无法使用多个RGB-D相机，对于透材和不易反射的物质，接受 不到反射光线

opencv图像操作：

图像数据在内存中的存储：

unsigned char image[480][640]，注意与像素坐标中的x,y刚好是相反的
#include<opencv2/core/core.hpp>

#include<opencv2/highgui/highgui.hpp>

cv::imread  image::cols  image::rows  image::channels

cv::waitKey(0) 程序暂停，等待输入

 opencv图像数据访问：
row_ptr = image.ptr<unsigned char>(y)  row_ptr[0]  or

image.ptr<unsigned char>(y) [x]

image.clone()，深拷贝数据，完全独立的拷贝

对规律命名图片的批量拷贝：定义格式函数

boost::format fmt("./%s/%d.%s")

读取时对int变量更新，覆盖%d函数的位置

非线性优化：
核心方程 

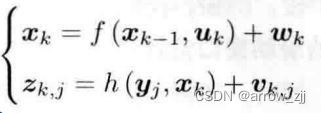
 第一个为运动方程，第二个为观测方程，u表示所有时刻的输入，z表示所有时刻的观测

对机器人状态的估计，从概率学角度来看

x为机器人位姿，y为机器人路标点（landmark）

对于sfm问题，只有观测z，没有输入u

 

 直接求后验分布很困难，后验变似然加先验

 求最大后验概率等价于求最大化似然和先验的乘积，在没有先验的情况下，可以求最大似然估计

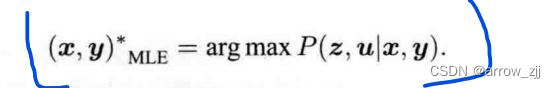
上述公式中：已知道观测数据z和输入数据u（通常由IMU输入），可理解为在什么样的状态下，最可能产生现在观测到的数据 

在高斯分布下，最大似然能够有较简单的形式：求解最大似然估计标准操作，求解概率密度函数的负对数

概念补充：

 

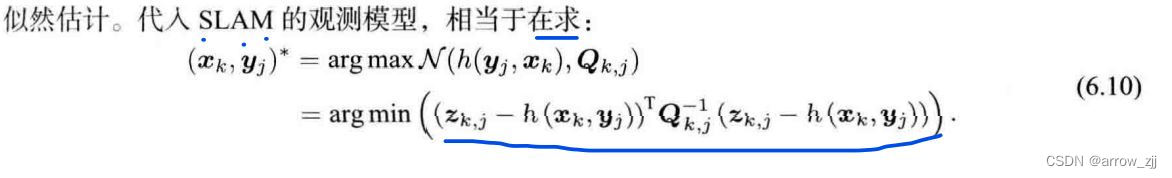
 中间矩阵为高斯分布协方差矩阵的逆

进一步总结：

因为要同时优化多个项，每个项都仅由少数几个变量来控制，同时z和u是相互独立的，由此可得如下的式子：

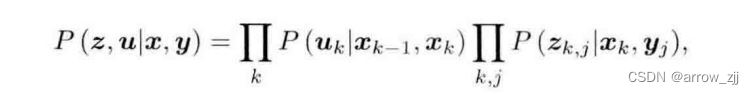
 表述每一项的意义：
已知u，x(k-1)和x(k)概率上最有可能的差距，已知z，最有可能当下的位姿和路标点，

故由此可以定义误差：

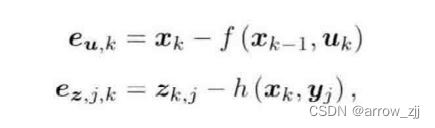
 上上个公式，是服从于高斯分布的，连乘取对数，可以变为相加的形式，每一项都是相对简单的变量，使上述公式最大化，由高斯分布的性质可得，相当于求：

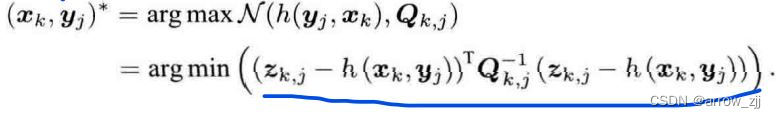
 Q为信息矩阵，高斯分布协方差矩阵之逆

 非线性最小二乘问题的数值求解：

典型代表，牛顿法和最速下降法，分别为泰勒二阶近似和泰勒一阶近似

两种方法各有优缺点，最速下降法过于贪心，容易走锯齿形状路线，而牛顿法又H矩阵计算较为麻烦，在slam问题中，我们探究最小二乘问题的优化，主要使用高斯牛顿和列文伯格-马夸尔特

牛顿法和高斯牛顿法，LM原理及对比牛顿法和高斯牛顿法对比_猪猪侠的猪猪女孩的博客-程序员宝宝_牛顿法 高斯牛顿法 - 程序员宝宝 (cxybb.com)

LM更加鲁棒，当slam接近于病态问题时，采用LM算法效果较好，但是速度会有所折扣

Ceres曲线拟合：

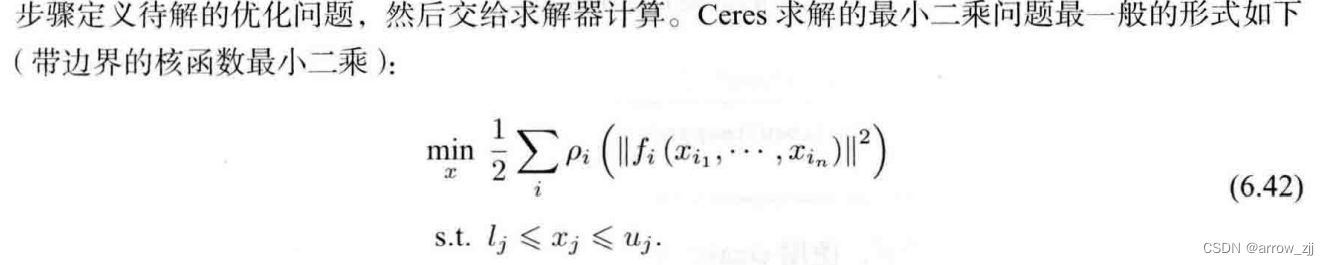
使用条件：1.定义每一个参数块 2.定义残差块的计算方式 3.定义残差块雅可比计算方式（可选择）4.参数块和残差块加入Ceres定义的 Problem对象中，调用solve函数求解

g2o曲线拟合：节点为优化变量，边为误差项

g2o::BaseUnaryEdge:(5条消息) g2o源码分析之BaseBinaryEdge_肥鼠路易的博客-CSDN博客https://blog.csdn.net/weixin_44991673/article/details/117250252

BaseUnaryEdge<D,E>，D为测量值，E为测量值的数据类型

g2o::BaseVertex：(5条消息) g2o源码分析之BaseVertex_肥鼠路易的博客-CSDN博客

<D,E> D代表节点的维度，E代表存储该节点的数据类型

g2o 小结 - 知乎 (zhihu.com)

typedef g2o::BlockSolver<g2o::BlockSolverTraits<3, 1>> BlockSolverType; // 每个误差项优化变量维度为3，误差值维度为1

对于slam问题，带有许多个相机位姿和观测点，g2o提供大量的边和节点，较为方便。而同样使用Ceres，还需要定义一个损失函数，比较麻烦。

实践章节：

视觉里程计

前端（即视觉里程计），粗略估计相机的运动，给后端优化提供较好的初始值。

特征点法和直接法两种

路标：图像特征，一个图像的特征由关键点和描述子组成

关键点匹配，采用快速近似最近邻

实际操作：

 单目相机：
2D-2D，对极几何，针对对极几何的情况

 

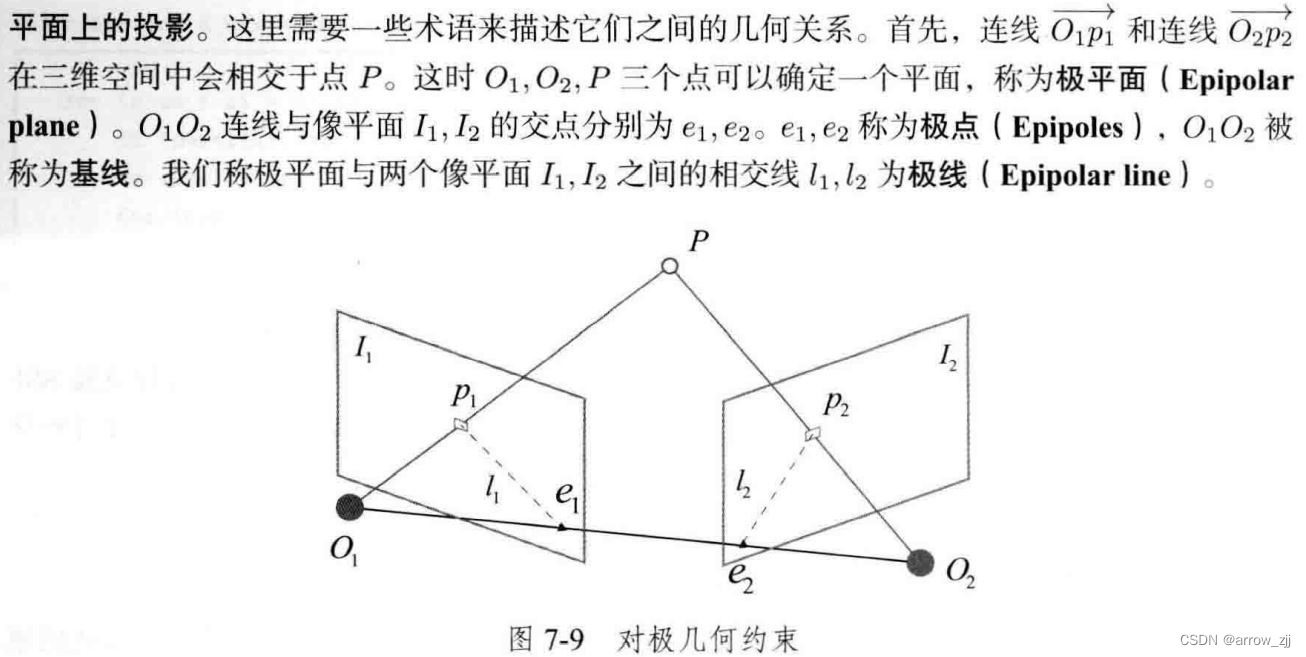
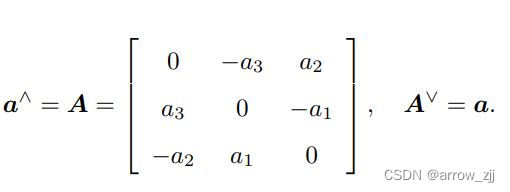
 与a^相乘相当于做差集

 x1，x2是归一化平面上的点（相机坐标系），计算方面通常用更加简洁的本质矩阵E来定义，p1和p2是图像坐标系上的点

1.E是由对极约束来定义的，乘以任意非零系数后，对极约束仍然满足，不同尺度下是等价的

2.由t和R得到，自由度为6

综合以上两点，得到E的自由度为5 (5条消息) 3月12日 对极几何，本征矩阵，基础矩阵，F/E矩阵计算，恢复旋转与平移，三角化视图重建_Hali_Botebie的博客-CSDN博客

通过八点法计算其值，然后进行奇异值分解，得到相应的R和T

单应矩阵：用于刻画共面的情形

 

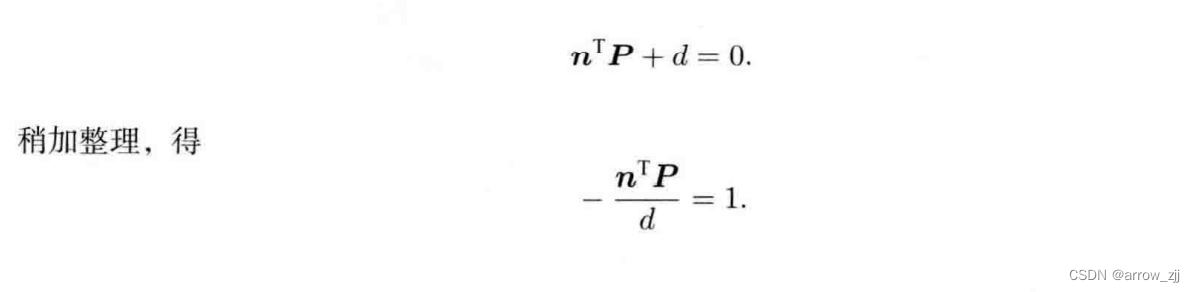
 单应矩阵自由度为8，相比较于本质矩阵，自由度增加，在相机纯旋转时，本质矩阵自由度退化，多余自由度由数据噪声来决定，所以通常同时计算单应矩阵和本质矩阵，选择重投影误差较小的值来计算。

单目运算缺点：本质矩阵分解得到的t是具有尺度的，常数恒成立性

由于E本身具有尺度等价性，运动构建也具有尺度不变性，用首两张图片的平移来得到t，并以其为单位一来进行后续计算（初始化方法1）

特征点深度均值为1（初始化方法2），控制整个地图的规模

仅有纯旋转的情况下，导致t为零，那么E也为零，无法计算R，但可以通过H矩阵来求旋转，但是特征点的空间位置我们无法得到

左右平移进行较好的初始化，运动不能太小，否则结果会很不稳定

 RANSAC YYDS

三角测量：

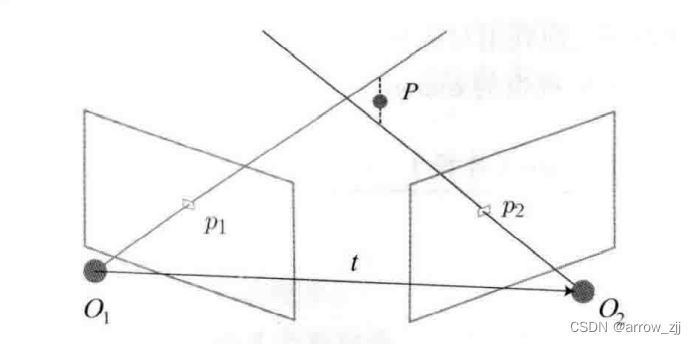
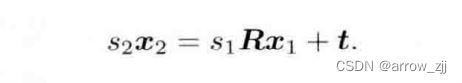
三角测量，平移得到的，纯旋转是无法得到三角测量形状，进而测量深度的，机器人纯旋转效果很不好

提高精度的话：（1）提高相机分辨率，降低单个像素的尺寸 （2）t增大，图像变换较大，导致交集很少，容易丢失信息

代码实现： （1）函数参数传递多以引用为主，减少内存分配，加快速度

                   （2）m:matchs，m.queryIdx，m.trainIdx，分别指向两对成功匹配点的索引，用于从关键点vector中提取成功匹配的坐标

                  （3）keypoint(vector).pt，可以得到该关键点的坐标

3D-2D: PNP

可以用于表示世界坐标系三维点和相机坐标系中的位姿关系，也可以表示两个坐标系之间的关系

已知点的像素坐标及其深度：求解相机旋转和平移，变换矩阵

直接线性变换（DLT):

 

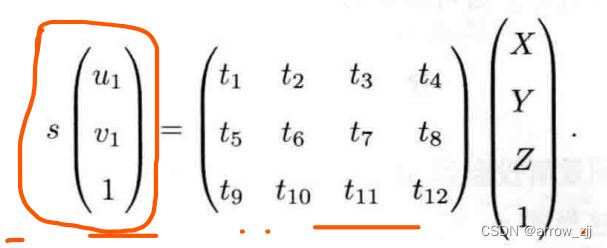
 需要至少六对点才能得到数值解

p3p也是一种求解pnp问题的方法，仅需要三对点就可以得到函数的解，鲁棒性不强

BA（对初步得到的相机位姿和空间点进行优化） 核心，重投影误差

先估计初步值，在通过BA进行优化，得到较为精确位姿估计值

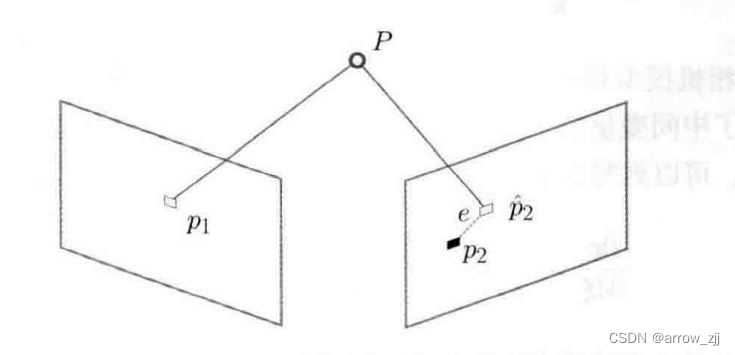
重投影误差示意图

 

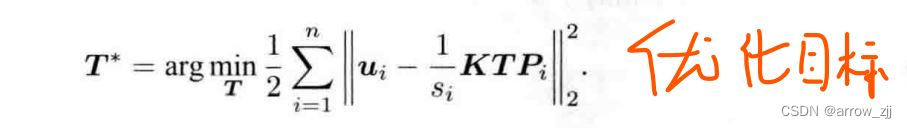
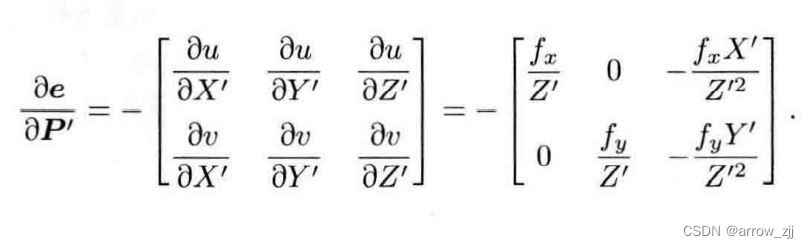
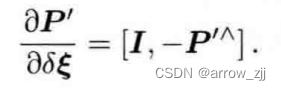
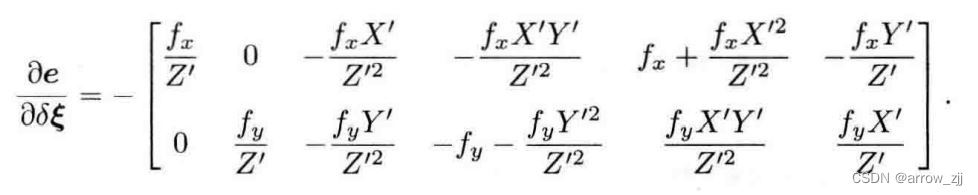
 至此，雅可比矩阵解析形式即可得到

编程求解:深度图如何转化为三维坐标：

需要知道3d坐标点和相对应的变换后的2D坐标点

    Point2d p1 = pixel2cam(keypoints_1[m.queryIdx].pt, K);
    pts_3d.push_back(Point3f(p1.x * dd, p1.y * dd, dd));

solvePnP(pts_3d, pts_2d, K, Mat(), r, t, false);

cv::Rodrigues(r, R); // r为旋转向量形式，用Rodrigues公式转换为矩阵

 手写高斯牛顿法实现非线性优化：核心步骤

H = J *J.T  b = J * e

Eigen::Vector3d pc = pose * points_3d[i]; //转化为相机坐标系

Eigen::Vector2d proj(fx * pc[0] / pc[2] + cx, fy * pc[1] / pc[2] + cy);//转化为像素坐标系

Eigen::Vector2d e = points_2d[i] - proj;//计算误差，误差为二维

cost += e.squaredNorm();//计算损失

Eigen::Matrix<double, 2, 6> J;//雅可比矩阵的解析计算

H += J.transpose() * J;
b += -J.transpose() * e;

dx = H.ldlt().solve(b);

pose = Sophus::SE3d::exp(dx) * pose;//参数更新，指数化dx

使用g2o优化：

BaseVertex<优化量的个数，优化量的类型>

BaseUnaryEdge<计算结果和对比值得维度，上面定义得vertext类型>

/// vertex and edges used in g2o ba
/// 定义顶点和边
class VertexPose : public g2o::BaseVertex<6, Sophus::SE3d> {
public:
  EIGEN_MAKE_ALIGNED_OPERATOR_NEW;

  virtual void setToOriginImpl() override {
    _estimate = Sophus::SE3d();//估计值的初始化
  }

  /// left multiplication on SE3
  virtual void oplusImpl(const double *update) override {
    Eigen::Matrix<double, 6, 1> update_eigen;
    update_eigen << update[0], update[1], update[2], update[3], update[4], update[5];
    _estimate = Sophus::SE3d::exp(update_eigen) * _estimate;//估计值的更新
  }

  virtual bool read(istream &in) override {}

  virtual bool write(ostream &out) const override {}
};

class EdgeProjection : public g2o::BaseUnaryEdge<2, Eigen::Vector2d, VertexPose> {
public:
  EIGEN_MAKE_ALIGNED_OPERATOR_NEW;

  EdgeProjection(const Eigen::Vector3d &pos, const Eigen::Matrix3d &K) : _pos3d(pos), _K(K) {}//不需要定义，可直接使用

  virtual void computeError() override {
    const VertexPose *v = static_cast<VertexPose *> (_vertices[0]);//创建顶点对象
    Sophus::SE3d T = v->estimate();//返回当前估计值
    Eigen::Vector3d pos_pixel = _K * (T * _pos3d);
    pos_pixel /= pos_pixel[2];
    _error = _measurement - pos_pixel.head<2>();//计算误差
  }

  //计算雅可比矩阵，数值法或者解析法
  virtual void linearizeOplus() override {
    const VertexPose *v = static_cast<VertexPose *> (_vertices[0]);
    Sophus::SE3d T = v->estimate();
    Eigen::Vector3d pos_cam = T * _pos3d;
    double fx = _K(0, 0);
    double fy = _K(1, 1);
    double cx = _K(0, 2);
    double cy = _K(1, 2);
    double X = pos_cam[0];
    double Y = pos_cam[1];
    double Z = pos_cam[2];
    double Z2 = Z * Z;
    _jacobianOplusXi
      << -fx / Z, 0, fx * X / Z2, fx * X * Y / Z2, -fx - fx * X * X / Z2, fx * Y / Z,
      0, -fy / Z, fy * Y / (Z * Z), fy + fy * Y * Y / Z2, -fy * X * Y / Z2, -fy * X / Z;
  }

  virtual bool read(istream &in) override {}

  virtual bool write(ostream &out) const override {}

private:
  Eigen::Vector3d _pos3d;
  Eigen::Matrix3d _K;
};

//g2o图优化问题求解

void bundleAdjustmentG2O(
  const VecVector3d &points_3d,
  const VecVector2d &points_2d,
  const Mat &K,
  Sophus::SE3d &pose) {

  // 构建图优化，先设定g2o
  typedef g2o::BlockSolver<g2o::BlockSolverTraits<6, 3>> BlockSolverType;  // pose is 6, landmark is 3
  typedef g2o::LinearSolverDense<BlockSolverType::PoseMatrixType> LinearSolverType; // 线性求解器类型
  // 梯度下降方法，可以从GN, LM, DogLeg 中选
  auto solver = new g2o::OptimizationAlgorithmGaussNewton(
    g2o::make_unique<BlockSolverType>(g2o::make_unique<LinearSolverType>()));
  g2o::SparseOptimizer optimizer;     // 图模型
  optimizer.setAlgorithm(solver);   // 设置求解器
  optimizer.setVerbose(true);       // 打开调试输出

  // vertex
  VertexPose *vertex_pose = new VertexPose(); // camera vertex_pose
  vertex_pose->setId(0);
  vertex_pose->setEstimate(Sophus::SE3d());
  optimizer.addVertex(vertex_pose);

  // K
  Eigen::Matrix3d K_eigen;
  K_eigen <<
          K.at<double>(0, 0), K.at<double>(0, 1), K.at<double>(0, 2),
    K.at<double>(1, 0), K.at<double>(1, 1), K.at<double>(1, 2),
    K.at<double>(2, 0), K.at<double>(2, 1), K.at<double>(2, 2);

  // edges
  int index = 1;
  for (size_t i = 0; i < points_2d.size(); ++i) {
    auto p2d = points_2d[i];
    auto p3d = points_3d[i];
    EdgeProjection *edge = new EdgeProjection(p3d, K_eigen);
    edge->setId(index);
    edge->setVertex(0, vertex_pose);
    edge->setMeasurement(p2d);
    edge->setInformation(Eigen::Matrix2d::Identity());
    optimizer.addEdge(edge);
    index++;
  }

  chrono::steady_clock::time_point t1 = chrono::steady_clock::now();
  optimizer.setVerbose(true);
  optimizer.initializeOptimization();
  optimizer.optimize(10);
  chrono::steady_clock::time_point t2 = chrono::steady_clock::now();
  chrono::duration<double> time_used = chrono::duration_cast<chrono::duration<double>>(t2 - t1);
  cout << "optimization costs time: " << time_used.count() << " seconds." << endl;
  cout << "pose estimated by g2o =\n" << vertex_pose->estimate().matrix() << endl;
  pose = vertex_pose->estimate();
}

g2o代码阅读 高翔Slambook第七讲：3d2d非线性优化 - 云+社区 - 腾讯云 (tencent.com)

g2o中定义g2o::BlockSolverTraits<p,l>的时候，p和l要如何设置？ - 知乎 (zhihu.com)

从零开始一起学习SLAM | 掌握g2o边的代码套路 - 知乎 (zhihu.com)

总结：一元边，<优化变量维度，值得维度>

二元边，<优化变量维度，另一端优化变量维度>

BA优化可以对整个slam系统进行优化，大规模计算主要用于后端，对于前端，主要考虑局部范围内得小型BA优化，实时求解（提供初值）并进行优化

Eigen的vector取头尾或切片

获取向量的前n个元素：vector.head(n);
获取向量尾部的n个元素：vector.tail(n);
获取从向量的第i个元素开始的n个元素：vector.segment(i,n);

3D-3D ：ICP

同样具有两种方法：利用线性代数求解（SVD），和利用非线性优化得解

误差：

 矩阵的秩：

矩阵的秩是线性代数中的一个概念。在线性代数中，一个矩阵A的列秩是A的线性独立的纵列的极大数，通常表示为r(A)，rk(A)或rank A。 [1] 

在线性代数中，一个矩阵A的列秩是A的线性独立的纵列的极大数目。类似地，行秩是A的线性无关的横行的极大数目。即如果把矩阵看成一个个行向量或者列向量，秩就是这些行向量或者列向量的秩，也就是极大无关组中所含向量的个数。

满秩矩阵是指最大秩，是矩阵是否可逆的重要标志

SVD分解相关知识：SVD-矩阵奇异值分解 —— 原理与几何意义 - 知乎 (zhihu.com)

非线性优化：

目标函数：

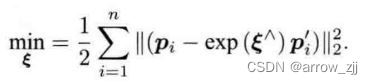
 李代数扰动求导：

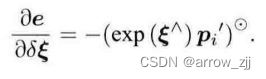
ICP 问题存在无穷多和唯一解，唯一解的情况下，不用寻找初始值，随便取值即可 

匹配已知的情况下，有解析解，迭代解是为了和pnp问题配对，用同一个模式进行深度点未知和深度点已知的求解。

 矩阵行列式不为零，证明矩阵满秩，矩阵方程必有唯一解，当其行列式为零，矩阵不满秩，无解或有无穷多解

BlockSolver需要自定义数据维度的大小，BlockSolverX采用动态分配的方式

边：计算误差和雅可比矩阵，供给内部的增量方程进行运算

顶点：初始化待优化值（手动设置），利用增量方程计算出来的值和结构进行参数更新