本文详细介绍了如何使用Markdown和LaTeX来设置文字颜色、高亮文本，并重点讲解了数学表达式的各种表示，包括向量、矩阵、行列式、阵列、省略号、范数与内积、分段函数与方程组、二项组合等。此外，还涵盖了字母字体、空格、逻辑符号、集合运算和特殊符号的使用方法，以及箭头的输入大全。
文章目录
文字设置
颜色设计
有关链接： TreasureAIMarkdown文字颜色高亮字体字号设置
张三 可表示为 <font color='red'>张三</font>
高亮文本
- highlight 1 可表示为
==highlight 1== - highlight 2 可表示为
<mark>highlight 2</mark> - 使用````符号
数学表达式相关
有关链接: YuYunTan----KATEX公式编辑器符号大全-CSDN的Mardown公式支持
向量, 矩阵, 行列式
使用 MathJax 渲染 LaTex 数学公式，详见 math.stackexchange.com，在 Markdown 中输入数学公式需要 LaTeX 语法的支持。参考链接
向量
- 向量形式给字母加粗
\pmb{x}. 如向量 x x x写为$\pmb{x}$, 显示为 x \pmb{x} x ; 加粗倾斜写为$\boldsymbol{x}$，显示为 x \boldsymbol{x} x - 向量形式给字母加上标箭头
\vec{x}, 显示为 x ⃗ \vec{x} x；或者写为\overrightarrow{x}, 显示为 x → \overrightarrow{x} x(不推荐)
矩阵
使用\begin{matrix} --- \end{matrix|, 虚线部分写具体的矩阵元素，同行各元素间用&分开，每行结尾用反斜杠\\隔开,最后一行无须使用反斜杠\\
常用语法
- 若元素需要用
圆括号包裹, 则将matrix换为pmatrix。如```
$$\begin{pmatrix}
1&1&1\\
1&1&1\\
1&1&1
\end{pmatrix}$$
显示为
(
1
1
1
1
1
1
1
1
1
)
\begin{pmatrix}1&1&1\\1&1&1\\1&1&1\end{pmatrix}
111111111
- 若元素需要用
中括号包裹, 则将matrix换为bmatrix。
$$\begin{bmatrix}
1&1&1\\
1&1&1\\
1&1&1
\end{bmatrix}$$
[ 1 1 1 1 1 1 1 1 1 ] \begin{bmatrix}1&1&1\\1&1&1\\1&1&1\end{bmatrix} 111111111
不常用语法
- 若元素需要用
花括号包裹, 则将matrix换为Bmatrix。 - 若元素需要用
单竖线包裹, 则将matrix换为vmatrix。 - 若元素需要用
双竖线包裹, 则将matrix换为Vmatrix。
-------花括号----------
$$\begin{Bmatrix}
1&1\\
1&1
\end{Bmatrix}$$
-------单竖线----------貌似不适用多行
$$\begin{vmatrix}
1&1
\end{vmatrix}$$
-------双竖线----------貌似不适用多行
$$\begin{Vmatrix}
1&1
\end{Vmatrix}$$
分别显示为
{
1
1
1
1
}
\begin{Bmatrix} 1&1\\ 1&1 \end{Bmatrix}
{1111}
∣
1
1
∣
\begin{vmatrix} 1&1 \end{vmatrix}
11
∥
1
1
∥
\begin{Vmatrix} 1&1 \end{Vmatrix}
11
行列式
以\begin{array}{对齐方式}---\end{array}构建，其中虚线部分为具体的行列式构成元素，各元素之间用&隔开，每行用\\隔开.包裹符号：左边符号则在\begin{array}前写\left所需符号; 右边符号则在\end{array}后写\right所需符号。对齐方式为居中对齐用字母c，左对齐用字母l，右对齐用字母r。默认（标注对齐方式的部分为空，包裹对齐方式的大括号不可省略）为居中对齐
如
$$
\left|
\begin{array}{ccc}
1 & 0 & 0 \\
-5 & 2 & 3\\
3 & 3 & 5
\end{array}
\right|
$$
显示为
∣
1
0
0
−
5
2
3
3
3
5
∣
\left| \begin{array}{ccc} 1 & 0 & 0 \\ -5 & 2 & 3\\ 3 & 3 & 5 \end{array} \right|
1−53023035
使用单竖线矩阵的效果如下
∣
1
0
0
−
5
2
3
3
3
5
∣
\begin{vmatrix} 1 & 0 & 0 \\ -5 & 2 & 3\\ 3 & 3 & 5 \end{vmatrix}
1−53023035
阵列
基本语法同行列式。无包裹符号（即不需要\left,\right符号）不同的是阵列有时会添加一些横线（\hline）竖线（写于对齐方式处, 直接用竖线即可|）如
$$
\begin{array}{c|cc}
1 & 0 & 0 \\
\hline
-5 & 2 & 3\\
3 & 3 & 5
\end{array}
$$
显示为：
1
0
0
−
5
2
3
3
3
5
\begin{array}{c|cc} 1 & 0 & 0 \\ \hline -5 & 2 & 3\\ 3 & 3 & 5 \end{array}
1−53023035
省略号
中间横省略号：\cdots $\cdots$显示为
1
,
2
,
3
,
⋯
,
n
1,2,3,\cdots,n
1,2,3,⋯,n
底层横省略号：\cdots $\ldots$显示为
1
,
2
,
3
,
…
,
n
1,2,3, \ldots,n
1,2,3,…,n
竖省略号：\vdots$\vdots$显示为
⋮
\vdots
⋮
斜省略号：\ddots$\cdots$显示为
⋱
\ddots
⋱
范数与内积
使用$\parallel x\parallel$ 显示为
∥
x
∥
\parallel x\parallel
∥x∥
使用$\langle x,y \rangle$ 显示为
⟨
x
,
y
⟩
\langle x,y\rangle
⟨x,y⟩
分段函数与方程组
使用\begin{cases}----\end{cases}语句结构，每个表达式结束用\\
如
$$f(x)=\begin{cases}
1, x>0\\
0, x\leq0
\end{cases}$$
显示为：
f
(
x
)
=
{
1
,
x
>
0
0
,
x
≤
0
f(x)=\begin{cases} 1, x>0\\ 0, x\leq0 \end{cases}
f(x)={1,x>00,x≤0
$$\begin{cases}
a_{11}x_1+a_{12}x_2=3\\
a_{21}x_1+a_{22}x_2=4
\end{cases}$$
显示为：
{
a
11
x
1
+
a
12
x
2
=
3
a
21
x
1
+
a
22
x
2
=
4
\begin{cases} a_{11}x_1+a_{12}x_2=3\\ a_{21}x_1+a_{22}x_2=4\\ \end{cases}
{a11x1+a12x2=3a21x1+a22x2=4
$$\begin{aligned}
a_{11}x_1+a_{12}x_2=3\\
a_{21}x_1+a_{22}x_2=4
\end{aligned}$$
显示为
a
11
x
1
+
a
12
x
2
=
3
a
21
x
1
+
a
22
x
2
=
4
\begin{aligned} a_{11}x_1+a_{12}x_2=3\\ a_{21}x_1+a_{22}x_2=4 \end{aligned}
a11x1+a12x2=3a21x1+a22x2=4
如需编号需要使用\tag{}语句，示例如下：
$$\begin{aligned}
a_{11}x_1+a_{12}x_2=3\\
a_{21}x_1+a_{22}x_2=4 \tag{1}
\end{aligned}$$
显示为
a
11
x
1
+
a
12
x
2
=
3
a
21
x
1
+
a
22
x
2
=
4
(1)
\begin{aligned} a_{11}x_1+a_{12}x_2=3\\ a_{21}x_1+a_{22}x_2=4 \tag{1} \end{aligned}
a11x1+a12x2=3a21x1+a22x2=4(1)
二项组合
${上位公式 \choose 下位公式}$。例子：从
n
n
n 个元素中选取
m
m
m 个元素:
(
n
m
)
{n\choose m}
(mn)
字母字体
- 镂空的黑体（Blackboard Bold）：
$\mathbb{字母}$，如$\mathbb{E}, 显示为 E \mathbb{E} E - 打印机字体（Typewriter）：
$\mathtt{E}$，显示 E \mathtt{E} E - 无衬线体（Sans Serif）:
$\mathsf{E}$，显示 E \mathsf{E} E - 黑体（boldface）:
$\mathbf{E}$，显示为 E \mathbf{E} E - 罗马体（roman）：
$\mathrm{E}$，显示为 E \mathrm{E} E - 书法体（calligraphic ）:
$\mathcal{E}$，显示为 E \mathcal{E} E - 手写体(script) ：
$\mathscr{E}$，显示为 E \mathscr{E} E - 德国哥特体(Fraktur)：
$\mathfrak{E}$，显示为 E \mathfrak{E} E - 斜体(italic):
$\mathit{E}$，显示为 E \mathit{E} E
空格
| 空格特征 | 代码语句 | 视觉显示 |
|---|---|---|
| 无空格正常 | $ab$ | 显示为 a b ab ab |
| 紧贴 | $a\!b$ | 显示为 a b a\! b ab |
| 小空格 | $a~b$ | 显示为 a b a~b a b |
| 小空格 | $a\,b$ | 显示为 a b a\,b ab |
| 中等空格 | $a\;b$ | 显示为 a b a\;b ab |
| 四字格 | $a\quad b$ | 显示为 a b a\quad b ab |
| 八字格 | $a\qquad b$ | 显示为 a b a\qquad b ab |
数学运算
四则运算
- 加减运算：
$x\pm y$显示为： x ± y x\pm y x±y - 减加运算：
$x\mp y$显示为： x ∓ y x\mp y x∓y - 叉乘运算：
$x\times y$显示为： x × y x\times y x×y - 点乘运算：
$x\cdot y$显示为： x ⋅ y x\cdot y x⋅y - 星乘运算：
$x\ast y$显示为： x ∗ y x\ast y x∗y - 除法运算：
$x\div y$显示为： x ÷ y x\div y x÷y - 斜杠除法运算：
$x/ y$显示为： x / y x/y x/y - 分式运算：
$x\over y$或$\frac{x}{y}$显示为： x y x\over y yx， x y \frac{x}{y} yx
高级运算
- 平均数运算：
$\overline{算式表达式}$显示为： 算式表达式 ‾ \overline{算式表达式} 算式表达式 - 开二次方运算：
$\sqrt{算式表达式}$显示为： 算式表达式 \sqrt{算式表达式} 算式表达式 - 开
n
n
n 次方运算：
$\sqrt[n]{算式表达式}$显示为： 算式表达式 n \sqrt[n]{算式表达式} n算式表达式 - 对数运算：
$\log(算式表达式)$， 显示为： log ( 算式表达式 ) \log(算式表达式) log(算式表达式) - 极限运算：
$lim_{写于下部的变量极限}^{写于上部的变量极限}$，显示为： l i m 写于下部的变量极限 写于上部的变量极限 lim_{写于下部的变量极限}^{写于上部的变量极限} lim写于下部的变量极限写于上部的变量极限 - 将变量极限写于正上正下的极限运算：
$\displaystyle_{写于下部的变量极限}^{写于上部的变量极限}$，如$\displaystyle \lim_{x\to0}^{y\to\infty}$显示为： lim x → 0 y → ∞ \displaystyle \lim_{x\to0}^{y\to\infty} x→0limy→∞ - 积分运算：
∫
写于下部的变量极限
写于上部的变量极限
表达式
d
x
\int_{写于下部的变量极限}^{写于上部的变量极限}表达式dx
∫写于下部的变量极限写于上部的变量极限表达式dx，如
$\int_{x\to 0}^{\infty}xdx$，显示为： ∫ x → 0 ∞ x d x \int_{x\to 0}^{\infty}xdx ∫x→0∞xdx - 将变量极限写于正上正下的积分运算：在
\int前加\displaystyle。如$\displaystyle \int_{x\to 0}^{\infty}xdx$，显示为： ∫ x → 0 ∞ x d x \displaystyle \int_{x\to 0}^{\infty}xdx ∫x→0∞xdx - 求和运算：
∑
写于下部的变量极限
写于上部的变量极限
表达式
\sum_{写于下部的变量极限}^{写于上部的变量极限}表达式
∑写于下部的变量极限写于上部的变量极限表达式，如
$\sum_{x=0}^{\infty}x$，显示为： ∑ x = 0 ∞ x \sum_{x=0}^{\infty}x ∑x=0∞x - 将变量极限写于正上正下的求和运算：在
\sum前加\displaystyle。如$\displaystyle \sum_{x=0}^{\infty}x$，显示为： ∑ x = 0 ∞ x \displaystyle \sum_{x= 0}^{\infty}x x=0∑∞x - 多个变量条件的求和运算
$\sum_{上位公式 \atop 下位公式}$, 如$\sum_{i=0\atop j=0}^{i=n\atop j=n}i+j$∑ i = 0 j = 0 i = n j = n ( i + j ) \displaystyle\sum_{i=0\atop j=0}^{i=n\atop j=n}(i+j) j=0i=0∑j=ni=n(i+j) - 微分
-
- 常微分
-
-
- 一阶常微分
$\mathrm{d}x$显示为： d x \mathrm{d}x dx
点微分（导数）$\dot x$显示为： x ˙ \dot x x˙
- 一阶常微分
-
-
-
- 二阶常微分
$\ddot x$显示为： x ¨ \ddot x x¨
- 二阶常微分
-
-
-
-
n
n
n 阶常微分
$x^{(n)}$显示为： x ( n ) x^{(n)} x(n)
-
n
n
n 阶常微分
-
-
- 偏微分
-
-
- 一阶偏微分
$\partialx$显示为： ∂ x \partial x ∂x
- 一阶偏微分
-
-
-
-
n
n
n 阶偏微分
$\partial^nx$显示为： ∂ n x \partial^nx ∂nx
-
n
n
n 阶偏微分
-
-
- 梯度
$\nabla$∇ \nabla ∇
- 梯度
逻辑符号
- 不等于：
$\neq$， ≠ \neq = - 大于等于：
$\geq$， ≥ \geq ≥ - 不大于等于：
$\ngeq$， ≱ \ngeq ≱；$\notgeq$， ≱ \not\geq ≥ - 小于等于：
$\leq$， ≤ \leq ≤ - 不小于等于：
$\nleq$， ≰ \nleq ≰；$\notleq$， ≰ \not\leq ≤ - 约等于：
$\approx$≈ \approx ≈ - 恒定等于：
$\equiv$≡ \equiv ≡
集合运算
- 属于运算
$\in$∈ \in ∈ - 不属于运算
$\notin$ 或 $\not\in∉ \notin ∈/ - 子集运算
$\subset$⊂ \subset ⊂;$\supset$⊃ \supset ⊃ - 非子集运算
$\not\subset$⊄ \not\subset ⊂;$\not\supset$⊅ \not\supset ⊃ - 真子集运算
$\subseteq$⊆ \subseteq ⊆;$\supseteq$⊇ \supseteq ⊇ - 非真子集运算
$\subsetneq$⊊ \subsetneq ⊊;$\supsetneq$⊋ \supsetneq ⊋ - 交集
$\cap$∩ \cap ∩ - 并集
$\cup$∪ \cup ∪ - 差集
$\setminus$∖ \setminus ∖ - 同或
$\bigodot$⨀ \bigodot ⨀ - 同与
$\bigotimes$⨂ \bigotimes ⨂ - 空集
$\emptyset$∅ \emptyset ∅
特殊符号
$\infty$∞ \infty ∞$\hat{a}$a ^ \hat{a} a^$\check{a}$a ˇ \check{a} aˇ$\breve{a}$a ˘ \breve{a} a˘$\tilde{a}$a ~ \tilde{a} a~$\bar{a}$a ˉ \bar{a} aˉ$\vec{a}$a ⃗ \vec{a} a$\acute{a}$a ˊ \acute{a} aˊ$\grave{a}$a ˋ \grave{a} aˋ$\mathring{a}$a ˚ \mathring{a} a˚$\uparrow$↑ \uparrow ↑$\Uparrow$⇑ \Uparrow ⇑$\downarrow$↓ \downarrow ↓$\Downarrow$⇓ \Downarrow ⇓$\leftarrow$← \leftarrow ←$\Leftarrow$⇐ \Leftarrow ⇐$\rightarrow$→ \rightarrow →$\Rightarrow$⇒ \Rightarrow ⇒
箭头大全摘抄自清辉万里----Markdown箭头的输入方法汇总
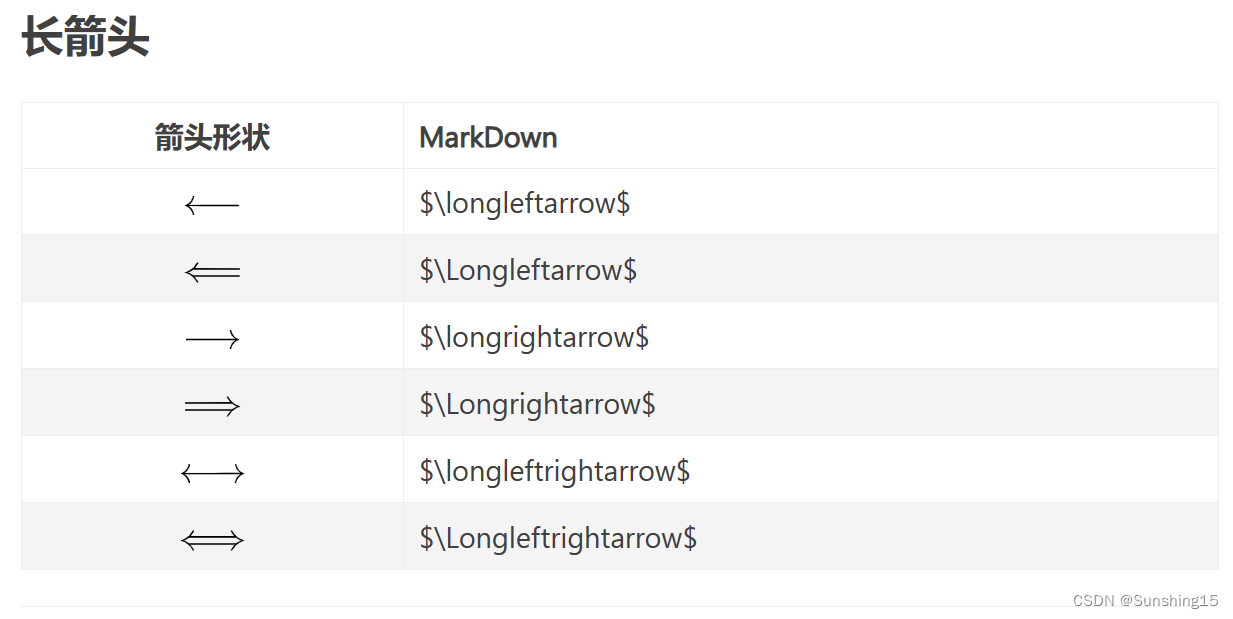
参考文献
[1]箭头大全
扫一扫
1082
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
