统筹学问题

七桥问题

• 凡是由偶点组成的连通图，一定可以一笔画成。画时可以把任一偶点为起点，最后一定能以这个点为终点画完此图。
• 凡是只有两个奇点的连通图(其余都为偶点)，一定可以一笔画成。画时必须把一个奇点为起点，另一个奇点为终点。
• 其他情况的图都不能一笔画出。（奇点数除以2便可算出此图需几笔画成。）

线性规划

例题：某乳制品加工厂用纯牛奶和酸牛奶两种生产原料，加工生产甲、乙两种乳制品、该厂加工每单位乳制品消耗原料数、每单位乳制品的利润如下所示。则该公司的最大利润为( 1）万元。公司获得最大利润时，生产甲的数量是（2）吨。
(1)A.140        B.144        C.175        D.178
(2)A.5            B.6            C.40          D.50

		甲	乙	现有原料（吨）
原料（吨）	纯牛奶	1	2	86
	酸牛奶	5	3	150
利润（万元）		3	4

【解析】假设甲乳制品生产的数量是X吨，乙乳制品生产的数量是Y吨。
根据题干可以得到：不等式1：X+2Y≤86，不等式2：5X+3Y≤150;
采取消元法，我们求得X=6，Y=40，可以使得该公司的最大利润=6×3+40×4=178(万元)，这个时候生产甲乳制品生产的数量是6吨。
【参考答案】(1)D；(2)B

图论

例题：下图为某地区的通信线路图，图中节点为8个城市，节点间标识的数字为城市间拟铺设通信线路的长度，为了保持8个城市通信连接，则至少铺设（ ) km的线路。
A.1000        B.1100        C.1200        D.1300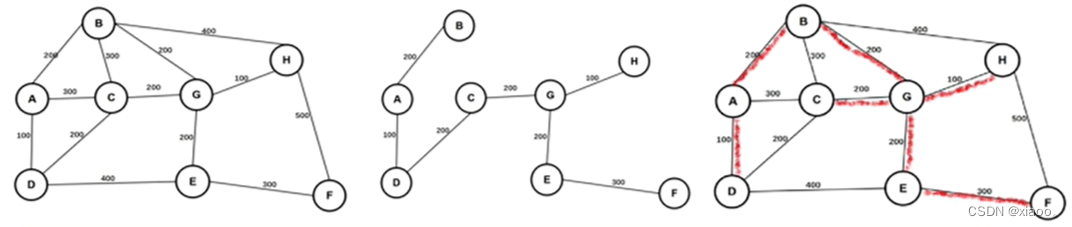
【解析】︰先断开最大的，然后保留最小和次小的，接着再断开次小的，以此类推。最终保证8个城市的通信处于连接。
最终计算结果，200+100+200+200+100+200+300=1 300 (km)
【参考答案】D

决策论

不确定型决策分析

        乐观决策准则、悲观决策准则、折中决策准则、后悔值决策准则、等概率决策准则。

• 最大最大(max-max)准则∶最大最大准则也称乐观准则，它找出每种行动的最好结果，再从最好结果中找一个更好的做为选择。
• 最大最小(max-min）准则∶最大最小准则也称悲观准则，也叫小中取大，它找出每种行动的最坏结果，再从最坏结果中找一个最好的做为它的选择。
• 最小机会损失准则（min-max）也称最小最大后悔准则，它利用机会成本的概念来进行决策。决策首先要计算机会损失（后悔值）矩阵；机会损失的概念是，当一个事件发生时，由于你没有选择最优决策而带来的收入损失。

最小最大后悔值法∶也称萨凡奇决策准确性准则，决策者不知道各种自然状态中任一种发生的概率，决策目标是确保避免较大的机会损失。运用最小最大后悔值法时，首先要将决策矩阵从利益矩阵转变成机会损失矩阵；然后确定每一可选方案的最大机会损失；再次，在这些方案的最大机会损失中，选出一个最小值，与该最小值对应的可选方案便是决策选择的方案。

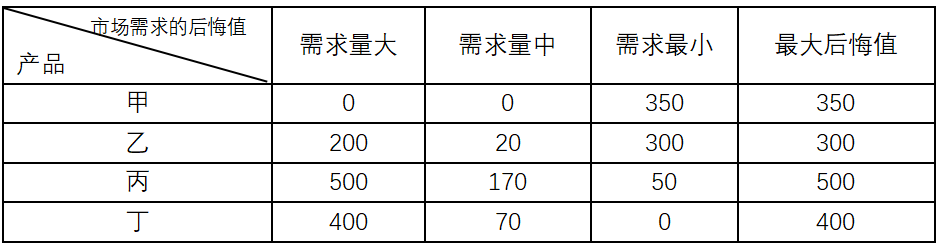
例题：某公司为经营业务的需要，决定要在现有生产条件不变的情况下生产一种新产品，现可供生产的产品有甲、乙、丙、丁四种类型。由于缺少相关资料背景，对新产品的市场需求，只能估计为大中小三种状态。在不同的市场需求条件下，新产品的收益值如表所示。如果决策者采用后悔值方法进行决策，该公司应生产（  ）。
A.甲        B.乙        C.丙        D.丁

【解析】：后悔值是每个状态的最大收益值作为理想目标，并将其他值与最大值相减所得差 作为未达到理想目标的后悔值。最后，按照最大后悔值达到最小的方法进行决策，因此也称为最小最 大后悔值。从本题看，各种状态的后悔值如下表所示： 根据上表所示，甲的最大后悔值为350，乙的最大后悔值为300，丙的最大后悔值为500，丁的 最大后悔值为400，最小值为乙的300。因此，选乙生产。

风险决策的灵敏度分析

灵敏度分析的要求：

• 通常，自然状态概率和条件损益值是不容易估计准确的，从而期望损益值也就不十分准确，因此有必要对状态或条件损益值数据的变动是否影响最优方案的选择进行分析。这种分析叫做灵敏度分析。如果最优方案对这些数据变动的反应是不敏感的，这样决策可靠性就比较大，决策错误的可能性就会比较小。

例题：某公司主营产品有甲、乙、丙、丁四种。按照历史数据预测，下半年的市场需求总量可能有10万件、15万件和20万件三种情况，对应的概率分别为50%、30%、20%。不同情况下各产品带来的市场收益(单位:万元)如表所示。为了追求利益最大化，该公司应该生成产（) 。
A.甲        B.乙        C.丙        D.丁

产品	需求量为10万件	需求量为15万件	需求量为20万件
甲	-25	35	70
乙	-20	30	65
丙	-10	25	55
丁	10	25	40

【解析】：
甲：EMV= (-25×50%) +(35×30%)+ (70×20%)=12
乙：EMV= (-20×50%) +(30×30%) +(65×20%)=12
丙：EMV=(-10×50%) +(25×30%)+(55×20%)=13.5
丁：EMV= (10×50%) +(15×30%)+ (40×20%)=17.5
因为要追求利益最大化,丁的EMV最大，因此选D。
【参考答案】：D