本文详细介绍了FP16格式的工作原理，包括如何通过这种格式表示十进制小数，以及如何在Verilog中实现FP16加法器和乘法器的实现过程，涉及阶数调整、尾数操作和规格化处理。
1.关于FP16格式的理解
首先，一个十进制数可写成一个纯小数乘上10的若干次方，类似的，一个二进制数可写成一个纯小数乘上2的若干次方。一般地,任一个二进制N，可表示为N=f x 2^(e)。f代表二进制的小数（fraction），e带表阶数(exponent)，故人们用如下格式保存FP16和FP32：
2.如何通过FP16格式计算出它表示的十进制小数
FP16: 
FP32: 
先放上公式，再来解释人们为什么这样定义公式。
首先第一个问题：人们为什么需要exponent减15或者减127？因为只有这样，才可以计算出2的负次幂，减去的这个数称为‘’偏置常数‘’，它等于2^(n-1)-1,其中n为exponent的位数，
故2^(5-1)-1=15, 2^(8-1)-1=127
其次第二个问题：公式里面的1.fraction的这个“1”是怎么来的？因为fraction最高位的再高一位被称为隐藏位，这个隐藏位就固定是“1”。举个例子更好理解：已知十进制的0.75用FP32可以表示为0_01111110_10…0，(省略号表示都是0)，那还有没有其它的表示方法呢?当然有啦！就好比在十进制中0.75可以写成75x10^(-2)也可以写成7.5x10^(-1)，0.75用FP32还可以表示成
0_10000101_0000001100…0，可以看出0.75的阶数增加了7(133-126=7)，故尾数右移7位，隐藏位就显现出来了，当中尾数多出来的1便是隐藏位。所以这个隐藏位1在公式中其实是可有可无的。
3.Verilog实现FP16加法器乘法器
加法器：1.对阶，将两个小数的exponent化为相同的；2.尾数相加；3.化为FP16标准；
module floatAdd (floatA,floatB,sum);
input [15:0] floatA, floatB;
output reg [15:0] sum;
reg sign;
reg signed [5:0] exponent; //fifth bit is sign
reg [9:0] mantissa;
reg [4:0] exponentA, exponentB;
reg [10:0] fractionA, fractionB, fraction; //fraction = {1,mantissa}
reg [7:0] shiftAmount;
reg cout;
always @ (floatA or floatB) begin
exponentA = floatA[14:10];
exponentB = floatB[14:10];
fractionA = {1'b1,floatA[9:0]};//将隐藏位表示出来进行计算
fractionB = {1'b1,floatB[9:0]}; //同理
exponent = exponentA;
if (floatA == 0) begin //special case (floatA = 0)
sum = floatB;
end else if (floatB == 0) begin //special case (floatB = 0)
sum = floatA;
end else if (floatA[14:0] == floatB[14:0] && floatA[15]^floatB[15]==1'b1) begin
sum=0;
end else begin
if (exponentB > exponentA) begin//对阶：将阶数(exponent)化为相同的，小阶化为大阶。好比6.6x10^(6)和8.8x10^(4)相加时，我们会化成6.6x10^(6)和0.088x10^(6)进行运算
shiftAmount = exponentB - exponentA;
fractionA = fractionA >> (shiftAmount);//要将floatA化为大阶，则尾数要右移，尾数减小
exponent = exponentB;
end else if (exponentA > exponentB) begin //同理
shiftAmount = exponentA - exponentB;
fractionB = fractionB >> (shiftAmount);
exponent = exponentA;
end
if (floatA[15] == floatB[15]) begin //same sign
{cout,fraction} = fractionA + fractionB;
if (cout == 1'b1) begin//‘相加后的值’的小数点前的第二位如果是1，则要向右移一位，确保小数点前只有一位
{cout,fraction} = {cout,fraction} >> 1;
exponent = exponent + 1;
end
sign = floatA[15];
end else begin //different signs
if (floatA[15] == 1'b1) begin
{cout,fraction} = fractionB - fractionA;//如果B比A小，则相减后得到补码，cout为符号位
end else begin
{cout,fraction} = fractionA - fractionB;//同理
end
sign = cout;
if (cout == 1'b1) begin
fraction = -fraction;//将补码转化为原码
end else begin
end
if (fraction [10] == 0) begin
if (fraction[9] == 1'b1) begin//规格化，将隐藏位再次隐藏起来
fraction = fraction << 1;
exponent = exponent - 1;
end else if (fraction[8] == 1'b1) begin
fraction = fraction << 2;
exponent = exponent - 2;
end else if (fraction[7] == 1'b1) begin
fraction = fraction << 3;
exponent = exponent - 3;
end else if (fraction[6] == 1'b1) begin
fraction = fraction << 4;
exponent = exponent - 4;
end else if (fraction[5] == 1'b1) begin
fraction = fraction << 5;
exponent = exponent - 5;
end else if (fraction[4] == 1'b1) begin
fraction = fraction << 6;
exponent = exponent - 6;
end else if (fraction[3] == 1'b1) begin
fraction = fraction << 7;
exponent = exponent - 7;
end else if (fraction[2] == 1'b1) begin
fraction = fraction << 8;
exponent = exponent - 8;
end else if (fraction[1] == 1'b1) begin
fraction = fraction << 9;
exponent = exponent - 9;
end else if (fraction[0] == 1'b1) begin
fraction = fraction << 10;
exponent = exponent - 10;
end
end
end
mantissa = fraction[9:0];//
if(exponent[5]==1'b1) begin //exponent is negative：1.exponent太大了溢出；2.规格化后发现exponent太小了，忽略，直接等于0
sum = 16'b0000000000000000;
end
else begin
sum = {sign,exponent[4:0],mantissa};
end
end
end
endmodule补充解释：
fractionA = {1'b1,floatA[9:0]};
fractionB = {1'b1,floatB[9:0]};
//很多人把这里理解为‘借位’，但我不这么认为，如果是借位不应该是{1'b1,floatA[9:1]}吗？并且此处代码exponent的值也没有加减代码中将隐藏位显示出来计算，就好比两个公式相加：
在化为同阶后，相当于两个11bit的二进制数相加，所以最大可以得到一个12bit的数：
如图在相加得到的12bit中，小数点的位置也一定是确定的，所以如下代码中，我们进行右移位，让cout一定为0：
if (cout == 1'b1)
begin
{cout,fraction} = {cout,fraction} >> 1;
exponent = exponent + 1;
end所以，最后要再将隐藏位再藏起来时（规格化），如果f[10]=1，那么就直接取f[0:9]即可，此时f[10]为新的隐藏位。如果f[9]=1，则f向左移一位，此时f[9]为新的隐藏位，相当于小数点向右移一位，所以exponent减一，之后以此类推。
波形验证：
乘法器：1.阶数相加；2.尾数相乘；3.化为FP16标准；
module floatMult (floatA,floatB,product);
input [15:0] floatA, floatB;
output reg [15:0] product;
reg sign;
reg signed [5:0] exponent; //6th bit is the sign
reg [9:0] mantissa;
reg [10:0] fractionA, fractionB; //fraction = {1,mantissa}
reg [21:0] fraction;
always @ (floatA or floatB) begin
if (floatA == 0 || floatB == 0) begin
product = 0;
end else begin
sign = floatA[15] ^ floatB[15];//异或，相异为1
exponent = floatA[14:10] + floatB[14:10] - 5'd15 ;
fractionA = {1'b1,floatA[9:0]};//显示出隐藏位1来计算
fractionB = {1'b1,floatB[9:0]};
fraction = fractionA * fractionB;
if (fraction[21] == 1'b1) begin//规格化，将隐藏位再次隐藏起来
fraction = fraction << 1;
exponent = exponent + 1;
end else if (fraction[20] == 1'b1) begin
fraction = fraction << 2;
exponent = exponent + 0;
end else if (fraction[19] == 1'b1) begin
fraction = fraction << 3;
exponent = exponent - 1;
end else if (fraction[18] == 1'b1) begin
fraction = fraction << 4;
exponent = exponent - 2;
end else if (fraction[17] == 1'b1) begin
fraction = fraction << 5;
exponent = exponent - 3;
end else if (fraction[16] == 1'b1) begin
fraction = fraction << 6;
exponent = exponent - 4;
end else if (fraction[15] == 1'b1) begin
fraction = fraction << 7;
exponent = exponent - 5;
end else if (fraction[14] == 1'b1) begin
fraction = fraction << 8;
exponent = exponent - 6;
end else if (fraction[13] == 1'b1) begin
fraction = fraction << 9;
exponent = exponent - 7;
end else if (fraction[12] == 1'b0) begin
fraction = fraction << 10;
exponent = exponent - 8;
end
mantissa = fraction[21:12];
if(exponent[5]==1'b1) begin //exponent is negative 1.exponent太大了溢出；2.exponent太小了，忽略，直接等于0
product=16'b0000000000000000;
end
else begin
product = {sign,exponent[4:0],mantissa};
end
end
end
endmodule
补充解释：
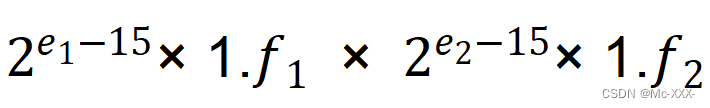
如图在相乘得到的22bit中，小数点的位置也一定是确定的。
所以，最后要再将隐藏位再藏起来时，如果f[21]=1，则f向左移一位，此时f[21]为新的隐藏位，相当于小数点向左移一位，所以exponent加一，之后以此类推。
波形验证：
扫一扫
814
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
