优化方法理论合集（1）——最简单问题

1. 问题背景

首先来看如何定义一个最优化问题。
一个最优化问题不可或缺4个条件：

1. 优化器，在系统中起到优化的作用。
2. 数学模型。系统的数学模型一般可以用以下形式描述：
   $$\{\begin{array}{l}{\dot{x}}_1=f_1\left(t,\vec{x},\vec{u}\right)\\ {\dot{x}}_2=f_2\left(t,\vec{x},\vec{u}\right)\\ ⋮\\ {\dot{x}}_m=f_n\left(t,\vec{x},\vec{u}\right)\end{array}$$此种形式称为柯西形式。
3. 性能指标，一般记为$J$，它表征了以何种方式来衡量优化的程度。
   一般地，性能指标$J$还可以具有以下3种形式：
   3.1) 拉格朗日形式：
   $$J={\int }_{t_0}^{t_k}F\left(t,\vec{x},\dot{\vec{x}},\vec{u}\right)dt\to extr.,t\in \left[t_0,t_k\right]$$其中$ertr$表示$J$趋于极值；$F$为被积函数。
   值得注意的是，整个积分部分${\int }_{t_0}^{t_k}Fdt$被称为泛函数。
   拉格朗日形式最常见，多体现在对快速性有要求的系统中。如，对时间有要求（一般要求时间最短）的任务中就有
   $$J={\int }_{t_0}^{t_k}1dt=t_k-t_0=\Delta t\to min$$
   3.2) 迈耶尔形式：
   $$J=\Phi \left(\vec{x}\left(t_0\right),\vec{x}\left(t_k\right)\right)\to extr.$$此种形式不是积分型的，因此称为端点型，仅取决于$x(t_0)$与$x(t_k)$两个边界值。
   3.3) 波尔茨型：
   $$J={\int }_{t_0}^{t_k}F\left(t,\vec{x},\dot{\vec{x}},\vec{u}\right)dt+\Phi \left[x(t_0),x(t_k)\right]\to extr.$$这种形式是拉格朗日型和迈耶尔型的组合形式，既含有积分项，也含有端点项。
4. 优化算法。这一部分即为重点部分，将在本次及后续笔记分享中逐一介绍。

2. 最简单问题

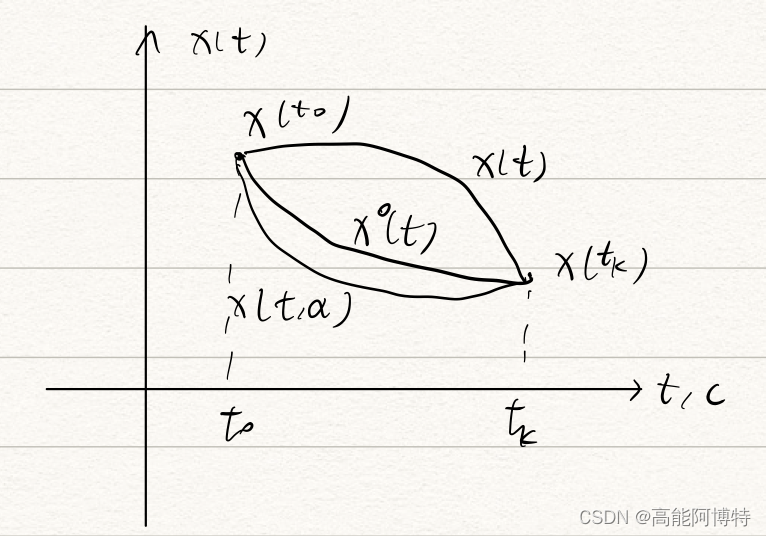
如上图所示，设$x^{\circ }(t)$为最优轨迹，起点为$x(t_0)$，终点为$x(t_k)$。任务目标是寻找一条最优路径，从$x(t_0)$出发，到$x(t_k)$截止（即穿过两点），并满足一定的其他要求或约束。

在寻找该最优路径的过程中，可能得到很多条连接起点和终点的轨迹，它们统称为曲线簇，具有以下形式：
$$x(t)=x^{\circ }(t)+\alpha \cdot \delta x(t)\text{\hspace{1em}(1)}$$其中$\delta x(t)$是该最优轨迹的变分。
(1)式可以这样理解：所得到的曲线簇是在最优轨迹$x^{\circ }(t)$基础上，进行不同程度的偏离得到的，偏移量即为变分$\delta x(t)$。随着$\alpha$取值不同，偏移量也不同，进而构成了一组曲线簇集合，而$x^{\circ }(t)$正是其中最优的一条。

3. 欧拉公式

这里不加证明地引入欧拉公式：
$$F_x-\frac{d}{dt}{F}_{\dot{x}}=0\text{\hspace{1em}(2)}$$其中$F_x$为$F$关于$x$的导数，$F_{\dot{x}}$为$F$关于$\dot{x}$的导数。
欧拉方程是$J$的极值存在的必要但非充分条件。

4. 具体算法步骤

下面列出最简单问题的具体算法步骤。

1. 列出条件，包含如下部分：
   1-1) 时间区间$t\in \left[t_0,t_k\right]$；
   1-2) 边界条件$x(t_0),x(t_k)$共2个；
   1-3) 拉格朗日判据：
   $$J={\int }_{t_0}^{t_k}F\left(t,x,\dot{x}\right)dt\to extr.$$以上三点也是最简单问题不可或缺的3个条件，缺一不可。
2. 算出偏导数，为欧拉方程做准备：
   $$\begin{array}{rl}{F}_x& =\frac{\partial F}{\partial x}\\ F_{\dot{x}}& =\frac{\partial F}{\partial \dot{x}}\end{array}$$
3. 写出欧拉方程：
   $$F_x-\frac{d}{dt}{F}_{\dot{x}}=0$$
4. 用两个边界条件解欧拉方程。它是二阶微分方程，有唯一解。
5. 证明解的唯一性。

5. 例题

设性能指标为
$$J={\int }_0^1\left(x^2+{\tau }^2{\dot{x}}^2\right)dt\to extr.$$边界条件：
$$\{\begin{array}{l}x(0)=0\\ x(1)=x_1\end{array}$$时间区间：
$$t\in \left[0,1\right]$$要求找出最优的$x^{\circ }(t)$。

解：

1. $F\left(t,x,\dot{x}\right)=x^2+{\tau }^2{\dot{x}}^2$。
2. 计算欧拉方程：
   $$\begin{array}{rl}{F}_x& =\frac{\partial F}{\partial x}=2x\\ F_{\dot{x}}& =\frac{\partial F}{\partial \dot{x}}=2{\tau }^2\dot{x}\end{array}$$代入欧拉方程
   $$F_x-\frac{d}{dt}{F}_{\dot{x}}=0⟹2x-2{\tau }^2\ddot{x}=0$$解得
   $$x(t)=C_1{e}^{\frac{1}{\tau }t}+C_2{e}^{-\frac{1}{\tau }t}\text{\hspace{1em}(1)}$$由于$C$取值不定，因此(1)式即为一组曲线簇。
   为了确定$C$，需要代入边界条件：
   $$x(0)=0,x(1)=x_1$$解出
   $$\{\begin{array}{ll}{C}_1& =\frac{x_1}{e^{\frac{1}{\tau }-e^{-\frac{1}{\tau }}}}\\ C_2& =-\frac{x_1}{e^{\frac{1}{\tau }-e^{-\frac{1}{\tau }}}}\end{array}$$那么就可以得到最优解
   $$x^{\circ }(t)=\frac{x_1}{e^{\frac{1}{\tau }-e^{-\frac{1}{\tau }}}}{e}^{\frac{1}{\tau }t}-\frac{x_1}{e^{\frac{1}{\tau }-e^{-\frac{1}{\tau }}}}{e}^{-\frac{1}{\tau }t}$$
   之前提到过，欧拉方程仅仅是必要条件，只能保证已经达到极值，但并不能指出是最大值还是最小值。因此，这里附加一个条件进行判别，称为拉格朗日条件：
   若$F_{\dot{x}\dot{x}}=\frac{{\partial }^{2}F}{\partial {\dot{x}}^2}<0$，则$J\to max$；
   若$F_{\dot{x}\dot{x}}=\frac{{\partial }^{2}F}{\partial {\dot{x}}^2}>0$，则$J\to min$；
   若$F_{\dot{x}\dot{x}}=0$，那么要么是欧拉方程解错了，要么是存在断点/不连续点。

6. 最简单问题的几种情形

1. $F(x,t)$，即$F$中不含有$\dot{x}$。此时欧拉方程变为
   $$F_x=0$$
2. $F\left(\dot{x},t\right)$，即$F$中不含$x$。此时欧拉方程变为
   $$\frac{d}{dt}{F}_{\dot{x}}=0$$即
   $$F_{\dot{x}}=const.$$
3. $F\left(x,\dot{x}\right)$中不含$t$。此时欧拉方程变为
   $$F-\dot{x}{F}_{\dot{x}}=const.$$