交叉熵损失函数，KL散度， Focal loss

置顶 Tiny番茄

已于 2025-05-17 11:40:19 修改

阅读量739

点赞数 15

文章标签：机器学习人工智能

于 2025-05-16 23:36:34 首次发布

本文链接：https://blog.csdn.net/weixin_59234335/article/details/148018924

版权

交叉熵损失函数（Cross-Entropy Loss）

二分类交叉熵

多分类交叉熵

KL散度（Kullback-Leibler Divergence)

交叉熵损失函数和KL散度总结

Focal loss

Focal loss 和交叉熵损失函数的区别

交叉熵损失函数（Cross-Entropy Loss）

交叉熵损失函数，涉及两个概念，一个是损失函数，一个是交叉熵。

首先，对于损失函数。在机器学习中，损失函数就是用来衡量我们模型的预测结果与真实结果之间“差距”的函数。这个差距越小，说明模型的表现越好；差距越大，说明模型表现越差。我们训练模型的目标，就是通过不断调整模型的参数，来最小化这个损失函数。以一个生活化的例子举例，想象一下你在教一个孩子识别猫和狗。孩子每次猜对或猜错，你都会给他一个“评分”。如果他猜对了，评分就很高（损失很小）；如果他猜错了，评分就可能很低（损失很大）。

在明白完损失函数后，就要理解交叉熵了，在理解交叉熵之前我们又要了解何为熵。熵在信息论中是衡量一个随机变量不确定性（或者说信息量）的度量。不确定性越大，熵就越大。根据信息论中的香农定理，我们可以得出熵的计算公式为：

其中，P(xi)是事件xi发生的概率。- log(P(xi)) 表示信息量，根据公式我们可以知道信息量大小与概率成负相关，概率越小的时间其信息量越大，如飞机失事；概率越大的时间其信息量越小，如太阳从东边升起。

谈完熵之后，我们来开始理解何为交叉熵？

交叉熵是衡量两个概率分布之间“相似性”的度量。更准确地说，它衡量的是，当我们使用一个非真实的概率分布 Q 来表示一个真实的概率分布 P 时，所需要付出的“代价”或“信息量”。交叉熵的计算公式为：

注意，这里的 P(xi) 通常是one-hot编码形式，即在分类问题中，只有真实类别对应的 P(xi) 为1，其他为0。

二分类交叉熵

在二分类问题中，当你的模型需要判断一个输入是A类还是B类（比如是猫还是狗，是垃圾邮件还是正常邮件）时，你会使用二分类交叉熵。

真实标签 (y)：通常用0或1表示。例如，猫是1，狗是0。
模型预测概率 ( $\widehat{y}$ )：模型输出的属于类别1的概率，通常通过Sigmoid激活函数得到，范围在0到1之间。

二分类交叉熵公式为：

直观理解：

如果真实标签 y=1（比如是猫）：损失函数变为 −log( $\widehat{y}$ )。此时，如果 $\widehat{y}$ 接近1（模型预测是猫的概率很高），log( $\widehat{y}$ ) 就接近0，损失就小；如果 $\widehat{y}$ 接近0（模型预测是猫的概率很低），log( $\widehat{y}$ ) 就变成一个很大的负数，损失就大。
如果真实标签 y=0（比如是狗）：损失函数变为 −log(1− $\widehat{y}$ )。此时，如果 $\widehat{y}$ 接近0（模型预测是狗的概率很高），1− $\widehat{y}$ 接近1，log(1− $\widehat{y}$ ) 接近0，损失就小；如果 $\widehat{y}$ 接近1（模型预测是狗的概率很低），1− $\widehat{y}$ 接近0，log(1− $\widehat{y}$ ) 变成一个很大的负数，损失就大。

多分类交叉熵

当你的模型需要判断一个输入是N个类别中的哪一个（比如是猫、狗、还是鸟）时，你会使用多分类交叉熵。

真实标签 (y)：通常是one-hot编码。例如，猫是 [1,0,0]，狗是 [0,1,0]，鸟是 [0,0,1]。
模型预测概率 ( $\widehat{y}$ )：模型输出的属于每个类别的概率分布，通常通过Softmax激活函数得到，所有概率之和为1。

多分类交叉熵的公式为：

其中，N 是类别的数量，yi 是真实标签中第 i 个类别的指示（0或1）， $\widehat{y}$ i 是模型预测第 i 个类别的概率。

直观理解：

由于真实标签 y 是one-hot编码，只有真实类别 k 对应的 yk 是1，其他 yi 都是0。所以，这个求和公式实际上只计算了真实类别对应的预测概率的负对数。
举例：如果真实标签是猫 [1,0,0]，模型预测是 [0.8(猫),0.1(狗),0.1(鸟)]。损失 =−(1⋅log(0.8)+0⋅log(0.1)+0⋅log(0.1))=−log(0.8)。如果模型预测是 [0.1(猫),0.8(狗),0.1(鸟)]。损失 =−(1⋅log(0.1)+0⋅log(0.8)+0⋅log(0.1))=−log(0.1)。显然，−log(0.1) 比 −log(0.8) 要大很多，说明模型预测猫的概率很低时，损失会很大，这符合我们的直觉。

KL散度（Kullback-Leibler Divergence)

KL散度和交叉熵很像，只不过交叉熵是硬标签，KL散度是软标签，因此KL散度也称为相对熵，是衡量两个概率分布 P 和 Q 之间差异的非对称度量。它量化了当使用概率分布 Q 来近似概率分布 P 时所损失的信息量。KL散度主要用于拉近真实分布和近似分布的表达，去让近似分布尽可能接近真实分布，因为越近似，其除法越近于1，log()越接近于0。其计算公式为：

其中，P为真实分布，Q为近似分布。我们将其展开，可得到以下公式：

可以看到当P(xi)为1时，这时就变成交叉熵了。

KL散度特性

非负性（涉及数学的非负性证明）：KL(P∣∣Q)≥0（因为P和Q不相等的话，即P/Q>1），只有当 P 和 Q 是完全相同的分布时（此时P/Q = 1），KL(P∣∣Q)=0。
非对称性：KL(P∣∣Q) 不等于 KL(Q∣∣P) 。KL(P∣∣Q)是惩罚 Q 在 P 概率高的地方给出低概率。KL(Q∣∣P)惩罚 Q 在 P 概率低的地方给出高概率。
度量的是“信息损失”：它衡量的是当你用 Q 来编码 P 时，额外需要多少比特的信息。

交叉熵损失函数和KL散度总结

交叉熵损失函数适用于分类任务，基于硬标签，目的是衡量模型预测的概率分布与真实标签的概率分布之间的“距离”。它的目标是让模型对真实类别的预测概率尽可能高。
KL散度适用于衡量两个概率分布之间的差异，是非对称的，多用于概率模型，用于强制模型学习到的分布与某个先验分布接近，或衡量两个复杂分布之间的相似性。

Focal loss

Focal Loss 是一种专门设计用于处理类别不平衡问题的损失函数，特别是在CV中目标检测任务中表现出色。

为什么提出Focal loss？

在许多实际应用中，如目标检测，类别不平衡是一个常见问题。例如，在一个图像中，背景（负样本）通常占据大多数，而目标物体（正样本）很少。如果采用传统的交叉熵损失则会导致模型过度关注负样本，从而忽视正样本。

那现在就有个疑问，交叉熵损失也可为类别分配权重比，分配权重比不就可以了吗？

分配权重比确实有助于提高正样本的关注程度，但交叉熵损失函数无法让模型去具体地关注简单和困难样本，而在目标检测中，由于存在较多作为背景的负样本，因此作为目标物体的正样本在预测中被预测为正样本的概率较小，因此如果能从困难样本的角度出发的话，当被预测为正确且概率较大时，对应的loss应较小，而当被预测为正确且概率较小时，对应的loss应较大，这样的话，就起到了对困难样本的关注作用。而Focal Loss 旨在通过将注意力集中在难以分类的样本上，通过一个平衡因子和一个焦点因子来对交叉熵损失函数进行优化。

Focal loss 定义

Focal loss 的公式如下

$p_t$ 是模型对目标类的预测概率
$\alpha_t$ 是平衡因子，用于调整正负样本之间的影响
$\gamma$ 是焦点因子，用于调整难易样本的权重

其中， $\alpha_t$ 用于平衡正负样本的影响，防止负样本过多对损失的贡献。

假如，对于负样本 $\alpha_t$ = $\alpha$ 的话，那正样本 $\alpha_t$ = $1-\alpha$ 。 $\alpha$ 的值在[0,1]，表示正负样本的权重比例。如果负样本占比4/5，正样本占比1/5的话，那 $\alpha$ 可以设置为0.2，这样的话负样本在损失计算中的占比就下降了，正样本的得到了突出，二者不平衡的关系在loss计算中达成1:1的平衡关系（负样本：0.8*0.2 = 正样本 0.2*0.8）。当然这种也不一定是这么设置，在Focal loss原论文中，负样本和正样本占比约为1000:1，但实验显示是当给正样本权重为0.2时，效果最好，因此权重的分配也要看具体任务，或者网格化搜索来确定最佳参数。

焦点因子 $\gamma$ 用于调整简单和困难样本在损失中的贡献，是基于幂计算来进行调整的。具体地，

当预测概率 $p_t$ 接近1时，即样本容易分类，那么 1 - $p_t$ 就会小，而一个小于1的进行大于1的幂计算后只会变得更小，因此 $(1 - p_t)^{\gamma }$ 会非常小，从而降低了简单分类样本在损失中的贡献
当预测概率 $p_t$ 接近0时，即样本难以分类，那么 1 - $p_t$ 就会大，而一个小于1的进行大于1的幂计算后会变得更小，但由于1 - $p_t$ 较大，因此困难样本的 $(1 - p_t)^{\gamma }$ 相比简单样本来说会大不少，从而增加了困难分类样本在损失中的贡献

焦点因子 γ 通常设为2，但可以根据具体问题调整。更大的 γ会使得模型更加专注于难分类样本，但更大的 γ 也可能会进一步使得一些困难样本被划分为简单样本了，因此在参数上的选取也不是越大越好。

Focal loss 和交叉熵损失函数的区别

Focal loss是基于二分类的交叉熵进行优化的，现比较二者的区别。

交叉熵损失

其中， $p_t$ 是模型对正确类别的预测概率。

可以看到Focal loss与交叉熵的区别在于平衡因子和焦点因子的添加，但Focal loss重点还是在焦点因子的设计上且在这方面可解释性强，在权重因子上，交叉熵损失在具体实现的时候也能赋予不同样本的loss权重比。

下面是一个例子将说明焦点因子是如何聚焦在困难样本上的，并且探讨交叉熵和Focal loss的区别。

1. 对于一个简单样本，如预测一张图片没有猫。

那么真实标签y=0 (没有猫)
模型预测 p =0.01 (预测有猫的概率非常低，即预测没有猫的概率非常高)。这是一个“容易分类”的负样本，模型表现非常好。那么预测没有猫的概率就是p = 0.99，因此模型预测为与真实标签（没有猫）相同的概率是p = 0.99

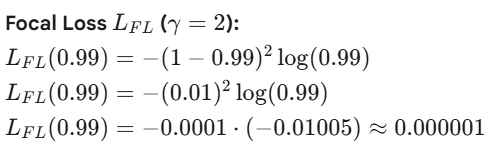
2.对于一个困难样本，如预测一张图片有猫

那么真实标签y=1（有猫）
如果模型预测p=0.1（预测有猫的概率非常低，即模型分类错误），这是一个难以分类的正样本，模型表现非常差。因此模型预测为与真实标签（有猫）相同的概率是p = 0.1

根据例子，我们可以得出以下结论

Focal loss可以有效衰减简单样本在loss中的表现，并且可以较好的保持困难样本的loss值，从而让模型关注困难样本的学习上，如上述例子中，困难样本的loss = 1.86，简单样本的loss = 0.000001，二者相差的数量级达 $10^7$ 。而在交叉熵损失中，困难样本loss = 2.30，简单样本的loss = 0.01，二者相差的数量级达 $10^2$ 。因此Focal loss可以有效关注到困难样本的loss贡献。