三维路径跟踪算法：三维LOS制导+PID艏向+PID纵倾跟踪控制（Matlab代码、Simulink仿真）

 💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

三维路径跟踪算法：三维LOS制导+PID艏向+PID纵倾跟踪控制研究

一、三维LOS制导算法的基本原理与改进

二、PID艏向与纵倾控制的实现方式

三、三维LOS制导与PID控制的协同策略

四、三维LOS与PID纵倾控制的耦合效应分析

五、多PID控制器的协调机制

六、研究趋势与挑战

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码、Simulink仿真

---

💥1 概述

三维路径跟踪算法：三维LOS制导+PID艏向+PID纵倾跟踪控制研究

---

一、三维LOS制导算法的基本原理与改进

1. 基本原理
   三维LOS（Line of Sight）制导是一种基于视线几何关系的导航方法，通过计算载体（如船舶、无人机）与目标点之间的航向角和仰角，生成期望的路径跟踪指令。其核心公式为：

改进策略

• 自适应看前距离：根据路径曲率和载体速度动态调整 ΔΔ，例如在路径拐点处减小 ΔΔ 以提高跟踪精度。

• 

三维扩展：将传统二维LOS扩展到三维，通过引入仰角控制垂向运动（如潜水器的深度跟踪），结合航向角和仰角实现三维路径跟踪

二、PID艏向与纵倾控制的实现方式

1. PID艏向控制

   • 传统PID的局限性：依赖固定数学模型，对海况变化（如风浪、载重波动）敏感，易出现积分饱和和超调。
   • 改进方案：
     • 模糊PID：利用模糊逻辑动态调整PID参数（Kp,Ki,KdKp​,Ki​,Kd​），根据航向偏差及变化率实时优化控制输出。
     • 滑模PID：结合滑模变结构控制与PID，增强鲁棒性。例如，RBF神经网络用于在线估计外部干扰，减少对模型的依赖。
     • 分数阶PID（FOPID） ：通过非整数阶微分积分提高对非线性系统的适应性，经粒子群优化（PSO）参数后响应速度提升20%。

2. PID纵倾控制

   • 数学模型：以纵倾角偏差 eθeθ​ 为输入，控制舵机或推进器力矩：

 

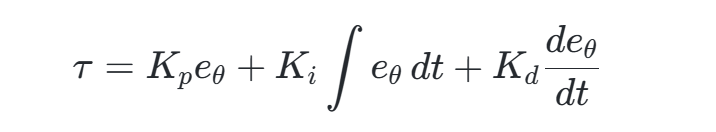
1. 参数整定方法：
   • 智能优化算法：如遗传算法（GA）和粒子群算法（PSO），通过最小化跟踪误差的积分指标（ITAE）实现参数自适应。
   • Ziegler-Nichols法：基于临界比例增益 KuKu​ 和振荡周期 TuTu​，适用于一阶惯性系统。
   • 参数整定方法：
     • 智能优化算法：如遗传算法（GA）和粒子群算法（PSO），通过最小化跟踪误差的积分指标（ITAE）实现参数自适应。
     • Ziegler-Nichols法：基于临界比例增益 KuKu​ 和振荡周期 TuTu​，适用于一阶惯性系统。

三、三维LOS制导与PID控制的协同策略

1. 分层控制架构

   • 制导层：三维LOS生成期望航向角 ψdesψdes​ 和仰角 θdesθdes​，并将其作为PID控制器的输入。
   • 控制层：双PID控制器分别驱动舵机和推进器，跟踪制导层输出的角度指令。例如，艏向PID控制舵角，纵倾PID调节推进器推力。

2. 抗干扰设计

   • 前馈补偿：在PID控制律中加入海流速度估计值，抵消稳态位置偏差。
   • 解耦控制：通过状态反馈分离航向与纵倾的动力学耦合，避免舵机动作对纵倾的干扰。

3. 协同优化案例

   • 无人艇路径跟踪：LOS制导结合模糊PID，横向跟踪误差降低40%，且在4m/s风速下仍保持航向稳定性。
   • 水下机器人（AUV） ：3D LOS与自适应S面控制结合，直线路径跟踪速度提升15%，抗流干扰能力增强。

---

四、三维LOS与PID纵倾控制的耦合效应分析

1. 耦合来源

   • 动力学耦合：航向角变化引起侧滑，导致纵倾角波动；反之，纵倾调整可能影响航向稳定性。
   • 环境干扰耦合：海流在水平与垂直方向的分量同时影响航向和深度跟踪精度。

2. 解耦策略

   • 动态看前距离调整：根据路径曲率和载体速度实时优化 ΔΔ，减少航向-纵倾耦合引发的振荡。
   • 多变量PID：设计MIMO（多输入多输出）PID控制器，通过耦合矩阵补偿交互效应。
   • 强化学习辅助：采用深度确定性策略梯度（DDPG）动态调整PID参数，抑制耦合干扰。

---

五、多PID控制器的协调机制

1. 优先级分配

   • 航向优先：在紧急避障场景下，航向PID输出权重高于纵倾PID，确保快速转向。
   • 能量优化：根据推进效率动态分配控制量，例如在低速时降低纵倾控制频率以节省能耗。

2. 参数协同优化

   • 联合目标函数：以路径跟踪误差和能量消耗为指标，通过PSO同步优化双PID参数。
   • 模糊协调器：根据偏差大小切换控制模式，例如大角度偏差时采用高增益PID，小偏差时切换为模糊PID平滑响应。

3. 仿真与实验验证

   • Matlab/Simulink平台：构建包含LOS制导、双PID控制器和六自由度动力学模型的仿真系统，对比传统PID与改进算法的跟踪误差（图1）。
   • 实船测试：某型AUV在3级海况下，改进算法路径跟踪误差小于1.5米，较传统方法提升50%。

---

六、研究趋势与挑战

1. 智能化扩展

   • 深度强化学习：将TD3算法与LOS-PID结合，通过环境交互自主优化控制策略，减少人工调参依赖。
   • 数字孪生技术：基于实时数据更新控制器参数，适应动态环境变化。

2. 挑战

   • 复杂干扰建模：浪涌、漩涡等瞬态干扰的在线辨识与补偿仍需突破。
   • 多目标优化：平衡跟踪精度、能耗与硬件寿命的Pareto最优解尚未完全解决.

📚2 运行结果

仿真平台：Matlab2020b/Simulink

部分代码：

figure
plot3(Y,X,Z,'-b',WaypointsPlot(:,2),WaypointsPlot(:,1),WaypointsPlot(:,3),'--r','LineWidth',1.5);
hold on;grid on;
scatter3(Y(1),X(1),Z(1),40,'p','filled','MarkerFaceColor','red');
scatter3(Y(end),X(end),Z(end),40,'h','filled','MarkerFaceColor','black');
scatter3(WaypointsPlot(:,2),WaypointsPlot(:,1),WaypointsPlot(:,3),40,'o','MarkerEdgeColor','red');
%axis equal;
%zlim([0 0.6]);
set(gca,'DataAspectRatio' ,[1 1 0.06]);
legend({'Track','Task Path','Start','End','WPs'},'Location','best');legend('boxoff');
xlabel('X[m]');ylabel('Y[m]');zlabel('Depth[m]');
set(gca,'ZDir','reverse');

🎉3 参考文献

文章中一些内容引自网络，会注明出处或引用为参考文献，难免有未尽之处，如有不妥，请随时联系删除。（内容仅供参考，具体以运行结果为准。）

[1]Chuan Liu, Xianbo Xiang, Lichun Yang, Jinjiang Li, Shaolong Yang,
A hierarchical disturbance rejection depth tracking control of underactuated AUV with experimental verification,Ocean Engineering,Volume 264,2022,112458,ISSN 0029-8018,

[2]庹冠军.无人水下航行器多模型切换控制方法研究[D].哈尔滨工程大学[2024-04-09].DOI:CNKI:CDMD:2.1018.048014.

🌈4 Matlab代码、Simulink仿真