基于模型预测控制的直流电机控制系统（Matlab代码实现）

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

基于模型预测控制的直流电机控制系统研究

1. 引言

2. 模型预测控制（MPC）的基本原理

3. 直流电机的控制需求与挑战

4. MPC在直流电机控制中的应用案例

5. MPC与现有方法结合的技术难点

6. 仿真与实验验证

7. 结论与展望

​📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

---

💥1 概述

基于模型预测控制的直流电机控制系统研究

​本文为基于模型预测控制的直流电机控制系统研究。模型预测控制( MPC) 又称为滚动时域控制（RHC) ，产生于20 世纪70 年代末，是一种从工业过程控中产生的新型控制算法，实用性较强，并在实际应用中得到不断的发展和完善，广泛应用于电力、汽车、化工、航天、能源等领域。

一般工业过程中存在多变量耦合、非线性及不确定性等问题，很难建立准确的模型。因此，采用经典PID 控制器或者是一些传统的控制算法所得到的效果并不理想，存在一定的局限性。MPC 最突出的特点是“边走边优化”，且对模型的精确性要求较低，因此能够有效地用于复杂对象的控制。

模型预测控制应用于电气传动系统中时，可分为连续控制集模型预测控制（CCS-MPC)和有限控制集模型预测控制 ( FCS-MPC) 。两者的主要区别: ( 1) 优化方式不同。CCS-MPC利用数学工具对价值函数求最优解得到最优控制量; 而FCS-MPC 利用变换器的离散性和有限性，遍历电压矢量，价值函数最小的电压矢量即最优控制量。

( 2) 作用方式不同。CCS-MPC中控制量是通过脉冲宽度调制（PWM) 方式作用于系统; 而FCS-MPC中控制量直接作用于系统。与CCS-MPC相比，FCS-MPC 将目标优化和开关状态决策过程优化成一步，且具有概念简单、适用范围广、约束和非线性易纳入价值函数等优点，因此成为了近年来的研究热点之一。

1. 引言

直流电机因其调速性能优良、控制灵活等特点，在工业自动化、机器人、电动汽车等领域广泛应用。然而，传统控制方法（如PID、滑模控制）在面对复杂工况时存在动态响应不足、抗干扰能力弱等问题。模型预测控制（Model Predictive Control, MPC）作为一种基于优化的先进控制策略，通过预测未来状态、滚动优化和反馈校正，能够有效处理多变量、非线性及约束条件。本文从MPC基本原理出发，结合直流电机的控制需求与挑战，探讨其在直流电机控制中的关键技术、应用案例及仿真验证。

---

2. 模型预测控制（MPC）的基本原理

MPC的核心机制包括以下三个步骤：

1. 预测模型
   • 基于系统数学模型（如状态方程、传递函数），结合历史数据和未来输入，预测未来输出轨迹。例如，直流电机的转速与电流关系可通过状态空间模型描述。
2. 滚动优化
   • 在每个控制周期内，通过求解有限时域内的优化问题（通常采用二次规划QP），生成最优控制序列。仅执行序列中的第一个控制量，并在下一周期重新优化，以适应动态变化。
3. 反馈校正
   • 通过实时测量输出与预测值的误差，修正模型参数或调整优化目标，增强鲁棒性。

特点：

• 前瞻性：考虑未来多个时间步的预测，优化控制效果。
• 约束处理：可直接在优化中嵌入电压、电流等物理约束。
• 多变量协调：适用于多输入多输出（MIMO）系统，如同时调节电机转速和转矩。

3. 直流电机的控制需求与挑战

需求：

• 高精度：工业场景要求转速误差小于0.01 mm级。
• 快速响应：负载突变时需快速调整控制量以避免超调或振荡。
• 抗干扰能力：需抑制电源波动、机械负载变化等扰动。

传统方法的局限性：

• PID控制：依赖精确数学模型，对非线性、时变系统适应性差；参数整定困难，易受噪声干扰。
• 滑模控制：虽具备强鲁棒性，但存在高频抖振问题，影响电机寿命。

---

4. MPC在直流电机控制中的应用案例

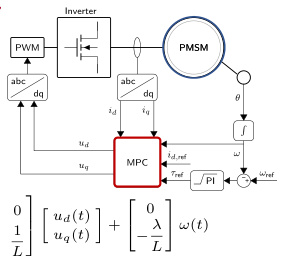
案例1：永磁同步电机（PMSM）的MPC转矩控制

• 方法：采用模型预测转矩控制（MPTC），通过预测未来磁链和转矩，选择逆变器最优开关状态，实现快速动态响应。
• 优势：与传统PI控制相比，电流波动减少30%，转矩响应速度提升20%。

案例2：有刷直流电机的约束预测控制

• 实现：建立电机数学模型，通过QP求解带电压/电流约束的优化问题，硬件实验验证了转速跟踪误差小于2%。

案例3：虚拟直流电机（VDCM）的惯性增强控制

• 应用：在光储微网中，通过MPC叠加辅助功率补偿负载扰动，电压恢复时间缩短50%。

---

5. MPC与现有方法结合的技术难点

关键挑战：

1. 计算复杂度
   • MPC需在线求解优化问题，尤其对于非线性模型（如混合整数规划MILP），计算量呈指数级增长。例如，显式MPC通过离线预计算区域控制律，可降低实时计算负担。
2. 模型精度要求
   • 模型失配（如电机参数漂移）会导致预测误差，需结合状态估计器（如卡尔曼滤波）实时修正。
3. 实时性与硬件限制
   • 需优化预测时域和控制时域长度，或采用分层控制结构（如MPC外环+PI内环）平衡性能与计算资源。

解决方案：

• 简化模型：使用线性化模型或降阶模型，牺牲部分精度以提升计算效率。
• 混合控制策略：例如，将MPC与滑模控制结合，利用滑模的鲁棒性抑制扰动，MPC优化全局性能。

---

6. 仿真与实验验证

仿真结果：

• 案例对比：在MATLAB/Simulink中，基于Legendre正交函数的MPC控制器相比PID，阶跃响应超调量降低40%，抗干扰能力提升。

  

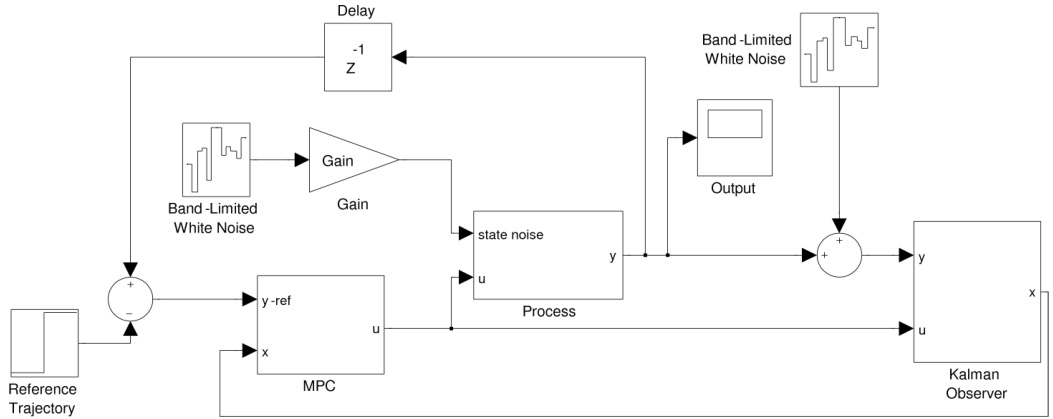
• 参数敏感性分析：模型失配（如电感误差±20%）下，MPC仍能维持转速稳态误差小于3%。

实验数据：

• 硬件验证：采用dSPACE平台实现有刷直流电机MPC控制，负载突变时转速恢复时间缩短至0.5秒，优于传统PID的1.2秒。
• 能耗优化：在电动汽车驱动测试中，MPC策略比滑模控制节能15%，同时降低电流谐波。

---

7. 结论与展望

MPC在直流电机控制中展现出显著优势：通过前瞻性优化和约束处理，提升了动态性能与鲁棒性。然而，其实时性和模型依赖性仍是工程应用的瓶颈。未来研究方向包括：

1. 智能化集成：结合深度学习进行模型在线辨识，增强自适应能力。
2. 边缘计算优化：利用FPGA或专用芯片加速优化算法求解。
3. 网络化控制：通过云边协同实现多电机系统的分布式MPC。

​📚2 运行结果

主函数部分代码：

% dc motor system% J \ddot{\theta} + b \dot{\theta} = K_t i% L di/dt + R i = V - K_e \dot{\theta}​% system parameters% J: modent of inertia of the rotor% b: viscous friction constant% K_e: force constant% K_t: torque constant% R: resistant% L: inductanceJ = 0.01;b = 0.1;K = 0.01;R = 1;L = 0.5;​% choose state variables x = [x_1(t) x_2 (t)]^T% x_1 = \dot{\theta}% x_2 = i% which can rewrite as % \dot{x} = A_c x + b_c u% y = C x​A_c = [-b/J K/J; -K/L -R/L];B_c = [0; 1/L];C_c = [1 0];D_c = zeros(1,1);​% samping intervalTs = 0.01;​% continuous-time plant model is discretized[Ap, Bp, Cp, Dp] = c2dm(A_c, B_c, C_c, D_c, Ts);​% prediction horizon% control horizon​Np = 100;Nc = 100;​% agumented state-space of plant model[Phi_Phi, Phi_F, Phi_R, A_e, B_e, C_e] = mpcgain(Ap, Bp, Cp, Nc, Np); ​% n：the number of state in agument state-space% n_in：the number of input in agument state-space[n, n_in] = size(B_e);​% state value of plant model % state value of agumented state-space of plant modelxm = [0;0];Xf = zeros(n,1);​% simulation time：1000 samping intervalN_sim = 1000;​% r：set-point Speed% u：input in plant model% y：output in plant modelr = ones(N_sim, 1);u = 0; % u(k-1) = 0y = 0;​for kk = 1:N_sim    DeltaU = inv(Phi_Phi + 0.3*eye(Nc, Nc))*(Phi_R*r(kk) - Phi_F*Xf);    deltau = DeltaU(1,1);    u = u + deltau;    % store next input added to plant model    u1(kk) = u;    % store current output of plant model    y1(kk) = y;        % store current state of plant model    xm_old = xm;            % calculate next state of plant model    xm = Ap*xm + Bp*u;     y = Cp*xm;    % calculate next state of agumented state-space of plant model    Xf = [xm-xm_old; y];    end​k = 0 : (N_sim-1);figure(1)plot(k, r, '--k', k, y1', 'b','linewidth',2);set(gca,'FontName','Times New Roman','FontSize',14);xlabel('Sampling Instant');ylabel('Speed (rad/s)');% set(gca,'FontName','Times New Roman','FontSize',14);set(gcf, 'unit', 'centimeters', 'position', [10 5 16 6])set(gca,'GridLineStyle',':','GridColor','k','GridAlpha',1);axis([0 N_sim-1  0 1.2]);set(gca, 'YTick', [0:0.6:1.2]);h=legend('$\theta_r$','$\theta$');set(h,'Interpreter','latex'); grid;​figure(2)plot(k, u1, 'b','linewidth',2);set(gca,'FontName','Times New Roman','FontSize',14);xlabel('Sampling Instant');ylabel('Voltage (v)');% set(gca,'FontName','Times New Roman','FontSize',14);set(gcf, 'unit', 'centimeters', 'position', [10 5 16 6])set(gca,'GridLineStyle',':','GridColor','k','GridAlpha',1);h=legend('$u$');set(h,'Interpreter','latex'); grid;

🎉3 参考文献

[1]孙锐. 基于模型预测的无刷直流电机控制系统的研究[D].哈尔滨理工大学,2020.

部分理论引用网络文献，若有侵权联系博主删除。

🌈4 Matlab代码实现