基于二进制粒子群优化(BPSO)最佳PMU位置(OPP)配置研究（Matlab代码实现）

最新推荐文章于 2025-05-17 13:35:10 发布

Ps.729

最新推荐文章于 2025-05-17 13:35:10 发布

阅读量571

点赞数 23

文章标签： matlab 前端 javascript

本文链接：https://blog.csdn.net/weixin_67304359/article/details/147992148

版权

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

⛳️赠与读者

💥1 概述

基于二进制粒子群优化（BPSO）的最佳PMU位置（OPP）配置研究

一、二进制粒子群优化（BPSO）的基本原理与改进

二、PMU位置优化（OPP）问题定义与约束

三、基于BPSO的OPP方法研究现状

四、典型应用案例与评估指标

五、挑战与未来方向

六、结论

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码、数据

⛳️赠与读者

👨‍💻做科研，涉及到一个深在的思想系统，需要科研者逻辑缜密，踏实认真，但是不能只是努力，很多时候借力比努力更重要，然后还要有仰望星空的创新点和启发点。当哲学课上老师问你什么是科学，什么是电的时候，不要觉得这些问题搞笑。哲学是科学之母，哲学就是追究终极问题，寻找那些不言自明只有小孩子会问的但是你却回答不出来的问题。建议读者按目录次序逐一浏览，免得骤然跌入幽暗的迷宫找不到来时的路，它不足为你揭示全部问题的答案，但若能让人胸中升起一朵朵疑云，也未尝不会酿成晚霞斑斓的别一番景致，万一它居然给你带来了一场精神世界的苦雨，那就借机洗刷一下原来存放在那儿的“躺平”上的尘埃吧。

或许，雨过云收，神驰的天地更清朗.......🔎🔎🔎

💥1 概述

基于二进制粒子群优化（BPSO）的最佳PMU位置（OPP）配置研究

基于二进制粒子群优化（BPSO）的最佳PMU位置（OPP）配置研究是一项涉及电力系统中相位测量单元（PMU）部署的研究。PMU是一种用于实时监测电力系统状态的设备，可以提供高精度的电力数据，对于电力系统的运行和控制非常重要。在研究中，通过使用BPSO算法，结合电力系统的拓扑结构和负荷分布等信息，寻找最佳的PMU位置配置，以实现电力系统的最佳监测覆盖和控制。

一、二进制粒子群优化（BPSO）的基本原理与改进

BPSO是粒子群优化（PSO）的离散版本，专为二进制空间优化问题设计。其核心原理是通过粒子群在二进制空间中搜索最优解，每个粒子的位置由0或1构成，速度决定位置翻转概率。关键步骤包括速度更新、Sigmoid函数映射概率、随机阈值判断位置更新等。公式表达为：

改进方向：

转换函数优化：采用V型函数替代传统S型函数，增强局部搜索能力。
多样性增强：引入自适应变异策略，动态调整变异概率以避免早熟收敛。
信息融合：利用种群平均信息或全局极值，提升收敛速度与稳定性。

优缺点：

优点：适用于高维组合优化问题，参数少且实现简单。
缺点：易陷入局部最优，参数敏感性高，大规模问题计算复杂度大。

二、PMU位置优化（OPP）问题定义与约束

OPP的目标是以最小PMU数量实现电力系统完全可观测性，同时满足成本、通信和物理约束。

数学模型：
- 目标函数：最小化总成本，即min⁡∑k=1nckyk，其中yk∈{0,1}表示是否在节点k安装PMU。
- 约束条件：

可观测性约束：所有节点需通过PMU直接测量或间接推导（如零注入总线）被覆盖。
通道限制：PMU的电压/电流测量通道数不超过硬件容量。
冗余度要求：例如总线可观测性指数（BOI）和总系统冗余指数（TSORI）。

特殊场景处理：
- 零注入总线（ZIB）：通过逻辑约束调整可观测性规则。
- 通信可靠性：需考虑光纤覆盖和冗余链路。

三、基于BPSO的OPP方法研究现状

经典BPSO在OPP中的应用：
- 编码设计：粒子位置向量表示PMU安装节点的二进制选择。
- 适应度函数：结合PMU数量与可观测性覆盖率，如Fitness=α⋅PMU数量+β⋅未观测节点数Fitness=α⋅PMU数量+β⋅未观测节点数。
- 约束处理：通过惩罚函数或启发式修复策略（如最短开停机时间修补）处理约束。
改进BPSO方法：
- BAPSO（Binary Accelerated PSO） ：结合全局与局部拓扑，减少迭代次数，适用于大规模电网。
- 混合算法：如BPSO与遗传算法（GA）结合，利用GA的交叉变异增强多样性。
- 多目标优化：同时最小化PMU数量、最大化冗余度或状态估计精度。
性能对比：
- 与ILP对比：BPSO在复杂约束下表现更灵活，但ILP在小规模问题中精度更高。
- 与其他启发式算法对比：

遗传算法（GA）：BPSO收敛更快，但GA在全局搜索上更优。
龙飞算法（DA）：DA在多目标优化中表现更稳定。

四、典型应用案例与评估指标

案例研究：
- IEEE测试系统：如IEEE 14/30/118节点系统，验证BPSO在不同规模下的有效性。
- 实际电网：如土耳其400 kV电网，BPSO减少PMU数量约20%。
评估指标：
- 可观测性覆盖率：确保所有节点可观测。
- 经济性：PMU安装成本与通信基础设施费用。
- 算法效率：收敛速度、迭代次数和计算时间。

五、挑战与未来方向

现存问题：
- 大规模电网中计算复杂度高。
- 动态电网拓扑（如可再生能源波动）适应性不足。
改进方向：
- 分布式BPSO：利用并行计算加速大规模问题求解。
- 深度强化学习融合：动态调整算法参数以适应电网变化。
- 多类型PMU协同：结合M型（高精度）与P型（快速响应）PMU的配置优化。

六、结论

BPSO在OPP问题中展现了较强的适应性与灵活性，尤其在处理离散约束和高维优化时具有优势。通过算法改进（如BAPSO、混合策略）和硬件协同设计（如通信冗余），可进一步提升其工程实用性。未来需结合新型优化理论与电力系统动态需求，推动OPP方法向智能化、实时化方向发展。

📚2 运行结果

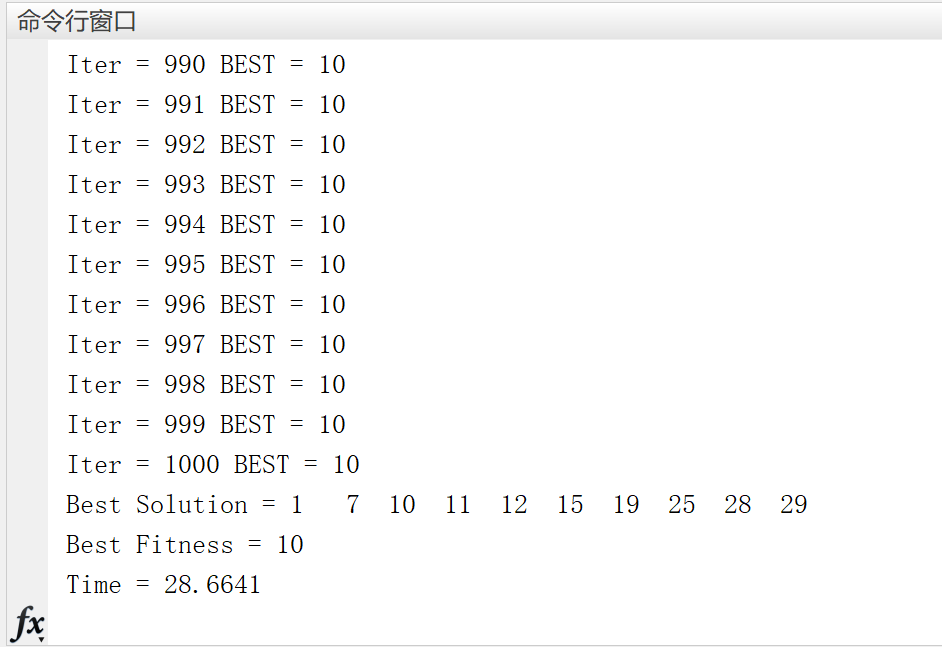
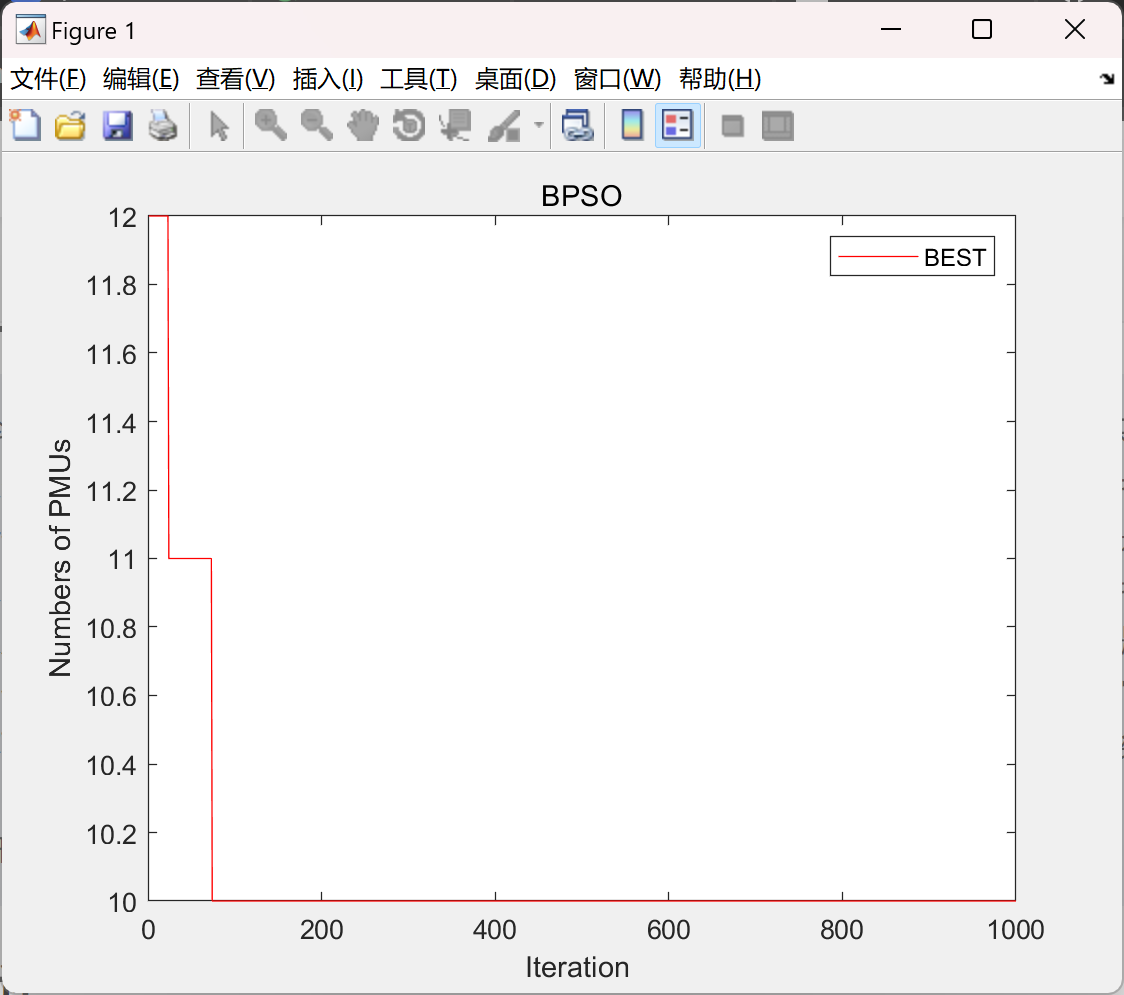
部分代码：

function [Z, SORI]=IEEE_30_Bus(x1)
Z = zeros(size(x1,1),1);
nVar = size(x1,2);

for ii = 1:size(x1,1)
x=x1(ii,:);
end

ldata = [
   1   2   0.0192   0.0575   0.0528   0   0   0   0   0   1   -360   360;
   1   3   0.0452   0.1652   0.0408   0   0   0   0   0   1   -360   360;
   2   4   0.057   0.1737   0.0368   0   0   0   0   0   1   -360   360;
   3   4   0.0132   0.0379   0.0084   0   0   0   0   0   1   -360   360;
   2   5   0.0472   0.1983   0.0418   0   0   0   0   0   1   -360   360;
   2   6   0.0581   0.1763   0.0374   0   0   0   0   0   1   -360   360;
   4   6   0.0119   0.0414   0.009   0   0   0   0   0   1   -360   360;
   5   7   0.046   0.116   0.0204   0   0   0   0   0   1   -360   360;
   6   7   0.0267   0.082   0.017   0   0   0   0   0   1   -360   360;
   6   8   0.012   0.042   0.009   0   0   0   0   0   1   -360   360;
   6   9   0   0.208   0   0   0   0   0.978   0   1   -360   360;
   6   10   0   0.556   0   0   0   0   0.969   0   1   -360   360;
   9   11   0   0.208   0   0   0   0   0   0   1   -360   360;
   9   10   0   0.11   0   0   0   0   0   0   1   -360   360;
   4   12   0   0.256   0   0   0   0   0.932   0   1   -360   360;
   12   13   0   0.14   0   0   0   0   0   0   1   -360   360;
   12   14   0.1231   0.2559   0   0   0   0   0   0   1   -360   360;
   12   15   0.0662   0.1304   0   0   0   0   0   0   1   -360   360;
   12   16   0.0945   0.1987   0   0   0   0   0   0   1   -360   360;
   14   15   0.221   0.1997   0   0   0   0   0   0   1   -360   360;
   16   17   0.0524   0.1923   0   0   0   0   0   0   1   -360   360;
   15   18   0.1073   0.2185   0   0   0   0   0   0   1   -360   360;
   18   19   0.0639   0.1292   0   0   0   0   0   0   1   -360   360;
   19   20   0.034   0.068   0   0   0   0   0   0   1   -360   360;
   10   20   0.0936   0.209   0   0   0   0   0   0   1   -360   360;
   10   17   0.0324   0.0845   0   0   0   0   0   0   1   -360   360;
   10   21   0.0348   0.0749   0   0   0   0   0   0   1   -360   360;
   10   22   0.0727   0.1499   0   0   0   0   0   0   1   -360   360;
   21   22   0.0116   0.0236   0   0   0   0   0   0   1   -360   360;
   15   23   0.1   0.202   0   0   0   0   0   0   1   -360   360;
   22   24   0.115   0.179   0   0   0   0   0   0   1   -360   360;
   23   24   0.132   0.27   0   0   0   0   0   0   1   -360   360;
   24   25   0.1885   0.3292   0   0   0   0   0   0   1   -360   360;
   25   26   0.2544   0.38   0   0   0   0   0   0   1   -360   360;
   25   27   0.1093   0.2087   0   0   0   0   0   0   1   -360   360;
   28   27   0   0.396   0   0   0   0   0.968   0   1   -360   360;
   27   29   0.2198   0.4153   0   0   0   0   0   0   1   -360   360;
   27   30   0.3202   0.6027   0   0   0   0   0   0   1   -360   360;
   29   30   0.2399   0.4533   0   0   0   0   0   0   1   -360   360;
   8   28   0.0636   0.2   0.0428   0   0   0   0   0   1   -360   360;
   6   28   0.0169   0.0599   0.013   0   0   0   0   0   1   -360   360;
];

A=[];
% Create Adjacency Matrix
for c1=1:size(ldata,1)
A(ldata(c1,1),ldata(c1,2))=1;
A(ldata(c1,2),ldata(c1,1))=1;
A(ldata(c1,2),ldata(c1,2))=1;
A(ldata(c1,1),ldata(c1,1))=1;
end

u=ones(nVar,1);
% x=round(x);
f=A*(x');
a=f.*u;
SORI = sum(a);
d=find(a==0);
if isempty(d)
Z=sum(x);
else
Z=numel(d)*nVar;
end
end