【电力系统综合能源】“双碳“背景下|综合能源系统中的经济-二氧化碳排放协调最优调度和敏感性分析研究（Matlab代码实现）

最新推荐文章于 2025-05-16 17:40:27 发布
最新推荐文章于 2025-05-16 17:40:27 发布
阅读量926 收藏 17
点赞数 14
文章标签： 能源 matlab 算法
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/weixin_67304359/article/details/147992328
版权

 👨‍🎓个人主页

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

双碳背景下综合能源系统经济-碳排放协调优化调度与敏感性分析研究

一、研究背景与政策驱动

二、经济-碳排放协调优化模型构建

三、综合能源系统最优调度算法

四、敏感性分析在协调优化中的应用

五、现有研究结合经济-碳排放模型与调度算法的成果

六、挑战与未来方向

七、结论

📚2 运行结果

🎉3 参考文献

 🌈4 Matlab代码、数据下载

💥1 概述

双碳背景下综合能源系统经济-碳排放协调优化调度与敏感性分析研究

综合能源系统（IES）因其在能源效率和可再生能源消费方面的优异表现而在工程应用中具有广阔的前景。在IES中，热舒适度同时受到加热功率，建筑物参数和室外温度的影响。因此，室外温度的不确定性会对热舒适性带来一些不利影响，在IES的调度决策中需要考虑这一点。

“双碳”战略倡导绿色、环保、低碳的生活方式。加快降低碳排放步伐，有利于引导绿色技术创新，提高产业和经济的全球竞争力。中国持续推进产业结构和能源结构调整，大力发展可再生能源，在沙漠、戈壁、荒漠地区加快规划建设大型风电光伏基地项目，努力兼顾经济发展和绿色转型同步进行。碳排放量是指在生产、运输、使用及回收某产品时所产生的温室气体排放量。而动态的碳排放量，则是指每单位货品累积排放的温室气体量。

为了减轻全球变暖的威胁，CO2减排是电力系统可持续发展不可逆转的趋势。在各种低碳技术中，燃气发电厂和电转气设施在减少排放方面发挥着重要作用，它们正在增加电力和天然气系统之间的相互依存关系。同时考虑到风力发电渗透率的提高，本文提出了一种在电力和天然气系统约束下低碳经济调度模型。减少二氧化碳在排放和提高风电利用率方面，提出了燃烧后碳捕集系统和电转气设施的数学公式。此外，进一步分析了燃烧后碳捕集系统和电转气设施的灵活运行模式。所提出的模型的目标功能是最小化总成本，其中包括运营成本，CO2弃风的处理成本和罚金成本。然后将优化模型转换为混合整数线性规划问题，以实现高效的计算目的。通过数值算例验证了所提模型和灵活运行模式的有效性。

一、研究背景与政策驱动

在“双碳”目标（2030年碳达峰、2060年碳中和）的约束下，中国正加速推进能源系统低碳转型。传统能源系统以单一能源形式独立运行的模式已无法满足减排需求，而综合能源系统（Integrated Energy System, IES）通过整合电力、热力、天然气、可再生能源等多能源形式，实现协同优化和互补互济，成为实现能源高效利用与低碳转型的关键载体。政策层面，中国正从“能耗双控”向“碳排放双控”转型，通过碳交易市场、碳定价机制等工具驱动经济-碳排放的协调优化。

二、经济-碳排放协调优化模型构建

  1. 多目标优化框架
    经济-碳排放协调优化的核心在于平衡系统运行成本与碳排放量。典型模型以总成本最小化和碳排放量最小化为双目标函数，结合能源供需平衡、设备运行约束等条件。例如：

    • 动态投入产出模型：以GDP累计最大化和碳排放总量最小化为目标，考虑产业动态投入产出平衡与能源消耗约束。
    • 碳能耦合模型：引入阶梯式碳交易机制，将碳成本纳入目标函数，通过碳价调节企业减排行为。
    • 相对发展系数模型：通过计算经济高质量发展系统与碳排放系统的领先/滞后程度（E=U1/U2E=U1​/U2​），动态调整优化方向。

  2. 关键约束条件

    • 能源流平衡：电、热、气、氢等多能源的输入-转换-输出平衡。

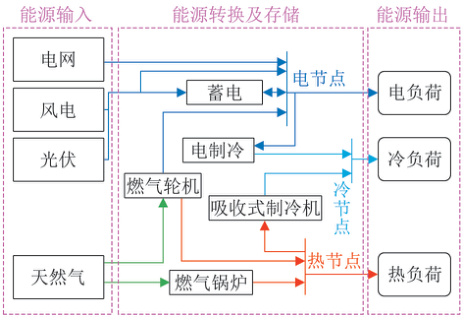
    • 设备运行限制：如燃气轮机爬坡率、储能充放电效率、碳捕集系统能耗等。
    • 政策约束：碳排放配额、可再生能源消纳率、碳交易价格波动等。

  3. 技术创新融合

    • 碳捕集与电转气（P2G）协同：通过碳捕集系统回收CO₂，结合P2G技术生成甲烷，实现碳循环利用。
    • 氢能耦合：利用电解水制氢技术消纳可再生能源，降低系统碳排放。
三、综合能源系统最优调度算法

  1. 传统优化算法

    • 混合整数线性规划（MILP） ：适用于确定性场景下的多目标优化，计算效率高但依赖精确模型。
    • 遗传算法与粒子群优化：在多约束非凸问题中表现良好，但易陷入局部最优。

  2. 智能算法创新

    • 分布式可信鲁棒优化：基于双步投影算法，将随机变量转化为确定性模型，提升多区域互联系统的鲁棒性。
    • 深度强化学习（DRL） ：利用TD3算法优化碳捕集与P2G设备的协同运行，实时响应需求波动与能源价格变化。
    • 生成对抗模仿学习（GAIL） ：结合生成对抗网络与模仿学习，提升复杂能源流调度的自适应能力。

  3. 多时间尺度调度
    分层优化框架（日前-日内-实时）通过混沌万有引力算法与YALMIP工具箱结合，降低运行成本误差约15%。

四、敏感性分析在协调优化中的应用
  1. 全局敏感性分析方法
    • Sobol方差分解法：量化参数对系统性能的单独影响与交互作用，适用于多阶段敏感性分析（如设备老化、环境变化）。
    • Morris抽样与蒙特卡洛模拟：识别关键不确定参数（如能源价格、碳价、可再生能源出力），优化系统规划决策。


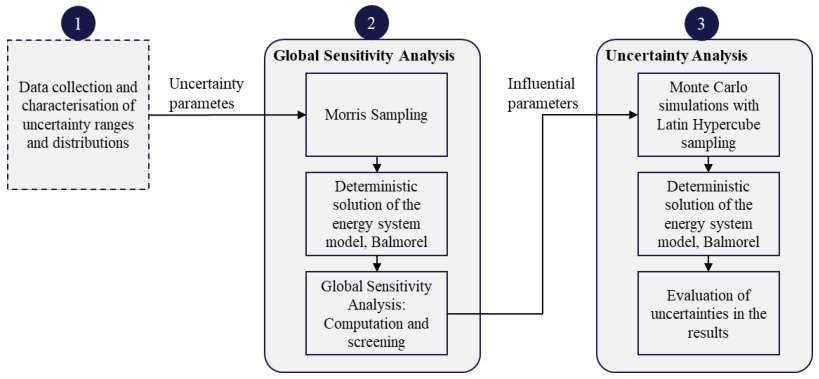
2. 敏感性指标设计

  • 经济-碳协调敏感性：包括全球/本地碳减排成本、政策强度对调度结果的影响。
  • 参数敏感性分级：例如，在分布式能源系统中，燃气轮机效率与光伏容量对总成本的影响显著高于储能寿命。
  1. 案例分析
    • 碳价敏感性：碳价每增加10元/吨，系统总成本上升3.8%，但碳排放量下降12.5%。
    • 可再生能源渗透率：风电渗透率提高至30%时，需配套P2G设备以避免弃风，系统经济性提升8.2%。
五、现有研究结合经济-碳排放模型与调度算法的成果

  1. 低碳经济调度模型

    • Matlab实现案例：构建包含光伏、风电、碳捕集设备的IES模型，通过MILP求解，验证总成本降低18.6%、碳排放减少24.3%。
    • 季节性优化调度：考虑“电热气碳”耦合与需求响应，冬季供热期碳排放量较夏季高35%，需动态调整碳交易配额。

  2. 算法性能对比

    • TD3算法 vs 传统优化：在含储能场景下，TD3算法使运行成本降低12.7%，收敛速度提升40%。
    • AMOWOA算法：通过模糊一致矩阵选取全局最优解，在华东某商业园区案例中节省运行成本5.8%。

  3. 政策工具协同效应

    • 阶梯式碳交易与需求响应：碳交易成本降低36.25%，天然气负荷碳排放因子优化后系统总排放减少18.52%。
    • 绿色金融支持：碳债券与绿色信贷为IES低碳改造提供资金，降低项目融资成本约2.5%。
六、挑战与未来方向

  1. 技术挑战

    • 多能流耦合复杂性：电-热-气-氢耦合方程的强非线性导致求解困难，需开发高效降维算法。
    • 不确定性建模：可再生能源出力与负荷波动的概率分布难以精确刻画，需结合GAN等生成模型增强预测精度。

  2. 政策与市场机制

    • 碳价动态调控：需建立碳价与能源价格的联动机制，避免市场投机。
    • 跨区域协调：打破省际碳交易壁垒，构建全国统一碳市场。

  3. 研究方向

    • 数字孪生技术：通过虚拟仿真优化调度策略，减少物理实验成本。
    • 社区级IES微网：结合用户侧共享储能与分布式光伏，提升区域能源自给率。
七、结论

在双碳目标驱动下，综合能源系统的经济-碳排放协调优化已成为能源转型的核心议题。通过多目标优化模型与智能算法的结合，结合阶梯式碳交易、氢能耦合等技术创新，能够实现运行成本与碳排放的协同降低。敏感性分析则为政策制定与系统设计提供关键参数影响评估。未来需进一步突破多能流耦合建模、不确定性处理等技术瓶颈，并完善碳市场与绿色金融支持体系，推动IES向高效、低碳、韧性方向持续发展。

📚2 运行结果

部分代码：

function define_objective()
global data model
price_buy=data.mpc.cost(1,:);
price_sell=0.49;%0.49

model.cost.Cgrid_buy=sum((10000*model.judge.Pbuy).*price_buy);
model.cost.Cgrid=model.cost.Cgrid_buy;
%% calculate CO2
%购电部分产生的CO2
model.CO2_buy_grid=0.5810*sum(sum(10000*model.judge.Pbuy));%
%data.E_G表示六台发电机组的机组节点碳势，碳排放等于节点碳势乘以出力乘以时间
P_g=[10000*model.p_wt(1,:); 10000*model.judge.P_CHP; 10000*model.p_wt(2,:); 10000*model.p_wt(3,:); 10000*model.p_wt(4,:)];
%5*24,10是chp，其他的都是风力发电机和蓄电池
p_H=[model.judge.H_CHP;model.judge.H_GB];%1*24,6/51节点热网管道都只有一个热源点
data.E_G=([0; 443; 0; 0; 0]/1000)';
data.E_H=([443.0;516]/1000)';
model.CO2_all=0;
CO2_G=sum(sum(data.E_G*P_g));
CO2_H=sum(sum(data.E_H*p_H));
model.CO2_all=CO2_G + CO2_H +model.CO2_buy_grid;
model.CO2_e=CO2_G +model.CO2_buy_grid;
%%%%%%%%%%%
model.CO2_chp=CO2_G;
model.CO2_grid=model.CO2_buy_grid;
model.CO2_GB=sum(sum(model.judge.H_GB*0.516));
model.CO2_CHP_all=sum(sum(model.judge.H_CHP*0.443+10000*model.judge.P_CHP*0.443));

%% calculat cost
model.cost.CHP.coal = 0;%CHP机组煤耗成本
c_gas=0.575;%0.571
model.cost.CHP.coal=c_gas*(sum(model.judge.P_CHP*10000)/0.3+sum(model.judge.H_GB)/0.99);
model.cost.CHP.total = model.cost.CHP.coal ;%CHP机组总成本
%% IES运行成本
model.cost.IES_run = 0;%运行成本
K_ESS=0.01685;%运行维护费用
K_CHP=0.0480;%CHP机组运行维护
K_WT=0.02;%风机运行维护费用
K_TST=0.013;
K_GB=0.0457;
model.cost.IES_run = ...
    (K_WT*(sum(sum(model.p_wt*10000))) +...
    K_CHP*(sum(sum(model.judge.P_CHP*10000))) + K_CHP*(sum(sum(model.judge.H_CHP)))+...
    K_ESS*(sum(sum(abs(model.judge.P_BT_charge*10000)))+sum(sum(abs(model.judge.P_BT_discharge*10000))))+...
    K_TST*(sum(sum(abs(model.judge.H_HS_in)))+sum(sum(abs(model.judge.H_HS_out)))) +...
    +K_GB*(sum(sum(model.judge.H_GB))));

model.cost_obj=model.cost.IES_run+model.cost.CHP.total+model.cost.Cgrid;
model.CO2_obj=model.CO2_all;
model.obj1=model.cost_obj;
model.obj2=model.CO2_obj;

%% 探究CHP局部碳减排对整体的影响
% %CHP
% m1=20;
% F2_new=zeros(20,1);
% F1_new=zeros(20,1);
% delta_F2=zeros(20,1);delta_F1=zeros(20,1);
% delta_CHP=zeros(20,1);
% TCHP=[66160.1645700000;68976.7318400000;71645.5313900000;74103.2038300000;76521.0783900000;78679.2305400000;80742.9631200000;82804.0476000000;84911.6212500000;86869.0288500000;88655.3394400000;90413.9354200000;92105.2402400000;93780.6945400000;95433.8139400000;97083.8130600000;98890.4039000000;100980.876600000;102750.906500000;104150.187000000];
% F1=[182397.865916657;182524.454718706;182675.316393106;182843.134267172;183027.782553574;183228.697592839;183438.388926405;183656.462514397;183880.874738848;184110.915454502;184345.403398763;184584.078607678;184827.138496165;185074.596797007;185326.364934565;185582.768660740;185844.357913700;186129.989065402;186480.836239024;186930.763229854];
% F2=[141803.691569005;141317.147058091;140864.257716798;140434.915506760;140028.866895398;139645.413181390;139274.106101138;138914.439585869;138563.569474724;138220.510988072;137883.603197424;137552.507168951;137227.498830555;136908.614797601;136595.665226767;136289.151004832;135989.846523783;135723.884964778;135548.397844598;135513.839067998];
% %循环求CHP的CLCER
% for j=1:m1
%     model.st_New_CHP1= [model.st, model.CO2_CHP_all ==TCHP(j,1)-200];%CHP源节点10的碳排放约束
%     model.st_New_CHP1= [model.st_New_CHP1, model.obj2== F2(j,1)];
%     model.ops=sdpsettings('verbose', 0, 'solver', 'cplex');
%     model.sol=optimize(model.st_New_CHP1,model.obj1,model.ops);
%     F1_new(j,1)=value(model.obj1);
%     delta_F1(j,1)=F1_new(j,1)-F1(j,1);
%     delta_CHP(j,1)=200;
%     if model.sol.problem == 0
%         disp('succcessful solved');disp(j);
%     else
%         disp('error');disp(j);
%         yalmiperror(model.sol.problem)
%     end
% end
% CLCER_CHP=delta_F1./delta_CHP;
% %循环求CHP的SLCER
% for j=1:m1
%     model.st_New_CHP2= [model.st, model.CO2_CHP_all ==TCHP(j,1)-200];%CHP源节点10的碳排放约束
%     model.st_New_CHP2= [model.st_New_CHP2, model.obj1== F1(j,1)];
%     model.ops=sdpsettings('verbose', 0, 'solver', 'cplex');
%     model.sol=optimize(model.st_New_CHP2,model.obj2,model.ops);
%     F2_new(j,1)=value(model.obj2);
%     delta_F2(j,1)=F2_new(j,1)-F2(j,1);
%     delta_CHP(j,1)=200;
%     if model.sol.problem == 0
%         disp('succcessful solved');disp(j);
%     else
%         disp('error');disp(j);
%         yalmiperror(model.sol.problem)
%     end
% end
% SCER_CHP=delta_F2./delta_CHP;
%% 探究GB局部碳减排对整体的影响
% %GB
% m1=20;
% F2_new=zeros(20,1);F1_new=zeros(20,1);
% delta_F2=zeros(20,1);delta_F1=zeros(20,1);
% delta_GB=zeros(20,1);
% TGB=[61699.5287800000;59410.2323600000;57243.6428100000;55248.3810600000;53294.7231400000;51542.0055800000;49862.4904900000;48185.0340100000;46474.2228200000;44885.6794100000;43435.5165300000;42008.6072800000;40636.0495000000;39276.5557900000;37934.4916300000;36594.9716600000;35127.6683500000;33428.4465200000;32050.6095000000;31094.1468600000];
% F1=[182397.865916657;182524.454718706;182675.316393106;182843.134267172;183027.782553574;183228.697592839;183438.388926405;183656.462514397;183880.874738848;184110.915454502;184345.403398763;184584.078607678;184827.138496165;185074.596797007;185326.364934565;185582.768660740;185844.357913700;186129.989065402;186480.836239024;186930.763229854];
% F2=[141803.691569005;141317.147058091;140864.257716798;140434.915506760;140028.866895398;139645.413181390;139274.106101138;138914.439585869;138563.569474724;138220.510988072;137883.603197424;137552.507168951;137227.498830555;136908.614797601;136595.665226767;136289.151004832;135989.846523783;135723.884964778;135548.397844598;135513.839067998];
% %循环求GB的CLCER
% for j=1:m1
%     model.st_New_GB1= [model.st, model.CO2_GB ==TGB(j,1)-100];%CHP源节点10的碳排放约束
%     model.st_New_GB1= [model.st_New_GB1, model.obj2== F2(j,1)];
%     model.ops=sdpsettings('verbose', 0, 'solver', 'cplex');
%     model.sol=optimize(model.st_New_GB1,model.obj1,model.ops);
%     F1_new(j,1)=value(model.obj1);
%     delta_F1(j,1)=F1_new(j,1)-F1(j,1);
%     delta_GB(j,1)=100;
%     if model.sol.problem == 0
%         disp('succcessful solved');disp(j);
%     else
%         disp('error');disp(j);
%         yalmiperror(model.sol.problem)
%     end
% end
% CLCER_GB=delta_F1./delta_GB;
% %循环求GB的SLCER
% for j=1:m1
%     model.st_New_GB2= [model.st, model.CO2_GB ==TGB(j,1)-100];%CHP源节点10的碳排放约束
%     model.st_New_GB2= [model.st_New_GB2, model.obj1== F1(j,1)];
%     model.ops=sdpsettings('verbose', 0, 'solver', 'cplex');
%     model.sol=optimize(model.st_New_GB2,model.obj2,model.ops);
%     F2_new(j,1)=value(model.obj2);
%     delta_F2(j,1)=F2_new(j,1)-F2(j,1);
%     delta_GB(j,1)=100;
%     if model.sol.problem == 0
%         disp('succcessful solved');disp(j);
%     else
%         disp('error');disp(j);
%         yalmiperror(model.sol.problem)
%     end
% end
% SCERP_GB=delta_F2./delta_GB;

%% 准备求Pareto
model.ops=sdpsettings('verbose', 0, 'solver', 'cplex');
model.sol=optimize(model.st,model.obj1,model.ops);
if model.sol.problem == 0
    disp('succcessful solved');
else
    disp('error');
    yalmiperror(model.sol.problem)
end
data.G1_x1=value(model.obj1);
data.G2_x1=value(model.obj2);
model.ops=sdpsettings('verbose', 0, 'solver', 'cplex');
model.sol=optimize(model.st,model.obj2,model.ops);
data.G1_x2=value(model.obj1);
data.G2_x2=value(model.obj2);
if model.sol.problem == 0
    disp('succcessful solved');
else
    disp('error');
    yalmiperror(model.sol.problem)
end

🎉3 参考文献

部分理论来源于网络，如有侵权请联系删除。

[1]S. Lu, W. Gu, S. Zhou, S. Yao and G. Pan, "Adaptive Robust Dispatch of Integrated Energy System Considering Uncertainties of Electricity and Outdoor Temperature," in IEEE Transactions on Industrial Informatics, vol. 16, no. 7, pp. 4691-4702, July 2020, doi: 10.1109/TII.2019.2957026.

[2]陆帅,陈帅,余威,方俊,丁海龙.惯性辅助GNSS跟踪环路技术研究[J].航天控制,2016,34(01):20-24.DOI:10.16804/j.cnki.issn1006-3242.2016.01.004.

[3]姚帅,顾伟,张雪松,赵波,陆帅,吴晨雨.热网特性对于综合能源系统超短期调度的影响[J].电力系统自动化,2018,42(14):83-90.

 🌈4 Matlab代码、数据下载

Ps.729
关注
综合能源系统中的经济-碳协调：最优调度和灵敏度分析【IEEE33节点】（Matlab代码实现）
q216605q的博客
02-16 832
综合能源系统（IES）因其在能源效率和可再生能源消费方面的优异表现而在工程应用中具有广阔的前景。然而，在IES中，热舒适度同时受到加热功率、建筑物参数和室外温度的影响，室外温度的不确定性会对热舒适性带来不利影响，因此需要在IES的调度决策中加以考虑。同时，随着“双碳”战略的提出，加快降低碳排放步伐，引导绿色技术创新，提高产业和经济的全球竞争力已成为重要任务。在此背景下，对综合能源系统中的经济-二氧化碳排放协调最优调度和灵敏度进行分析研究具有重要意义。
【电力系统】基于改进粒子群算法的含碳捕集微网多时间尺度低碳经济调度Matlab代码.rar
10-07
在电力系统领域，如何有效地结合碳捕集技术进行低碳经济调度，实现能源的高效利用和碳排放的最小化，是当前研究的热点之一。粒子群算法作为一种优化算法，在解决此类问题上展现出独特的优势。基于改进粒子群算法的含...
【电力系统综合能源】“双碳“背景下综合能源系统中的经济-二氧化碳排放协调最优调度和敏感性分析研究附Matlab代码
Matlab_jiqi的博客
02-25 734
在全球气候变化日益严峻的背景下，实现“碳达峰、碳中和”目标已成为中国经济社会可持续发展的核心战略。电力系统作为能源供应的关键环节，在实现“双碳”目标中扮演着举足轻重的角色。然而，传统电力系统往往以追求经济效益为主要目标，忽略了碳排放带来的环境影响。因此，综合能源系统（Integrated Energy System, IES）应运而生，它通过整合多种能源形式（电力、热力、天然气等），实现能源的梯级利用和优化配置，为电力系统的低碳转型提供了新的思路和可行性方案。
【电力系统综合能源】“双碳“背景下综合能源系统中的经济-二氧化碳排放协调最优调度和敏感性分析研究 附Matlab代码.rar
02-23
本研究聚焦于“双碳”背景下电力系统综合能源系统的经济-二氧化碳排放协调最优调度问题，通过Matlab编程语言实现了模型的构建、仿真和敏感性分析。研究成果不仅对学术界有重要的贡献，也为实践提供了可操作的策略和...
【电力系统综合能源】“双碳“背景下综合能源系统中的经济-二氧化碳排放协调最优调度和敏感性分析研究附Matlab代码.rar
05-11
1.版本：matlab2014/2019a/2024a 2.附赠案例数据可直接运行。 3.代码特点：参数化编程、参数可方便更改、代码编程思路...4.适用对象：计算机，电子信息工程、数学等专业的大学生课程设计、期末大作业和毕业设计。
PSD-PF对电力系统经济性分析的贡献：深入解析与案例分析
![PSD-PF对电力系统经济性分析的贡献：深入...本文深入探讨了PSD-PF在电力系统中的作用，阐述了电力系统经济性分析的基础理论及其指标。文章详细分析了PSD-PF在负荷预测、调度优化、系统扩展性评估与规划中的应用，以
特斯拉虚拟电厂：能源互联网时代的分布式革命
beige888的博客
05-16 575
特斯拉虚拟电厂的实践表明，数字孪生技术正在重塑能源系统的运行逻辑与价值创造模式。随着IEEE 2030.2标准的推进，虚拟电厂将与交通网、天然气网深度耦合，构建起多能互补的智慧能源生态系统。在双碳目标与能源转型的双重驱动下，特斯拉虚拟电厂（Virtual Power Plant, VPP）通过数字孪生技术与能源系统的深度融合，重构了传统电力系统的运行范式。特斯拉虚拟电厂采用"云-边-端"三层架构，构建起覆盖能源生产、存储、消费的全链路数字孪生体，实现物理世界与信息世界的实时映射与闭环控制。
安科瑞AcrelEMS3.0企业微电网智慧能源平台-安科瑞 蒋静
Acreljing的博客
05-16 255
安科瑞微电网系统解决方案，通过在企业内部的源、网、荷、储、充的各个关键节点安装安科瑞自主研发的各类监测、分析、保护、治理装置；通过控制、计量、通信等技术，将分布式电源、储能系统、可控负荷、电动汽车、电能路由器聚合在一起；平台根据电网价格、用电负荷、电网调度指令等情况，灵活调整微电网控制策略并下发给储能、充电桩、逆变器等系统与设备，保证企业微电网始终安全、可靠、节约、高效、经济、低碳的运行。解决方案-分布式光伏监控系统。解决方案-工商业储能系统。解决方案-有序充电系统。解决方案-光储充系统。
砷化镓太阳能电池：开启多元领域能源新篇
qyresearch_的博客
05-14 616
三结和四结砷化镓太阳能电池则进一步增加了结的数量，能够更充分地吸收不同波长的太阳光，从而实现更高的转换效率，但成本也相对较高，主要应用于对能源需求较大、对成本相对不敏感的航天和军事领域。对于砷化镓太阳能电池企业而言，应加大研发投入，不断提升电池的转换效率和稳定性，降低成本，以增强市场竞争力。在民用领域，随着技术的不断进步和成本的降低，砷化镓太阳能电池也开始逐渐崭露头角。砷化镓太阳能电池可根据连接方式分为单结砷化镓太阳能电池、双结砷化镓太阳能电池、三结砷化镓太阳能电池和四结砷化镓太阳能电池。
能源数字化转型关键引擎：Profinet转Modbus TCP网关驱动设备协同升级
最新发布
gongkong666的博客
05-16 264
无论你的设备是基于ModbusTCP协议的回收设备，还是基于Profinet协议的煤化工设备，只需要通过这个网关，就能实现设备的完美对接。首先，它的安装和使用都非常简单。例如，在回收行业中，通过使用我们的网关，可以轻松地将各种基于ModbusTCP协议的回收设备与基于Profinet协议的管理系统进行连接，实现了设备数据的实时监控和远程控制。Profinet转Modbus TCP网关不仅能够解决设备间的通信问题，还能够提高设备的工作效率和安全性，是回收及煤化工行业中不可或缺的一款产品。
AI智能分析网关V4助力工厂/工地/车间/能源矿山场景玩手机行为精准检测与安全生产智能化监管
EasyDSS官方技术博客
05-13 515
在数字化时代，智能手机的广泛使用给特定场景带来诸多管理挑战。在工业生产、教育教学、危化品作业等场所，人员玩手机易引发安全隐患。
多通道电源管理芯片在分布式能源系统中的优化策略
ANSILIC的博客
05-16 722
在分布式能源系统轻载运维阶段，例如储能系统待机、传感器网络低频采样时段，启用DCM模式可显著降低开关损耗与电磁干扰，此时电感电流断续模式运作，输出纹波控制于适中水平，芯片转换效率较FCCM模式提升超15%。在电气特性方面，其具备4V至14V的宽域输入电压容忍度，能从容适配多种能源前端输出及供电场景，输出电压的宽幅调节范围配合高精度控制，可精准匹配多种负载需求，实现电能的按需精准配送。输出跟踪模式下，储能系统充放电转换时，各通道按预设时序、斜率调整输出，避免电池过充、过放。
交通运输与能源融合发展——光储充在交通上的应用完整解决方案
AcrelGHP的博客
05-15 1010
在公路领域，利用高速公路沿线服务区等建设清洁能源项目，推广新技术，建设充（换）电站等。一方面，加强开发要素保障，强化用地、用海等资源支持，推动交通与能源基础设施共享资源，优化清洁能源年度开发方案，加强沿线配电网建设。另一方面，创新开发管理模式，在交通基础设施工程项目可行性研究中增加清洁能源开发利用专章，鼓励同步开发、同步招商，统一办理核准（备案）手续，同步办理涉路施工许可。同时，推动交通运输与能源产业补链强链，培育相关产业，保障原材料供应，推动产业升级，拓展市场需求，做强产业集群。
22、能源监控与优化 - 数据中心模拟 - /能源管理组件/data-center-energy-monitoring
地上一の鹅的博客
05-16 768
76个工业组件库示例汇总本组件旨在模拟一个典型数据中心的能源消耗情况，并提供实时的监控数据和基本的优化建议/警报功能。用户可以通过界面直观地了解数据中心总体功耗、PUE (电源使用效率)、各部分能耗构成、机架温度状态等关键指标，并观察其动态变化。
基于matlab的D2D 功率控制仿真
hie98894的博客
05-16 237
基于MATLAB的D2D（Device-to-Device）功率控制仿真示例，包含系统建模、功率控制算法实现和性能分析。该仿真以蜂窝网络为背景，重点关注D2D用户间的干扰管理和功率优化。
matlab多项式
Cao123456789321的博客
05-15 505
多项式用行向量表示，按降幂排列系数。例如，多项式 3x2+2x+1 表示为。通过掌握这些函数和操作，可以在MATLAB中高效处理多项式相关计算。函数用于分解有理分式。
【MATLAB例程】线性卡尔曼滤波的程序，三维状态量和观测量，较为简单，可用于理解多维KF，附代码下载链接
MATLAB卡尔曼的博客
05-16 639
本文介绍了一个三维状态的扩展卡尔曼滤波（EKF）算法的实现。代码通过生成过程噪声和观测噪声，对真实状态进行滤波估计，并对比了滤波前后状态量的误差和误差累积分布曲线。代码分为初始化、运动模型、EKF实现、绘图和误差输出五个部分。初始化部分设置了时间序列、噪声协方差矩阵和状态矩阵；运动模型模拟了真实状态和观测值的变化；EKF部分实现了预测和更新步骤；绘图部分展示了滤波前后的状态量、误差曲线及误差累积分布；误差输出部分计算了滤波前后的最大误差值。运行结果通过图表展示了滤波效果，代码可通过链接下载。
极限学习机进行电厂相关数据预测
leo__520的博客
05-13 874
使用极限学习机（Extreme Learning Machine, ELM）进行电厂相关数据预测的详细步骤和MATLAB代码示例。假设任务是预测电厂发电量或设备状态（如温度、压力），代码包含数据预处理、ELM模型构建、训练与预测全过程。其中，(\mathbf{H} = g(\mathbf{X} \mathbf{W}_{\text{hidden}} + \mathbf{b})) 为隐层输出，(g) 为激活函数（如Sigmoid、ReLU）。通过调整隐层节点数、激活函数和正则化参数，可优化模型性能。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值