五连杆VMC

最近在搞这部分的理论，以便后续应用到实践上。文章参考五连杆运动学解算与VMC - 知乎 (zhihu.com)

A、E两转动副由电机驱动。

A、E的转动角度可通过电机编码器测得。

VMC控制任务中主要关注五连杆机构末端C的位置，通常可用直角坐标（x，y）或极坐标表示。

ps：极坐标是是指用角度和长度描述位置的坐标系统。

在这个系统中，一个点的位置由两个参数决定：极径（即点到原点的距离）和极角（即从固定方向到连接点与原点的直线之间的角度）。

通过五连杆左右两部分列写 C 点坐标，可得到以下等式：

求解方程组可得到角度 ϕ2 ：

其中：

 

ps：

1、

这个公式计算了从点 B 到点 D 在 x 轴方向上的距离的两倍，乘以长度 

2、同理

3、

根据余弦定理

4、

 根据两点间距离公式

通过角度 ϕ2 即可解算出 C 点直角坐标 (x,y)：

进而得到极坐标 (L0,ϕ0)：

VMC

虚拟模型控制（Virtual Model Control，简称VMC）算法是一种用于机器人，特别是四足机器人运动控制的方法。它通过在控制对象上假设存在虚拟元件如弹簧和阻尼器等，分析控制对象所受的虚拟力，并通过雅可比矩阵建立虚拟力和关节力的映射关系，从而实现对机器人的控制。

这里的全微分被用来描述被用来描述五连杆两个末端四个电机的位置和姿态如何随着关节角度的变化而变化。如果我们有一个机器人的正运动学模型 x=f(q)，其中 x 表示末端执行器的位置和姿态，q 表示关节角度，那么我们可以通过对 f 求全微分来得到雅可比矩阵：

即：

雅可比矩阵 J 将关节速度 q 映射为末端执行器的姿态变化率 x

ps：全微分用于描述多变量函数在一点处的线性变化。对于一个多变量函数，全微分可以告诉我们当输入变量发生微小变化时，函数输出将如何变化。

ps：虚功原理是是指在力学系统中，当系统处于平衡状态时，所有外力所做的虚功之和为零的原则。在本文五连杆中，虚功原理被用来建立关节速度与连杆姿态变化率之间的关系，进而解算出关节电机输出力矩。

但对上文推导出的正运动学模型直接求取雅可比矩阵 J 并不是好办法，因为模型表达式中包含大量平方与三角函数及其嵌套运算，直接调用符号运算工具的求雅可比矩阵函数会得到极其复杂的结果，无法转移到嵌入式平台进行计算，故需要通过其他方法来计算。

根据可知，雅可比矩阵 J 实际描述的是两坐标微分的线性映射关系，因此我们可以通过计算速度映射关系来得到雅可比矩阵。

对求导可得：

其中 ϕ1 可由电机编码器测得。

对式

求导可计算 ϕ2：

消去 ϕ3 求得 ϕ2：

其中：

代入进去就能得到ϕ2。

再将 ϕ2 代入式 即可得到：

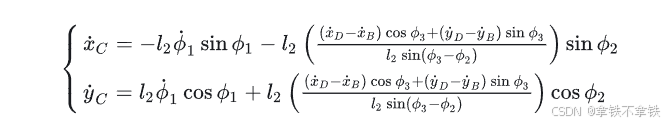
可以看到，通过这种方法计算的公式不再包含平方与三角函数嵌套运算，三角函数之间的加减乘除也可以利用两角和差公式进一步化简。

 

 

 

 向大佬学习（南方科技大学韭菜的菜）