特征法建树的千层套路

简说基因-专业生信合作伙伴

于 2025-02-07 20:52:07 发布

阅读量403

点赞数 4

本文链接：https://blog.csdn.net/weshengxin/article/details/145505885

版权

特征法建树，顾名思义就是直接运用序列特征来构建系统发生树。不同于距离法，它并不会将序列特征先转换为距离矩阵，再构建系统树，故对于单个位点中包含的进化信息，特征法可以做出更加充分的使用。目前流行的特征法有最大似然法（Maximum-likelihood, ML）、最大简约法（Maximum-Pasimony, MP）和贝叶斯推断（Bayesian Inference, BI）。

今天，我们不具体介绍三种特征法的具体软件操作方法，而关注它们的算法原理。这可以帮助我们在理解的基础上更好地在具体情境中选择最适的方法。

算法原理

最大简约法：最小进化，最大简约！

最大简约法，顾名思义，就是要得到最“简约”的树。这里的“简约”指的是树枝长的最简，即：得到似然树需要经历的特征进化步骤最小。这个原理基于最小进化的假设，咋一听似乎很简单——确实很简单。不过，要真正从大规模数据集构建最大简约树是一件非常费劲的事。

理想状态下，我们似乎可以通过特征将样本进行归类，比如：对于“骨骼”这一个特征，很明显，人、乌龟、鸟、蝙蝠有骨骼，是一类；蟑螂和草履虫没有骨骼，是一类；对于“多细胞”这个特征，人、乌龟、鸟、蝙蝠和蟑螂是一类，草履虫是一类；对于“哺乳”这一特征，人、蝙蝠是一类，乌龟、鸟、蟑螂和草履虫是另一类。那么，根据最大简约的原则，它们的进化关系就是：

如果引入更多特征，我们则可以构建出更加完善的进化树：

这听起来很简单，似乎人人都能根据这种二歧分类的思想快速构建出最大简约树。然而，我们如果仔细思考一下这个问题，就会发现：鸟也有翅膀啊，蝙蝠也有翅膀啊，那是人和鸟的关系最近呢？还是人和蝙蝠的关系最近呢？

根据我们积累的知识，我们知道蝙蝠和鸟的翅膀并不是同源的。它们是趋同进化的结果。所以，蝙蝠和鸟的翅膀并不能算有进化意义的共同特征；而且，仔细观察就会发现，蝙蝠和鸟都有翅膀，但是蝙蝠的翅膀覆盖的是肉膜，鸟的翅膀覆盖的是羽毛；蝙蝠和鸟的翅膀的骨骼结构也不一样；如果纳入更多特征来考虑的话，蝙蝠和人的共同特征更多，鸟和人的共同特征更少……总之，最终仍然能得出结论，蝙蝠和人的关系更近。

在DNA的进化上，这一点也是相同的：同一个位点只有A/T/C/G四种可能，它的进化路径可以是A->T，也可以是A->T->A（回复突变），还可以是A->G->T（多重突变），这就显得最大简约原则十分欠考虑（这也是最大简约法，乃至目前的大部分方法的一大缺陷）。更致命的是，分子趋同不是稀罕的事。处理DNA矩阵，并不会拿到理想的数据，而是庞大的数据集和复杂的情况。在这种情况下，让人或电脑一眼看出最大简约树显然是不妥的。于是，需要引入可行的方法，以提供一个恰当的切入点和执行路径：树搜索。

树搜索

例如，对于刚刚的5个物种，我们可以先构建他们的一棵距离树（这棵树或许离简约树比较近，毕竟它们都是基于最小进化原则的）或者一棵随机树，然后我们不断地改进树的结构，让它的枝长不断变小，最终或能搜索出最大简约树。

这需要我们按照一定规律对树拓扑进行恰当的枚举，以获得新的拓扑，然后评估新的拓扑的总枝长……如此循环，搜索出简约树。系统树并不是简单的数值。基于目前的拓扑产生新拓扑的方法主要有3种：最近邻交换（NNI）、子树修剪重接枝（SPR）和二分重连接（TBR）。

最近邻交换（Nearest Neighbor Interchange, NNI）

这是相对最快速、改变拓扑较小的一种方法：选中树中的一条边，从它的两侧任选一个子树节点互换位置。如果我们给刚才构建的简约树进行一次NNI，那么可以是这样：

可以看出，NNI还是有缺陷的：如果要完成人和草履虫在拓扑上的位置对调，需要进行很多次NNI。不急，我们还有其他的方法。

子树修剪重接枝（Subtree Pruning and Rerooting, SPR）

这种方法可以单次更大程度地改变树拓扑，其原理十分容易理解：从系统树上随机剪下一条枝条，然后将其重新插入到另一个枝条上：

SPR可以达到NNI的效果。如果我们剪下乌龟这个子树，将其插入到蟑螂与草履虫的枝条上，那么就等效于完成了刚才的NNI。

二分重连接（Tree Bisection and Reconnection, TBR）

这种方法对树拓扑的改变更大。它也是通过剪断一个枝条将一棵树分为两个子树，然后在两个子树上任选两个枝条引入新节点，并将这两个节点连接。相对于SPR，TBR不仅可以一次性完成大量的树拓扑的更改，还会同时改变两个子树的共同祖先情况：

算法优化

但是，如果我们仅采用以上这些方法来列举拓扑，并计算它们的枝长，那么数据量随样本量的增加并不是计算机能承受的：如果样本数量直线上升，那么树的数量则呈指数上升。当样本量为3时，二叉无根拓扑为1；4时为2；5时为12……很快，等到到达常用的数据量后，穷举搜索最大简约树就好比在足球场中找一棵乒乓球。

于是就有了一些优化的方法，比如TNT采用的启发式搜索等方法。其原理在此就不多介绍；效果就是：PAUP*4使用单纯的NNI搜索一晚上都无法找到的最大简约树，使用TNT或许只需要数分钟。当然，这些方法肯定是有局限性的。在保证速度的同时无法遍历所有可能的树拓扑，导致最终的搜索结果可能是极大简约树（局部最优解），而不是最大简约树。

最大似然法：贪婪的爬山之旅

在核酸进化上，简约法仅考虑发生进化次数最少，却不能区分碱基的替换和颠换。但我们知道，实际情况下，碱基替换与颠换的频率是不同的，替换远比颠换容易，且这个频率可以由先前的一些观察经验式地总结出来。于是，另两种运用碱基替换模型的特征法：最大似然法（ML）与贝叶斯推断（BI）应运而生。

相同地，最大似然法与最大简约法一样，也尝试寻找一个全局最优解。然而，评估最优解的方法这次不是总枝长，而是似然值。似然值纳入了更多因素，包括对不同碱基替换频率的考量。所以，最大似然法可以说是加入了一部分经验上的东西，对最优解做了更实用、更精确的定性。碱基的替换频率等等经验因素被纳入树拓扑的考量，会影响到最优解的定性。正是因此，最大简约树不需要碱基替换模型，而最大似然法和贝叶斯推断需要碱基替换模型且对模型很敏感。

在一个数据集可能产生的所有树拓扑中，分布着似然值较大的拓扑和似然值较小的拓扑。最大似然法的策略就是：通过不断地对现有的树的拓扑进行更改（方法仍然是上述的NNI、SPR、TBR），不断提高树的似然值，最终在似然值最大时得到最大似然树。

这个策略理解起来就是：有个人想要从山脚爬上山顶（山顶就是最大似然树），于是他每一步都朝着更高的地方走（提高似然值），最终就会到山顶上。

但是这个方法也有问题：万一在山的边上有一座小土丘，这个人最终爬到土丘的顶上呢？——这个问题最大似然树也会遇到：和最大简约树一样，最大似然树有时会搜索出一个局部最优解（极大似然树），而不是全局最优解：

在这种情况下，一方面，我们可以采取TBR这样的搜索策略，对原先的拓扑进行更加完全的打乱，让这个登山的人看的更远一些：在评估下一步往哪走的时候，能看到远处的山坡，而不是只看到脚下的两块石头。但是，这种方法往往也伴随着运算量的大幅增加。于是，另一些搜索策略出现了：

更改初始树类型，找个好点的位置开始登山

登山者总得有一个出发点。在开始搜索的时候，我们也要和最大简约树的搜索一样，指定一个拓扑作为树的搜索起点，称为初始树。如果这棵树就在最大似然树的附近（登山者从最高峰的山脚或者半山腰开始登山），那么我们就可以保证最终的结果就是最大似然树；如果这棵树与最大似然树的拓扑一致（登山者直接出生在山顶上），那岂不美哉？

目前使用的初始树类型大多为随机树、邻接树（NJ）、BioNJ、简约树。后三者可能较为靠近最大似然树，而前者的范围大，可能探索到其他几种初始树无法涉及极大区域。

设置多个初始树，人多力量大

一个登山者或许难以找到最高峰；那么，两个人在不同的区域找呢？3个人呢？20个人呢？抱着这样的思路，我们也可以对最大似然树同时进行多个搜索，分别从不同的初始树开始，最后评估一下谁的结果似然值更大，这样就有更大的概率找到最大似然树。

对每个节点进行置信度评估，从而对症下药地优化树结构

如果我现在给你这样一棵系统树：

相信你能很快地发现其中的问题：草履虫与乌龟的进化位置不对！这两个枝条有问题，应该进行一次NNI把两者对调，才能找到真正的进化关系。那么恭喜你，已经大概明白了节点置信度评估的目的。

在初始地得到一个似然值较大的树拓扑之后，我们可以检验每一个枝条。如果这个枝条（也可以理解为它两侧的子树/它的两个节点）呈现的进化关系有问题，拉低了总体的似然值，我们就对症下药地使用NNI/TBR/SPR从它入手优化整棵树，从而提升整体的似然值，向最大似然树靠近。

要察觉到问题节点，我们就需要向计算机量化地提供每个节点的置信数值：它是不是已经最优了？由于这个数值通过抽样重新检验产生，代表不同的随机抽样对其表现出支持的百分数，所以它被称为支持率（support value）。检验的方法分为两种：Bootstrap法（自展法，亦称自举法、靴摩法【这名字真文艺】）和Jackknife法（刀切法）。两者都是从样本的序列比对中割下若干块局部的比对，观察每个局部中的位点是否支持当前树的某个节点，最终根据百分比生成每个节点的支持率。不同点是，Bootstrap是放回的随机抽样；Jackknife是不放回的随机抽样。因此，bootstrap一般产生比jackknife更多的局部，更加费时费力，但也能收获比Jackknife更加精确的检验结果。除此之外，还有SH-LRT、aBayes等评估方法，这里不多赘述。

一起来分析IQTree的运行日志

笔者从他的系统发育结果中找到了一份IQTree的运行日志。接下来让我们看看上述的搜索策略在实际情况中是怎么进行的。（......为笔者人工略去的部分。整个日志实际上非常长）

首先，IQTree通过传递给它的参数导入了相关的序列比对，识别了其中的所有位点：

IQ-TREE multicore version 2.2.0 COVID-edition for Windows 64-bit built Jun  1 2022
Developed by Bui Quang Minh, James Barbetti, Nguyen Lam Tung,
Olga Chernomor, Heiko Schmidt, Dominik Schrempf, Michael Woodhams, Ly Trong Nhan.
......
Alignment most likely contains DNA/RNA sequences
Constructing alignment: done in 0.0172768 secs using 90.44% CPU
Alignment has 49 sequences with 12175 columns, 9244 distinct patterns
8959 parsimony-informative, 737 singleton sites, 2479 constant sites

然后，它根据IQ_partition.txt（分区文件）识别了所有的分区以及为分区提前指定的替换模型：

Loading 29 partitions...
Subset    Type    Seqs    Sites    Infor    Invar    Model    Name
1    DNA    49    595    413    133    GTR+F+I+I+R4    atp6_mafft_gb_codon1_cytb_mafft_gb_codon1
......
29    DNA    49    628    485    84    GTR+F+R4    rrnS_mafft_gb
Degree of missing data: 0.000

接着，它生成了一棵初始的简约树，为超快自举（ultrafast bootstrap）提前生成了随机采样（这也是一种运算优化策略）：

Info: multi-threading strategy over partitions
Create initial parsimony tree by phylogenetic likelihood library (PLL)... 0.046 seconds
Generating 10000 samples for ultrafast bootstrap (seed: 71425)...
NOTE: 439 MB RAM (0 GB) is required!
Estimate model parameters (epsilon = 0.100)
Initial log-likelihood: -353435.716

它对初始树完成了一些搜索，初步提升了它的似然值，然后又生成了另一种初始树：RapidNJ树，并计算了它的似然值：

Current log-likelihood at step 1: -334223.002
Current log-likelihood at step 2: -331304.439
Current log-likelihood at step 3: -330649.636
......
Current log-likelihood at step 57: -330062.719
Current log-likelihood at step 58: -330062.604
Current log-likelihood at step 59: -330062.510
Partition-specific rates:  0.300 0.119 1.802 0.627 1.767 1.822 0.134 0.029 4.760 0.202 0.079 4.523 0.212 0.080 3.137 0.101 0.362 0.101 2.369 0.469 0.160 0.191 0.156 2.202 0.155 0.382 1.485 0.373 0.327
Parameters optimization took 58 rounds (20.329 sec)
Wrote distance file to...
Computing ML distances based on estimated model parameters...
Calculating distance matrix: done in 0.0001942 secs
Computing ML distances took 0.000305 sec (of wall-clock time) 0.000000 sec (of CPU time)
Setting up auxiliary I and S matrices: done in 0.000145 secs
Constructing RapidNJ tree: done in 0.0014289 secs
Computing RapidNJ tree took 0.001714 sec (of wall-clock time) 0.000000 sec (of CPU time)
Log-likelihood of RapidNJ tree: -406507.620

接着，它又在先前的基础上生成了另外98棵简约树，构成了一个100棵树的初始树集合，并保留其中的20棵似然值较大的树进行随后的正式搜索：

|             INITIALIZING CANDIDATE TREE SET                      |
Generating 98 parsimony trees... 7.863 second
Computing log-likelihood of 98 initial trees ... 4.250 seconds
Current best score: -330062.510
Do NNI search on 20 best initial trees
Optimizing NNI: done in 4.42811 secs using 307.7% CPU
Estimate model parameters (epsilon = 0.100)
Initial log-likelihood: -329912.880
Current log-likelihood at step 1: -329909.218
Current log-likelihood at step 2: -329908.745
Current log-likelihood at step 3: -329908.500
Current log-likelihood at step 4: -329908.340
Current log-likelihood at step 5: -329908.200
Current log-likelihood at step 6: -329908.110
Parameters optimization took 5 rounds (2.562 sec)
BETTER TREE FOUND at iteration 1: -329908.110

从日志中可以看出，IQTree使用的搜索方式是NNI。这是最快捷的搜索方式，在本身的初始树集已经比较大的情况下，这种策略也进一步提升了搜索速度。

使用NNI对初始树集进行快速的似然值提升，总共进行了20次迭代：

Optimizing NNI: done in 7.77645 secs using 318.9% CPU
Optimizing NNI: done in 7.70476 secs using 417.4% CPU
Optimizing NNI: done in 7.41412 secs using 439.4% CPU
Optimizing NNI: done in 6.68376 secs using 469% CPU
Optimizing NNI: done in 9.04357 secs using 455.8% CPU
Optimizing NNI: done in 8.95789 secs using 419.7% CPU
Optimizing NNI: done in 7.99221 secs using 413.9% CPU
Optimizing NNI: done in 7.15394 secs using 396.9% CPU
Optimizing NNI: done in 9.60568 secs using 403.4% CPU
Iteration 10 / LogL: -329908.162 / Time: 0h:1m:58s
Optimizing NNI: done in 8.92868 secs using 403.9% CPU
Optimizing NNI: done in 8.65517 secs using 406.7% CPU
Optimizing NNI: done in 8.44464 secs using 392.3% CPU
Optimizing NNI: done in 7.81354 secs using 394.7% CPU
Optimizing NNI: done in 9.08831 secs using 404.5% CPU
Optimizing NNI: done in 7.47969 secs using 437.9% CPU
Optimizing NNI: done in 7.5994 secs using 425.2% CPU
Optimizing NNI: done in 6.46172 secs using 515.5% CPU
Optimizing NNI: done in 8.07937 secs using 528.2% CPU
Optimizing NNI: done in 9.1261 secs using 415.4% CPU
Iteration 20 / LogL: -329908.401 / Time: 0h:3m:20s
Finish initializing candidate tree set (2)
Current best tree score: -329908.110 / CPU time: 173.422
Number of iterations: 20

完成初始化后在随后的迭代中结合NNI与超快自举，对树结构进行快速的优化。（笔者注：这种迭代式的自举方式可以看作一种启发式搜索，自动根据数据集的复杂程度个性化自举检验的方案）同时，也在不断修正GTR替换模型中具体的替换频率：

|               OPTIMIZING CANDIDATE TREE SET                      |
Optimizing NNI: done in 2.31044 secs using 369.9% CPU
Optimizing NNI: done in 1.82863 secs using 380.2% CPU
Optimizing NNI: done in 1.28146 secs using 349.9% CPU
Optimizing NNI: done in 1.01487 secs using 301.8% CPU
Optimizing NNI: done in 1.09342 secs using 410.1% CPU
Optimizing NNI: done in 0.609933 secs using 286.9% CPU
Optimizing NNI: done in 1.64574 secs using 330.4% CPU
Optimizing NNI: done in 0.822953 secs using 307.6% CPU
Optimizing NNI: done in 1.97317 secs using 350% CPU
Optimizing NNI: done in 1.93073 secs using 354.5% CPU
Iteration 30 / LogL: -329908.360 / Time: 0h:3m:35s (0h:8m:46s left)
......
Optimizing NNI: done in 1.3864 secs using 352.8% CPU
Optimizing NNI: done in 0.644048 secs using 291.1% CPU
Optimizing NNI: done in 1.66316 secs using 362.6% CPU
Iteration 100 / LogL: -329908.163 / Time: 0h:5m:17s (0h:0m:3s left)
Log-likelihood cutoff on original alignment: -330005.407
NOTE: Bootstrap correlation coefficient of split occurrence frequencies: 1.000
Optimizing NNI: done in 1.59078 secs using 371.3% CPU
Optimizing NNI: done in 2.36801 secs using 406.5% CPU
TREE SEARCH COMPLETED AFTER 102 ITERATIONS / Time: 0h:5m:23s
|                    FINALIZING TREE SEARCH                        |

将最终选定的碱基替换频率应用到结果上。搜索出了最优替换频率，其实相当于得到了最大似然树：

Performs final model parameters optimization
Estimate model parameters (epsilon = 0.010)
Initial log-likelihood: -329908.110
Current log-likelihood at step 1: -329908.037
Current log-likelihood at step 2: -329907.972
......
Current log-likelihood at step 44: -329904.861
Current log-likelihood at step 45: -329904.851

为每个节点的自展支持率，生成合意树，并存储结果：

Partition-specific rates:  0.295 0.117 1.781 0.616 1.753 1.796 0.133 0.028 4.988 0.199 0.080 4.507 0.210 0.081 3.116 0.098 0.355 0.098 2.335 0.463 0.159 0.187 0.156 2.151 0.151 0.376 1.457 0.366 0.322
Parameters optimization took 44 rounds (10.405 sec)
Partition information was printed to ......
BEST SCORE FOUND : -329904.851
Creating bootstrap support values...
Split supports printed to NEXUS file ......
Total tree length: 43.673
Total number of iterations: 102
CPU time used for tree search: 1100.578 sec (0h:18m:20s)
Wall-clock time used for tree search: 296.853 sec (0h:4m:56s)
Total CPU time used: 1164.234 sec (0h:19m:24s)
Total wall-clock time used: 335.821 sec (0h:5m:35s)
Computing bootstrap consensus tree...
Reading input file ......
49 taxa and 156 splits.
Consensus tree written to ......
Reading input trees file ......
Log-likelihood of consensus tree: -329904.852
Analysis results written to:
IQ-TREE report:                ......
Maximum-likelihood tree:       ......
Likelihood distances:          ......
Ultrafast bootstrap approximation results written to:
Split support values:          ......
Consensus tree:                ......
Screen log file:               ......
Date and Time: Mon Jan 20 18:08:46 2025

最终得到了最优树，也就是搜索到的最大似然树；以及合意树，对应MEGA中的Original tree和Bootstrap consensus tree。这两棵树本身是相近的，合意树由于有着更大的样本量的支撑，可能可以避免一些偶然性的干扰。

贝叶斯推断：不断总结经验的爬山之旅

现在有个聪明人。他不再根据肉眼可见的“最高点”来爬山，而是掌握了一个复杂的计算方法，可以根据自己目前的处境，推算出下一步的走法，然后再依次推断出下下步的走法。。。如此，找到最优解。是不是听起来很魔幻？这就是贝叶斯推断的核心。

“三门问题”是经典的贝叶斯统计问题。参赛者面对三扇关闭的门，其中一扇门后有汽车，另外两扇门后各有一只山羊。参赛者首先选择一扇门，然后主持人会打开剩下两扇门中的一扇，并展示一只山羊。此时，参赛者可以选择是否更换自己的初始选择，从而提升获奖的概率。在这个问题上，传统统计学与贝叶斯统计产生了分歧。传统统计学认为更换选择不会影响获奖概率；而贝叶斯统计则根据条件概率，根据观测到的结果对初始的估计进行优化。这便是“先验概率”与“后验概率”的思想。如果把爬山比作一个概率问题，我们在选择了出发点（初始树，先验概率）后，可以通过结合当前的处境估计下一步（后验概率），走到下一步的位置（用后验概率修正先验概率）之后再观察考量（生成新的后验概率）……这种不断总结经验、修正误差的树搜索方式即为贝叶斯推断。

由于贝叶斯推断背后涉及复杂的统计学知识，我们在此处便不多赘述，而专注于它的实现原理。

我们发现，这种树搜索的方式表面上完全根据当前的处境计算后验概率，决定下一步的策略，而当前的处境其实又是根据上一步的处境所得的后验概率选定的。。。。这种无记忆性的统计学状态转移，不就是马尔科夫链么？

没错，贝叶斯推断就是通过马尔科夫链来解决问题。它通过不断用后验修正先验让马尔科夫链上的树拓扑和各项参数逼近最优解，并最终一直稳定在最优解附近。通过构建一个马尔科夫链，使得该链的平稳分布即为所求的目标分布。这种抽样技术称为马尔科夫链蒙特卡罗（MCMC）。贝叶斯推断最终得到一条趋近于全局最优解的MCMC。

如果不理解的话，结合下图：

左边的爬山经历的先验概率/后验概率变化，与右边的折线是对应的。这条折线被称为先验概率/后验概率的迹线图（Trace plot）。它是对应值在mcmc每一轮迭代中的值的变化趋势线。实际情况下，MCMC包括各个被纳入考虑的环境因素（也就是贝叶斯推断的各项可变参数），所以这些参数也有自己对应的迹线图。一轮贝叶斯推断得到两个数据集：一个是各个参数的在MCMC中的采样集，一个是树拓扑在MCMC中的采样集。

那么，如何处理这些数据呢？

预烧（burn-in）

MCMC从起始树和初始参数开始搜索更优的参数。到各项参数的迹线图最终稳定之前，这些取值和树拓扑无益于最终结果的提取。因此，在解析最终结果时，需要将MCMC未稳定的部分去掉不做讨论。这一步称为预烧。常见的预烧有10%、25%、50%等，也可以根据对MCMC的观测调整预烧。

预烧可以提前设置（MrBayes、BEAST等软件都有这个功能），也可以在MCMC完成后使用诸如LogCombiner的软件手动进行。

MCMC在最开始运行时会有一个不稳定的阶段，如图：

收敛性检验

MCMC稳定于某一个值，称为收敛。此时，迹线图的所有采样点在被统计后，应呈现出较为完美的分布曲线或直方图（对不连续量）。它可以近似正态分布、对数正态分布、两点分布、二项分布等等。评估收敛性可以通过上文所述的观察迹线图和分布的方法进行，也可以通过统计数值反映。常用的数值为有效样本量（Effective Sample Size, ESS）。软件Tracer专门用于分析MCMC。在其中可以查看迹线图、分布图，每项数值的ESS会被自动计算，且低于100的标红、低于200的标黄。一般来说，当ESS大于200时，我们认为某一参数已经收敛。对于未收敛的参数，可以通过延长MCMC、增加预烧来促进其收敛。

如图，收敛参数的迹线图和分布图。图中参数：LnL（似然值的对数）。预烧10%。

另一方面，树拓扑采样集的收敛性则反映为：一种拓扑在众多拓扑中占有绝对的优势。这一点有时可以通过似然值、后验概率、先验概率及其衍生量（对数值、负对数值等）收敛来体现，但是，对于这些值相近的拓扑而言是无效的。这时，我们可以对树集进行可视化，从而检查拓扑的一致性。这一可视化可以使用DensiTree来完成。

如图：Densitree的树集可视化结果。几组相异的主流拓扑会被软件自动使用不同颜色标记（引自Ye 2024。DOI: 10.24272/j.issn.2097-3772.2024.007）：

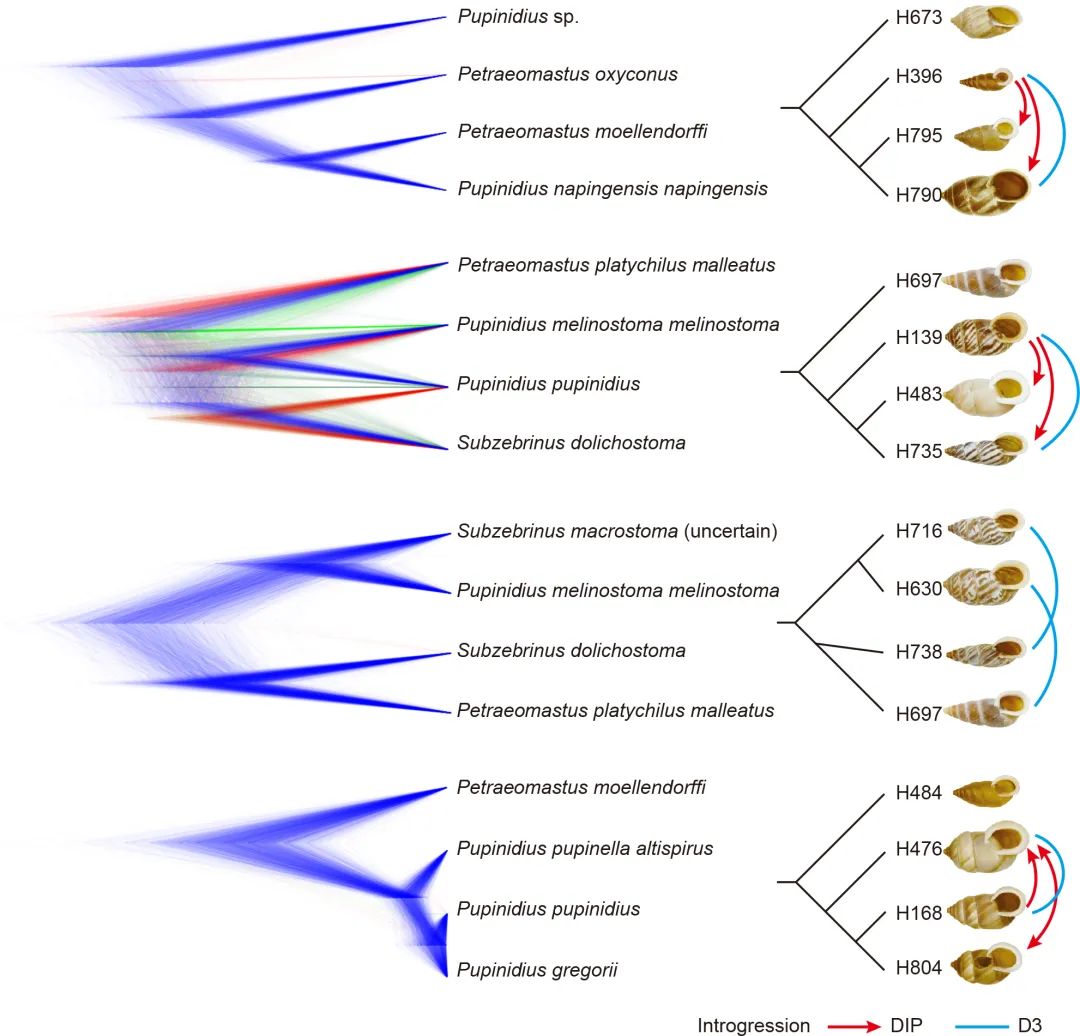
树集的整合

欲要将树集变为最终的BI树，则需要使用一定方法对其进行整合，将几万个拓扑的关键特征压缩到一棵树上。目前，整合主要有这几类方法：

• 用户指定树（User target tree）：指定一种拓扑，软件从树集中寻找符合这种拓扑的所有采样，并把它们的枝长、后验概率等节点信息整合到这个拓扑上。可用TreeAnnotator实现。
• 最大进化枝可信度树（Maximum Clade Credibility Tree，MCC）：从树集中选出支持率最高的一个拓扑，类似于ML法中的original tree。由于MCMC中的收敛不是稳定在最优解上，而是在最优解附近跳动，用这种方法得到的树可能与最优解存在细微偏差。可用TreeAnnotator实现。
• 严格共识树（Allcompat Tree）：从树集中选出支持率最高的一组拓扑，并把它们所有节点信息整合后重新注释到上面。类似于ML法中的strict consensus tree。可用MrBayes实现。
• 50%多数一致树（Halfcompat Tree）：当多个输入树中存在冲突时，保留在多数输入树中一致的分支，而忽略那些只在少数输入树中出现的分支。这一整合方法允许将不同拓扑的高置信度部分拼凑整合，包容性更强。可用MrBayes实现。

MCMC运算速度的优化

有小伙伴如果用过MrBayes的话，就会发现它的一大缺点：慢！非常慢！一个数据量不大的数据集，用IQTree跑10000次超快自展的ML树只需要几分钟，用MEGA跑1000次自展检验的ML树，或许一两个小时就跑完了，但如果用MrBayes跑默认的2个独立运行、4条MCMC、200万代的贝叶斯推断，需要等上大半天。毕竟MCMC迭代次数远多于自展检验次数。即使单次迭代速度超过单次自展，总体的时间消耗也是巨大的。

然而，当你去使用BEAST1的时候，就会发现：同样的1000次迭代，BEAST1比MrBayes快了几倍；再去用BEAST2的时候，又会发现：BEAST2比BEAST1又快了几倍。

为什么呢？它们执行的不都是贝叶斯推断么？BEAST的参数集不是比MrBayes更庞大么？

因为BEAST软件包会在进行分歧时间分析前，要求你给它配置BEAGLE库。

MCMC的采样运算需要调用CPU或者GPU作为算力设备。而BEAGLE库的作用则是在这一过程中进行协调指挥，充分激发处理器的MCMC运算潜能。在此基础上，BEAST2相对于BEAST1，可以设置更多线程数和实例数，而且可以根据计算机本身的硬件情况，自动选择最优的算力设备，速度自然也提升了。

实际上，作为最常用的贝叶斯推断软件，MrBayes也可以配置BEAGLE库。在使用了BEAGLE加速后，其单线程运算速度显著大于相同数据集下的BEAST1，且紧追BEAST2。但坏消息是：Windows系统下的MrBayes不支持整合BEAGLE加速。

有些小伙伴可能感到不悦：自己用的就是Windows系统；实验室也没有Linux的服务器。但是办法总归是有的。笔者日常用的正是Windows系统，但需要进行贝叶斯推断时，是在WSL Ubuntu子系统中启动编译了BEAGLE的MrBayes，然后通过子系统访问存储于Windows目录中的数据块NEXUS文件进行贝叶斯推断。