纵向数据分析还在做交叉滞后？不如来看看这个——k-means designed to work specifically on longitudinal data

1.方法介绍

        目前在教育学和心理学的研究中出现了两种不同的观点，以变量为中心的观点(Variable-centred)提倡探究变量与变量之间的关系，例如很多横断面研究测量某个时刻参与率与成绩之间的关系。而以事件为中心的观点(event-centred)则认为学习不是一个静态的过程，参与率和学习成绩会随着时间发生动态变化，探索学习在特定时间点的输入和输出之间的因果关系是没有意义的。因此研究者需要在动态的时间变化中捕捉变量之间的联系。在这种情况下，KML(k-means designed to work specifically on longitudinal data)和KML3d(k-means designed to work specifically on longitudinal joint trajectories)应运而生。

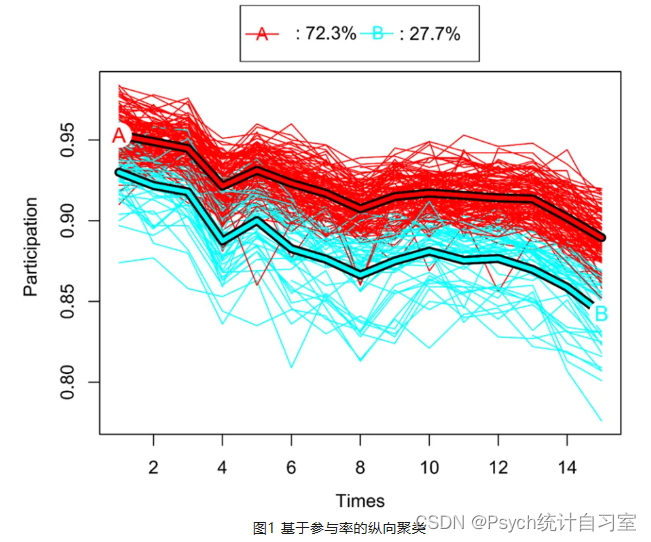
        KML和KML3d都是一种纵向聚类技术。即记录下某一个时间段内变量的纵向变化过程，然后基于一个(KML)或者多个(KML3d)变量的纵向轨迹进行聚类，最终得到了多种不同模式的纵向变化的分组。本期内容我们只介绍KML技术，有关KML3d的内容下期会介绍。如图1所示，研究者记录下一个学期(15次授课)中每节课的参与率，绘制了所有班级的参与率的纵向变化曲线，然后基于纵向轨迹进行聚类，区分出了两大类班级，一种是参与率持续走低的班级，一种是参与率普遍更高的班级。区分出班级之后呢，研究者就可以基于组别去进行一些其他的处理，例如比较两组的学习成绩等。

        之前的研究一致认为，KmL技术是一种成熟、可靠、更不耗时的纵向聚类方法。它首先应用于流行病学研究中的队列研究，然后逐步扩展到教育和心理学领域。KmL技术是一种使用k-means聚类纵向数据的方法，它不关注单一变量，而是涉及同质个体的轨迹。K-Means是一种EM（期望最大化）爬山算法。由于该算法不需要簇内的任何正态性或参数假设，它在数值收敛方面更鲁棒(翻译成人话就是更稳定)。更重要的是，在纵向数据的背景下，它不需要对轨迹的形状进行任何假设。自从Genolini & Falissard (2010)开发了基于R语言的KmL软件包以来，KmL技术得到了广泛的应用。 

2.统计原理

        Kml其实就是K-means聚类方法在纵向数据上的使用。K-means算法是一种非参数爬山算法，将n个具有p个变量的对象划分为k个同质子群(这个定义包含了KML3d，KML3d主要是基于多个变量的纵向轨迹进行联合聚类，由于当变量等于2个时，再加上时间轴，这就是一个3d图，如果再增加变量就是4维，我们很难通过图形表示出来)。通过利用KmL包，我们可以通过多次迭代获得最优的簇数及其轨迹。一个典型的KML的步骤包括以下步骤：

        1)定义了集群（种子）的初始中心。

        2)根据初始种子，得到对象与种子向量之间的距离。然后，每个观测结果都被分配到最近的集群中心。KmL可以使用欧几里德距离法(Euclidean distance method)和曼哈顿距离法(Manhattan distance method)。对于给定的n个对象的集合S，下图两个公式分别代表欧式距离（左）和曼哈顿距离（右）的计算方法：