2.3 可逆矩阵的特征（第2章矩阵代数）

内容概述

本节将可逆矩阵的概念和之前学到的一些概念进行了关联，说明了这些概念之间的等价性。最后以空间变换为例，讲述了逆矩阵和逆变换之间的联系。

可逆矩阵的特征

本节重点讲逆矩阵的概念和第一章中$n$个未知量$n$个方程的方程组以及方阵联系起来。
定理：

设$A$为$n\times n$矩阵，则下列命题是等价的，即对某一特定的$A$，它们同时为真或同时为假：
a. A是可逆矩阵
b. A行等价于$n\times n$单位矩阵
c. A有$n$个主元位置
d. 方程$A\mathbf{x}=0$仅有平凡解
e. $A$的各列线性无关
f. 线性变换$\mathbf{x}\to A\mathbf{x}$是一对一的、
g. 对${\mathbb{R}}^n$中任意$\mathbf{b}$，方程$A\mathbf{x}=\mathbf{b}$至少有一个解
h. $A$的各列生成${\mathbb{R}}^n$
i. 线性变换$\mathbf{x}\to A\mathbf{x}$把${\mathbb{R}}^n$映上到${\mathbb{R}}^n$
j. 存在$n\times n$矩阵$C$使$CA=\mathbf{I}$
k. 存在$n\times n$矩阵$D$使$AD=\mathbf{I}$
l. $A^T$是可逆矩阵

上述定理的等价性可以一一彼此证明，事实上，如果能够深刻理解之前学习的内容，这些结论是显而易见的，均是同一件事情的不同说法。

例：

应用可逆矩阵定理来判断$A$是否可逆
$$A=\left[\begin{array}{ccc}1& 0& -2\\ 3& 1& -2\\ -5& -1& 9\end{array}\right]$$

解：

$$A\sim \left[\begin{array}{ccc}1& 0& -2\\ 0& 1& 4\\ 0& -1& -1\end{array}\right]\sim \left[\begin{array}{ccc}1& 0& -2\\ 0& 1& 4\\ 0& 0& 3\end{array}\right]$$
由于$A$有3个主元位置，根据上述定理（c），$A$是可逆的。

一定要注意的是，虽然可逆矩阵定理将许多重要概念作了关联，但必须强调，可逆矩阵定理仅能用于方阵。

可逆线性变换

当矩阵$A$可逆时，方程$A^{-1}A\mathbf{x}=\mathbf{x}$可看作关于线性变换的一个命题：

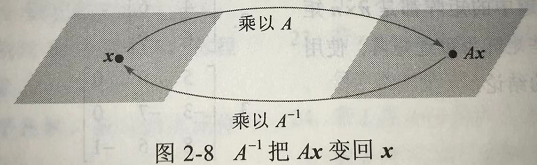
线性变换$T:{\mathbb{R}}^n\to {\mathbb{R}}^n$称为可逆的，若存在函数$S:{\mathbb{R}}^n\to {\mathbb{R}}^n$，使得：
对所有${\mathbb{R}}^n$中的$\mathbf{x}$，$S(T(\mathbf{x}))=\mathbf{x}$
对所有${\mathbb{R}}^n$中的$\mathbf{x}$，$T(S(\mathbf{x}))=\mathbf{x}$

下列定理说明若这样的$S$存在，则它时唯一的而且必是线性变换，我们称$S$是$T$的逆，把它写成$T^{-1}$。
定理：

设$T:{\mathbb{R}}^n\to {\mathbb{R}}^n$为线性变换，$A$为$T$的标准矩阵。则$T$可逆当且仅当$A$是可逆矩阵。这时由$S(\mathbf{x})=A^{-1}\mathbf{x}$定义的线性变换$S$是满足$S(T(\mathbf{x}))=\mathbf{x}$和$T(S(\mathbf{x}))=\mathbf{x}$的唯一函数。

证：

设$T$是可逆的，则$T(S(\mathbf{x}))=\mathbf{x}$说明$T$是从${\mathbb{R}}^n$映上到${\mathbb{R}}^n$的映射，因若$\mathbf{b}$属于${\mathbb{R}}^n$，$\mathbf{x}=S(\mathbf{b})$，则$T(\mathbf{x})=T(S(\mathbf{b}))=\mathbf{b}$，所以每个$\mathbf{b}$属于$T$的值域，于是由上述定理(i)，$A$为可逆的。
反之，若$A$是可逆的，令$S(\mathbf{x})=A^{-1}\mathbf{x}$，则$S$是线性变换，且显然$S$满足$S(T(\mathbf{x}))=\mathbf{x}$和$T(S(\mathbf{x}))=\mathbf{x}$。例如：$S(T(\mathbf{x}))=S(A\mathbf{x})=A^{-1}(A\mathbf{x})=\mathbf{x}$。于是$T$是可逆的。

例：
设$T:{\mathbb{R}}^n\to {\mathbb{R}}^n$是一对一线性变换，则$T$会如何？
解：

$T$的标准矩阵$A$的列是线性无关的，所以根据可逆矩阵定理，$A$是可逆的，而且$T$把${\mathbb{R}}^n$映上到${\mathbb{R}}^n$，所以，$T$为可逆。

思考

可逆矩阵有两大特性：

• 可逆矩阵一定是方阵
• 可逆矩阵对应的线性方程存在唯一解

正是这两个特性，让可逆矩阵和之前学到的一些概念很好的关联了起来，例如主元位置、线性无关、空间变换等等概念，线性代数中一个主要的任务就是寻找不同概念之间的等价性。