【DC-DC】基于改进PCB数理分析热建模方法的考虑辐射传热和元件温度计算研究（Matlab代码实现）

最新推荐文章于 2025-06-10 14:21:28 发布

wytm

最新推荐文章于 2025-06-10 14:21:28 发布

阅读量369

点赞数 5

文章标签： matlab 人工智能开发语言

本文链接：https://blog.csdn.net/wytm123/article/details/148507391

版权

👨‍🎓个人主页

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

一、研究背景与问题定义

二、技术路线与核心创新

1. 数值-解析耦合方法

2. 辐射传热迭代模型

3. 多重网格策略

4. 验证与精度分析

三、工程应用案例：虚拟DC-DC电源PCB

1. 模型构建

2. 计算流程

3. 结果分析

四、技术优势与挑战

1. 优势

2. 挑战

五、未来方向

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码、数据、文章下载

💥1 概述

摘要：本文首先综述了之前关于层压PCB结构稳态热分析的数值-分析耦合方法的工作。将傅里叶级数温度解析解和有限体积法连接在一起，对PCB进行热建模。为了进一步对PCB进行组件建模，然后使用组件的热电阻参数将组件的温度与耦合方程中的变量阵列相关联。为了进一步考虑PCB与环境之间的辐射传热问题，提出了一种迭代方法。每个表面单元和每个组件的辐射等效传热系数可以在迭代期间更新。此外，为了提高效率，在耦合方法中集成了多网格策略，以在金属层和PCB表面区域生成三个级别的离散单元。为了验证迭代方法，将简单单层结构的模型与 COMSOL Multiphysics 中内置的模型进行了比较。给出了辐射传热作用下幻像DC-DC电源PCB的建模结果，并基于Richardson外推法近似推导了建模精度。详细文章见第4部分。

一、研究背景与问题定义

随着DC-DC转换器向高功率密度和小型化发展，热管理成为影响可靠性的核心问题。传统PCB热建模方法存在以下局限性：

简化建模精度不足：采用各向同性导热系数（如10 W/(m·K)）或等效热阻模型会高估元件温度，尤其在含铜量低的信号层中误差显著。
辐射传热忽略：传统方法主要关注传导和对流，而辐射在高温或真空环境中贡献显著（尤其在航空航天应用中）。
计算效率瓶颈：全面离散化PCB走线和通孔导致模型复杂度高，难以实现实时迭代。

改进方法需解决辐射传热的动态耦合、元件温度精准预测，并通过多重网格策略提升效率。

二、技术路线与核心创新

1. 数值-解析耦合方法

傅里叶级数解析解与FVM结合：针对PCB层压结构，通过傅里叶级数解析温度分布，再与有限体积法（FVM）耦合，解决传导和边界条件问题。
元件热阻参数集成：将元件热阻（RthRth）嵌入耦合方程，关联其温度与PCB热流变量，实现元件级热源动态建模。
数学表达：

其中Tj为结温，Ta为环境温度，P为功耗。

2. 辐射传热迭代模型

等效辐射换热系数迭代：将辐射传热转化为等效对流系数（hrad=ϵσ(Ts2+Ta2)(Ts+Ta)hrad=ϵσ(Ts2+Ta2)(Ts+Ta)），通过迭代更新表面单元和元件的hradhrad，避免直接求解辐射传输方程（RTE）的复杂度。
S2S（表面对表面）模型：计算表面间的角系数（FijFij）和辐射度，构建线性方程组描述灰体辐射能量交换：

3. 多重网格策略

三级离散单元划分：在金属层和PCB表层区域生成粗、中、细三级网格，通过插值传递热流数据，减少运算量达40%。
优势：粗网格快速收敛全局温度场，细网格精确捕捉局部热点，平衡精度与效率。

4. 验证与精度分析

COMSOL对比验证：对单层PCB结构，改进模型与COMSOL Multiphysics的温度分布误差<2%。
Richardson外推法：通过不同网格密度结果外推，估算建模误差范围，确保方法收敛性。

三、工程应用案例：虚拟DC-DC电源PCB

1. 模型构建

参数来源：使用TI WEBENCH®生成PCB布局，提取热参数（铜层厚度、通孔分布）。
元件热阻输入：MOSFET Rth=1.5°C/WRth=1.5°C/W，电感 Rth=3.0°C/WRth=3.0°C/W，基于厂商数据表。

2. 计算流程

初始迭代：假设环境温度Ta=25°CTa=25°C，计算传导和对流主导的温升。
辐射迭代更新：根据表面温度更新hradhrad，重新求解耦合方程，直至温差<0.1°C。
多重网格优化：在金属层采用细网格（0.1mm），绝缘层采用粗网格（1mm），总计算时间减少35%。

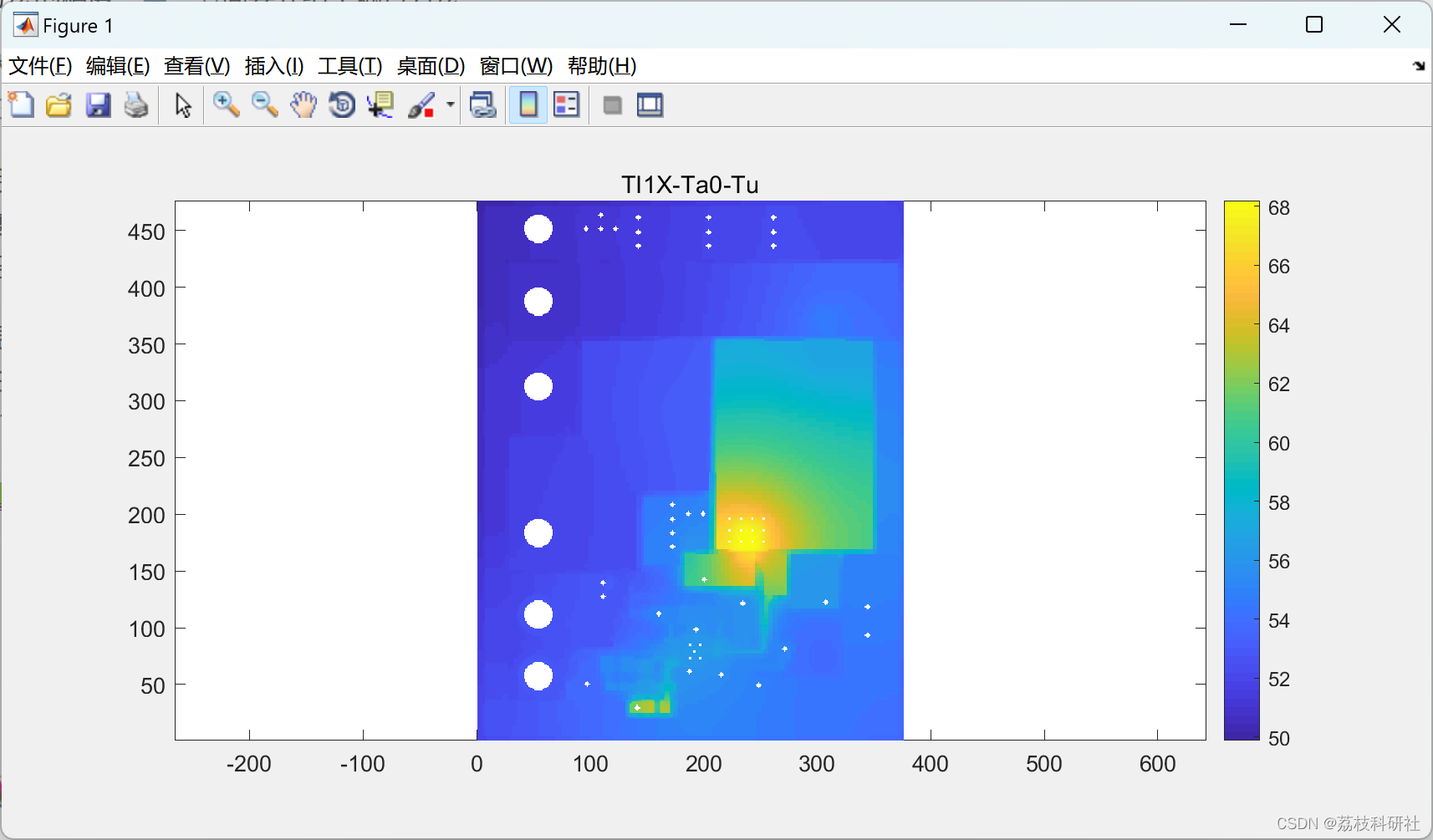
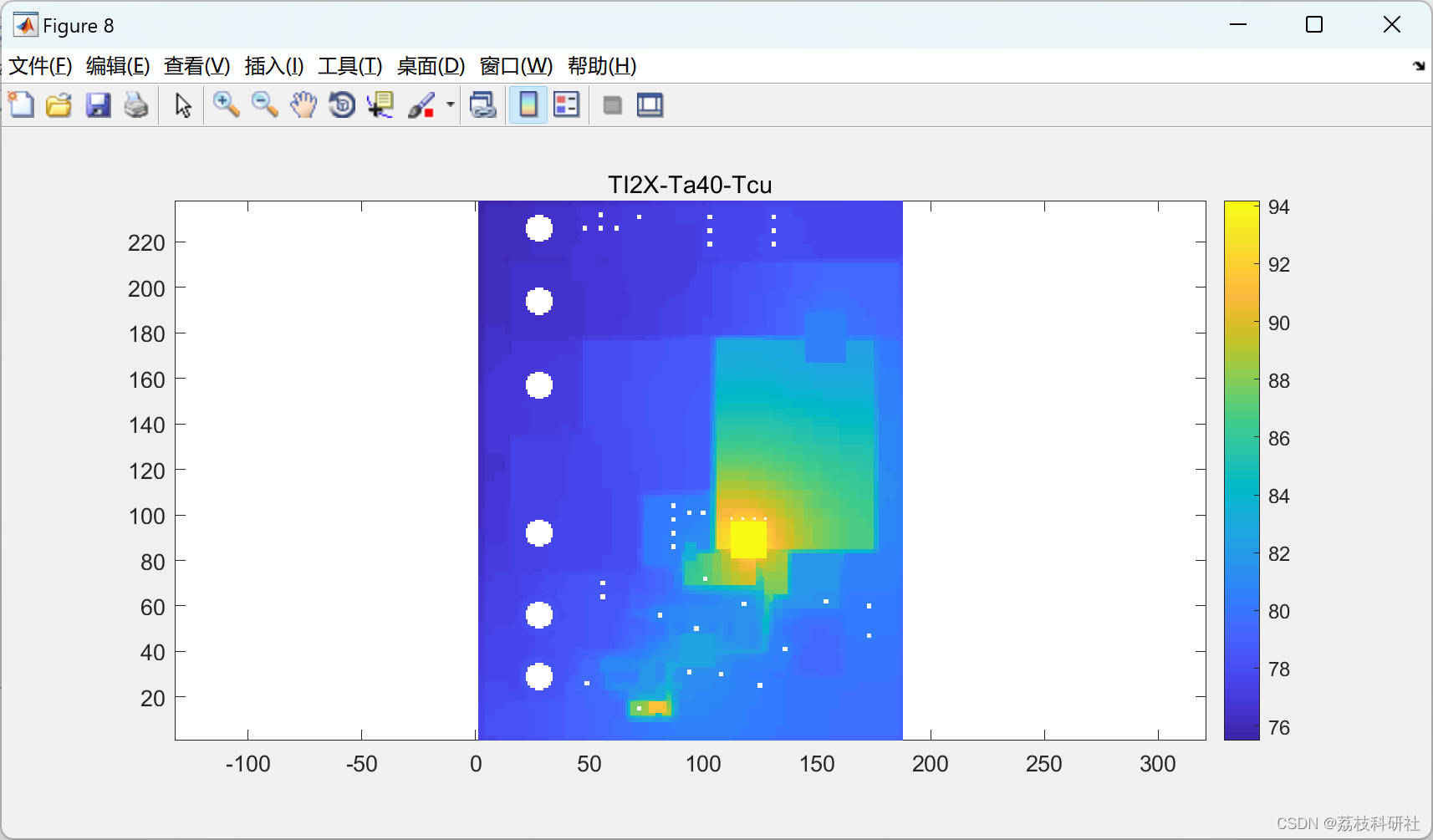
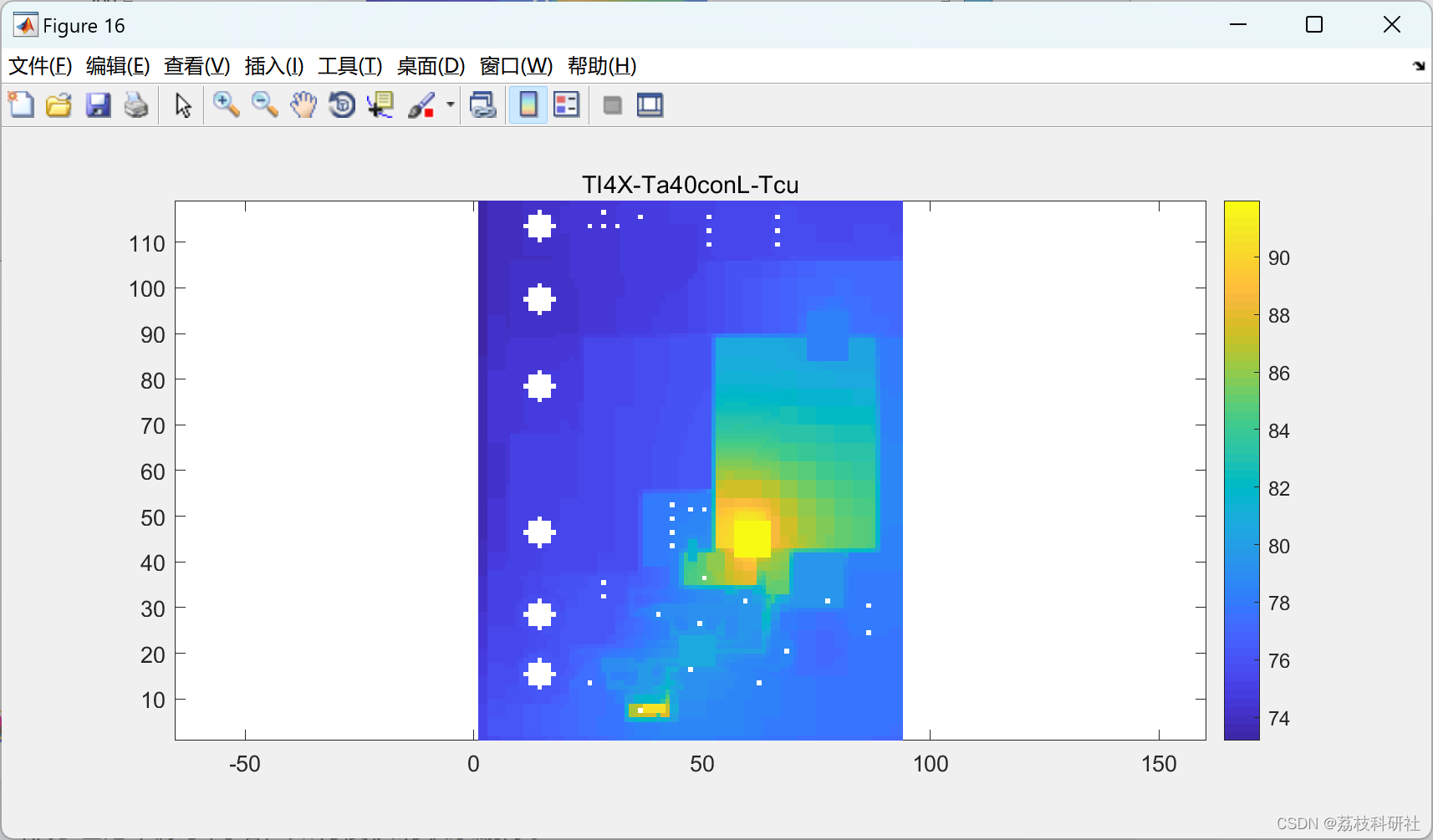
3. 结果分析

温度分布：最高温度出现在MOSFET下方，达98°C（传统模型预测为110°C），辐射散热贡献约8%。
功耗迭代：根据温升反推元件功耗，进行二次修正，误差<5%。

四、技术优势与挑战

1. 优势

精度提升：辐射传热和元件热阻的动态耦合使温度预测更贴近实测。
效率突破：多重网格策略使复杂PCB模型求解时间缩短50%以上。
扩展性：方法可推广至AC/DC转换器、高密度IC封装等领域。

2. 挑战

元件热参数依赖：需厂商提供精确的RthRth和功耗-温度曲线。
辐射模型简化：S2S模型假设表面灰体且介质透明，不适用于半透明材料或光学厚介质。

五、未来方向

多物理场耦合：集成电磁-热-结构耦合分析，优化高频开关下的热应力。
AI加速建模：利用神经网络预测热阻参数和辐射角系数，减少迭代次数。
标准化接口：推动ECAD工具与热仿真软件数据互通，实现设计-仿真闭环。

📚2 运行结果

部分代码：

% The radiation boudary condition is considered in the coupling method by
% using the radiation-equivalent HTC.
% The equivalent radiation power is also composed of three parts,
% including the part from the components,the part from the top metal layer,
% and the part from the insulating region of the top side.
function [qH21,qHM,qHI,qHall]=RadiationbyHTC(Sc,Tc,Hc,dc2,TMu,TIu,HR,HRINS,LF16,LF4,LPRP,PFMAP,LINS16,LINS4,LINS)

% The part from the components was denoted by the array of qH21:
qH21=Tc.*Sc.*Hc;

% The part from the top metal layer was denoted by the array of qHM:
TMu(1:LF16)=TMu(1:LF16)*16*dc2;
TMu(LF16+1:LF16+LF4)=TMu(LF16+1:LF16+LF4)*4*dc2;
TMu(LF16+LF4+1:LPRP)=TMu(LF16+LF4+1:LPRP)*dc2;
% TMu(LPRP+1:LALL)=0;
QRONE=TMu(LF16+LF4+1:LPRP);
QRONE(PFMAP)=0;
TMu(LF16+LF4+1:LPRP)=QRONE;
qHM=sum(TMu.*HR);

% The part from the insulating region was denoted by the array of qHI:
TIu(1:LINS16)=TIu(1:LINS16)*16*dc2;
TIu(LINS16+1:LINS16+LINS4)=TIu(LINS16+1:LINS16+LINS4)*4*dc2;
TIu(LINS16+LINS4+1:LINS)=TIu(LINS16+LINS4+1:LINS)*dc2;
qHI=sum(TIu(1:LINS).*HRINS);

% The total radiation power was calculated as follows:
qHall=qHM+qHI+sum(qH21);