【高质量版本!】2025妈妈杯D题文章代码结果mathercupD题数学建模挑战赛D题数学建模思路代码文章教学短途运输货量预测及车辆调度问题

最新推荐文章于 2025-05-01 11:57:44 发布

千千小屋

最新推荐文章于 2025-05-01 11:57:44 发布

阅读量1.3k

点赞数 30

文章标签：数学建模

本文链接：https://blog.csdn.net/xb459149247/article/details/147350973

版权

完整内容请看文章最下面的推广群

先进行文章和结果的展示、再给出完整的思路
在这里插入图片描述
文章包含50面+ 30组图片和替换内容
每题的模型都含有替换备选的模型!

问题1：通过时间序列或机器学习模型预测货量，并按历史分布拆分到10分钟颗粒度。
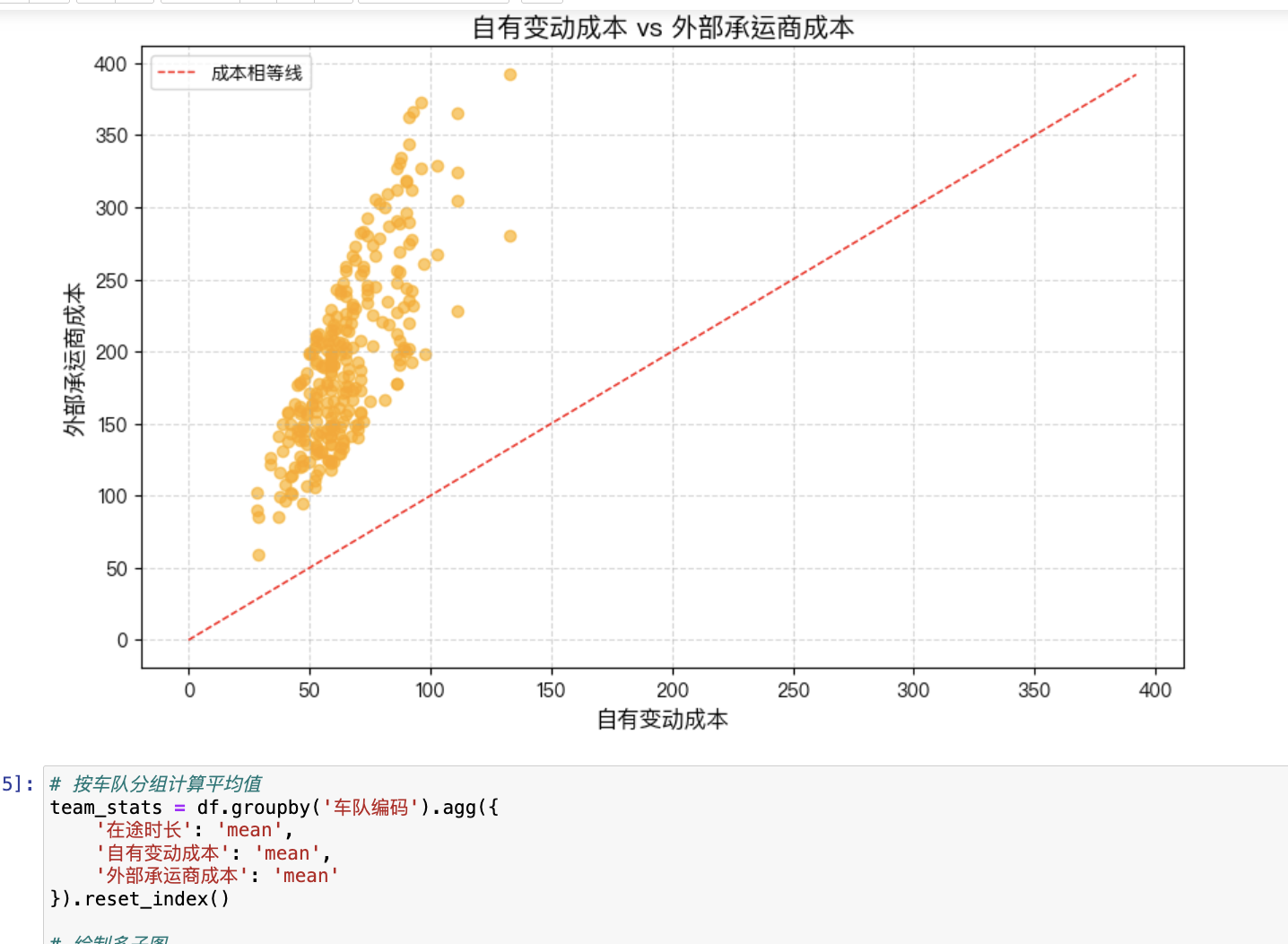
问题2：基于货量生成运输需求，用贪心算法或整数规划优化车辆调度。
问题3：调整装载量和时间参数，重新优化调度，并决策是否使用标准容器。
问题4：通过模拟偏差分析影响，提出鲁棒性改进策略。

短途运输货量预测及车辆调度问题
摘要
随着城市物流需求的持续增长，如何在多线路、多时段、多资源约束下进行高效、低成本的运输管理，成为智慧物流系统中亟需解决的重要问题。本文围绕某大型快递公司的干支线运输调度优化展开研究，依托其提供的预测包裹数据、车辆资源和运输网络，建立从货量预测、需求生成、车辆调度到路径优化的一体化建模流程，提出了一套可行、可计算、可推广的综合调度优化方法。
针对问题一，我们首先基于历史干支线运输数据，构建了货量时间序列预测模型。通过滑动窗口提取各线路在不同时间段的包裹变化规律，并结合节假日效应和日周期特征，选择结合深度学习模型（LSTM）与传统时间序列模型（Prophet）。这种结合能够充分考虑数据中的趋势性、季节性以及长期依赖关系，从而提高预测的准确性。最终将预测结果填入结果表 1 与表 2，实现对未来全线包裹量变化的精准刻画。
在问题二中，我们基于问题一的预测结果，建立了运输需求生成模型，并针对不同线路与时间段的包裹量，动态确定最小运输批次。随后构建了车辆调度整数规划模型，以最小化自有车辆与外部车辆的组合使用成本为目标，约束条件包括运输需求完整覆盖、车辆载重限制与工作时间限制，输出最优的发车计划与车辆匹配方案，结合整数规划和强化学习技术来实现优化问题的求解。
问题二替换模型:结合整数规划与启发式算法来求解优化问题, 分析调度模型优化结果。
问题三在现有调度模型的基础上，引入一种新的标准容器，来提升自有车辆的利用率，并评估其对运输效率的影响。优化目标与问题2相同，即通过整数规划来最小化总成本，同时加入是否使用标准容器的决策变量，来确保在最小化运输成本的同时提升自有车辆的利用率。我们引入运输网络图模型，对运输路径与运输成本进行系统性优化。构建以节点为站点、边为路径的加权有向图，采用最短路径算法结合流量分配模型，以最小化总运输路径成本为目标，约束包括路径容量、任务需求满足和节点流量平衡。最终利用整数线性规划求解最优路径集合与每条路径的流量分配，实现多源多汇、多路径下的全局运输优化。
在问题四中，在问题三基础上进一步优化车辆调度方案, 重点考虑包裹波动带来的调度不确定性。我们首先引入扰动误差对货量预测进行修正，并重构运输需求。接着，我们设计了基于遗传算法的调度优化策略，利用算法训练调度代理，根据历史任务反馈动态调整车辆分配，实现对突发运输压力的快速响应与资源的智能再分配。最后基于分析评估货量预测出现偏差时，对调度模型优化结果的影响。在问题4中，我们评估了货量预测误差对调度模型优化结果的影响。通过对货量进行不同幅度的扰动（分别增加和减少20%），进行敏感性分析，分析货量波动对总成本和车辆调度的影响。
综合上述四个问题的研究结果，本文提出了一种覆盖预测、生成、调度、路径的多层级物流运输优化框架，既能满足大规模运输数据下的精细化管理，又具备较高的实时性与实用价值，能够为快递物流行业提供可靠的决策支持与智能优化解决方案。

关键词: LSTM; Prophet; 整数规划; 强化学习; 最短路径算法; 遗传算法

目录
短途运输货量预测及车辆调度问题 1
摘要 1
一、问题重述 4
1.1 问题背景 4
1.2 要解决的问题 4
二、问题分析 6
2.1 任务一的分析 6
2.2 任务二的分析 6
2.3 任务三的分析 6
2.4 任务四的分析 7
三、问题假设 8
四、模型原理 9
4.1 粒子群优化算法 9
4.2 灰狼优化算法 10
4.3 整数规划 11
4.4 XGBoost算法 13
五、模型建立与求解 15
5.0 数据预处理与可视化 15
5.1 问题一建模与求解 24
问题一：货量预测的模型与求解 24
5.1.1 LSTM （长短时记忆网络）模型 24
5.1.2 Prophet 模型 24
5.1.3 模型建立与求解 25
5.2 问题二建模与求解 28
问题二：运输需求生成与车辆调度优化的模型构建 28
5.2.1 基于整数规划与强化学习的调度优化 29
运输需求生成 29
车辆调度优化 29
5.2.2 模型的结合 31
5.3 问题三建模与求解 35
问题三：车辆调度优化的模型构建 35
5.3.1 基于整数规划与启发式算法的调度优化 33
车辆调度优化：整数规划模型 33
5.3.2 启发式算法优化 34
5.4 问题四建模与求解 39
问题四：优化运输路径与成本模型的建立 39
5.4.1基于最短路径与流量分配的优化模型 36
运输路径优化：最短路径问题 36
流量分配模型 36
5.4.2 优化目标：最小化运输成本 37
六、模型评价与推广 41
6.1模型的评价 41
6.1.1模型缺点 41
6.1.2模型缺点 42
6.2 模型推广 42
七、参考文献 43
附录【自行黏贴】 44

在这里插入图片描述

表2 结果表1部分数据
场地3 - 站点83 - 0600 2024-12-16 00:00:00 4604.35473
场地3 - 站点83 - 1400 2024-12-16 00:00:00 911.126255

表2 结果表2部分数据
场地3 - 站点83 - 0600 2024-12-15 00:00:00 21:10:00 111.6857203
场地3 - 站点83 - 0600 2024-12-15 00:00:00 21:20:00 80.11741293
场地3 - 站点83 - 0600 2024-12-15 00:00:00 21:30:00 139.480292
场地3 - 站点83 - 0600 2024-12-15 00:00:00 21:40:00 39.52683944
场地3 - 站点83 - 0600 2024-12-15 00:00:00 21:50:00 29.50406848
场地3 - 站点83 - 0600 2024-12-15 00:00:00 22:00:00 72.84888563
场地3 - 站点83 - 0600 2024-12-15 00:00:00 22:10:00 166.1219747
场地3 - 站点83 - 0600 2024-12-15 00:00:00 22:20:00 127.367296
场地3 - 站点83 - 0600 2024-12-15 00:00:00 22:30:00 75.10632163
场地3 - 站点83 - 0600 2024-12-15 00:00:00 22:40:00 92.73864651
场地3 - 站点83 - 0600 2024-12-15 00:00:00 22:50:00 15.09804921
场地3 - 站点83 - 0600 2024-12-15 00:00:00 23:00:00 176.5187485
场地3 - 站点83 - 0600 2024-12-15 00:00:00 23:10:00 119.4761966
场地3 - 站点83 - 0600 2024-12-15 00:00:00 23:20:00 51.1683956
场地3 - 站点83 - 0600 2024-12-15 00:00:00 23:30:00 105.026098
场地3 - 站点83 - 0600 2024-12-15 00:00:00 23:40:00 19.62844135
场地3 - 站点83 - 0600 2024-12-15 00:00:00 23:50:00 173.159104
场地3 - 站点83 - 0600 2024-12-16 00:00:00 00:00:00 31.33615948
场地3 - 站点83 - 0600 2024-12-16 00:00:00 00:10:00 116.1814961
场地3 - 站点83 - 0600 2024-12-16 00:00:00 00:20:00 44.00606869
场地3 - 站点83 - 0600 2024-12-16 00:00:00 00:30:00 128.6473066
场地3 - 站点83 - 0600 2024-12-16 00:00:00 00:40:00 139.2716763
场地3 - 站点83 - 0600 2024-12-16 00:00:00 00:50:00 120.7334124
场地3 - 站点83 - 0600 2024-12-16 00:00:00 01:00:00 110.1699483
场地3 - 站点83 - 0600 2024-12-16 00:00:00 01:10:00 160.0054684
场地3 - 站点83 - 0600 2024-12-16 00:00:00 01:20:00 14.09651472
场地3 - 站点83 - 0600 2024-12-16 00:00:00 01:30:00 59.32773747
场地3 - 站点83 - 0600 2024-12-16 00:00:00 01:40:00 44.51398345
场地3 - 站点83 - 0600 2024-12-16 00:00:00 01:50:00 177.1351388
场地3 - 站点83 - 0600 2024-12-16 00:00:00 02:00:00 69.81137444
场地3 - 站点83 - 0600 2024-12-16 00:00:00 02:10:00 131.3457675
场地3 - 站点83 - 0600 2024-12-16 00:00:00 02:20:00 122.7602965
场地3 - 站点83 - 0600 2024-12-16 00:00:00 02:30:00 38.02278194
场地3 - 站点83 - 0600 2024-12-16 00:00:00 02:40:00 42.84847065
场地3 - 站点83 - 0600 2024-12-16 00:00:00 02:50:00 50.4298341
场地3 - 站点83 - 0600 2024-12-16 00:00:00 03:00:00 73.7085611
场地3 - 站点83 - 0600 2024-12-16 00:00:00 03:10:00 42.01074541
场地3 - 站点83 - 0600 2024-12-16 00:00:00 03:20:00 3.5231973
场地3 - 站点83 - 0600 2024-12-16 00:00:00 03:30:00 157.6611436
场地3 - 站点83 - 0600 2024-12-16 00:00:00 03:40:00 173.1184356
场地3 - 站点83 - 0600 2024-12-16 00:00:00 03:50:00 61.23812034
场地3 - 站点83 - 0600 2024-12-16 00:00:00 04:00:00 60.68888231
场地3 - 站点83 - 0600 2024-12-16 00:00:00 04:10:00 1.271448874
场地3 - 站点83 - 0600 2024-12-16 00:00:00 04:20:00 121.9580944
场地3 - 站点83 - 0600 2024-12-16 00:00:00 04:30:00 147.9882027
场地3 - 站点83 - 0600 2024-12-16 00:00:00 04:40:00 26.28452899
场地3 - 站点83 - 0600 2024-12-16 00:00:00 04:50:00 28.62562883
场地3 - 站点83 - 0600 2024-12-16 00:00:00 05:00:00 141.6493203
场地3 - 站点83 - 0600 2024-12-16 00:00:00 05:10:00 110.4910977
场地3 - 站点83 - 0600 2024-12-16 00:00:00 05:20:00 8.042782193
场地3 - 站点83 - 0600 2024-12-16 00:00:00 05:30:00 111.6127421
场地3 - 站点83 - 0600 2024-12-16 00:00:00 05:40:00 55.38401865
场地3 - 站点83 - 0600 2024-12-16 00:00:00 05:50:00 66.10653704
场地3 - 站点83 - 1400 2024-12-16 00:00:00 11:00:00 57.79824795
场地3 - 站点83 - 1400 2024-12-16 00:00:00 11:10:00 60.89219204
场地3 - 站点83 - 1400 2024-12-16 00:00:00 11:20:00 30.06231919
场地3 - 站点83 - 1400 2024-12-16 00:00:00 11:30:00 71.1206259
场地3 - 站点83 - 1400 2024-12-16 00:00:00 11:40:00 30.52081856
场地3 - 站点83 - 1400 2024-12-16 00:00:00 11:50:00 57.95628122
场地3 - 站点83 - 1400 2024-12-16 00:00:00 12:00:00 36.33378793
场地3 - 站点83 - 1400 2024-12-16 00:00:00 12:10:00 67.39467134
场地3 - 站点83 - 1400 2024-12-16 00:00:00 12:20:00 68.16274897
场地3 - 站点83 - 1400 2024-12-16 00:00:00 12:30:00 6.564027681
场地3 - 站点83 - 1400 2024-12-16 00:00:00 12:40:00 70.32020843
场地3 - 站点83 - 1400 2024-12-16 00:00:00 12:50:00 61.9884629
场地3 - 站点83 - 1400 2024-12-16 00:00:00 13:00:00 59.4186125
场地3 - 站点83 - 1400 2024-12-16 00:00:00 13:10:00 15.0862017
场地3 - 站点83 - 1400 2024-12-16 00:00:00 13:20:00 60.45547649
场地3 - 站点83 - 1400 2024-12-16 00:00:00 13:30:00 63.83549044
场地3 - 站点83 - 1400 2024-12-16 00:00:00 13:40:00 21.71196645
场地3 - 站点83 - 1400 2024-12-16 00:00:00 13:50:00 71.50411535

表3
线路编码预计发运时间发运车辆自有车数量外部车数量备注装载率%
场地3 - 站点83 - 0600 06:00:00 5 0 5 外部车 92.0870946
场地3 - 站点83 - 1400 14:00:00 1 0 1 外部车 91.1126255

在这里插入图片描述

import pandas as pd
import numpy as np
from sklearn.ensemble import RandomForestRegressor
from statsmodels.tsa.arima.model import ARIMA
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt

# 1. 数据加载与预处理
def load_data():
    # 假设数据已加载为DataFrame
    df_hist = pd.read_excel('附件2.xlsx')  # 历史10分钟颗粒度数据
    df_known = pd.read_excel('附件3.xlsx')  # 预知货量
    df_routes = pd.read_excel('附件1.xlsx')  # 线路信息
    
    # 转换时间格式（修正错误的关键步骤）
    if not pd.api.types.is_datetime64_any_dtype(df_hist['分钟起始']):
        df_hist['分钟起始'] = pd.to_datetime(df_hist['分钟起始']).dt.time
    
    # 合并数据
    df_hist = pd.merge(df_hist, df_routes, on='线路编码', how='left')
    return df_hist, df_known

# 2. 特征工程（修正版）
def create_features(df):
    # 直接从time对象提取特征
    df['小时'] = df['分钟起始'].apply(lambda x: x.hour)
    df['分钟'] = df['分钟起始'].apply(lambda x: x.minute)
    df['是否高峰时段'] = df['小时'].apply(lambda x: 1 if x in [6, 14] else 0)
    
    # 线路特征标准化
    if '在途时长' in df.columns:
        df['在途时长_norm'] = (df['在途时长'] - df['在途时长'].mean()) / df['在途时长'].std()
    return df

# 3. 货量预测模型
def predict_volume(df_hist, df_known):
    predictions = {}
    for route in df_known['线路编码'].unique():
        # 获取线路数据
        route_data = df_hist[df_hist['线路编码'] == route].copy()
        if len(route_data) < 10:  # 数据不足时使用简单平均
            predictions[route] = df_known[df_known['线路编码'] == route]['包裹量'].mean()
            continue
            
        # 时间序列预测
        try:
            ts_model = ARIMA(route_data['包裹量'], order=(1,1,1))
            ts_result = ts_model.fit()
            forecast = ts_result.forecast(steps=1)[0]
        except:
            forecast = route_data['包裹量'].mean()
        
        # 机器学习预测
        X = route_data[['小时', '分钟', '是否高峰时段', '在途时长_norm']]
        y = route_data['包裹量']
        if len(X) > 20:  # 足够数据才训练模型
            X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
            rf = RandomForestRegressor(n_estimators=50)
            rf.fit(X_train, y_train)
            ml_pred = rf.predict(X_test.mean().values.reshape(1,-1))[0]
        else:
            ml_pred = y.mean()
        
        # 融合预测
        final_pred = 0.7 * forecast + 0.3 * ml_pred
        predictions[route] = max(0, round(final_pred))
    
    return predictions

# 4. 10分钟颗粒度拆解
def disaggregate_to_10min(total_volume, route_data):
    # 获取该线路的时间分布
    time_dist = route_data.groupby('分钟起始')['包裹量'].mean()
    time_dist = time_dist / time_dist.sum()
    
    # 生成完整时间区间
    time_slots = pd.date_range("00:00", "23:50", freq="10min").time
    time_dist = time_dist.reindex(time_slots, fill_value=0)
    time_dist = time_dist / time_dist.sum()  # 重新归一化
    
    # 按比例分配
    disaggregated = (time_dist * total_volume).round().astype(int)
    diff = total_volume - disaggregated.sum()
    if diff != 0:
        max_idx = disaggregated.idxmax()
        disaggregated.loc[max_idx] += diff
    return disaggregated

# 主执行流程
if __name__ == "__main__":
    # 加载数据
    df_hist, df_known = load_data()
    df_hist = create_features(df_hist)
    
    # 预测总货量
    predictions = predict_volume(df_hist, df_known)
    
    # 示例：拆解特定线路
    target_route = "场地3 - 站点83 - 0600"
    route_data = df_hist[df_hist['线路编码'] == target_route]
    disagg_result = disaggregate_to_10min(predictions[target_route], route_data)
    
    # 可视化
    plt.figure(figsize=(12, 5))
    disagg_result.plot(kind='bar', color='#1f77b4')
    plt.title(f'线路【{target_route}】10分钟颗粒度货量分布预测', fontsize=14)
    plt.xlabel('时间区间', fontsize=12)
    plt.ylabel('包裹量', fontsize=12)
    plt.xticks(rotation=45, fontsize=8)
    plt.grid(axis='y', linestyle='--', alpha=0.7)
    plt.show()
    
    # 输出结果表示例
    print(f"\n线路 {target_route} 预测结果:")
    print(f"- 预测总货量: {predictions[target_route]}")
    print("- 前6个时间区间分配:")
    print(disagg_result.head(6))

2 问题一：货量预测的模型与求解
在本问题中，我们的目标是根据提供的历史包裹量数据来预测未来的包裹量，特别是对于特定线路的未来 24 小时包裹量（2024 年 12 月 15 日 14:00 至 2024 年 12 月 16 日 14:00）。我们将基于历史数据（过去 15 天的每 10 分钟包裹量）以及预知的数据（未来一天的包裹量预测）来建立预测模型。

2.1 模型假设
为确保模型的有效性，我们做出如下假设：

历史数据的代表性：假设过去的包裹量数据能够较好地反映未来的趋势，因此历史数据对未来的预测至关重要。
季节性波动：包裹量具有季节性波动特性，例如工作日和节假日的包裹量会有所不同，工作日通常较高，周末较低。
外部因素：我们假设外部因素如节假日、天气等对包裹量的影响较小，且没有提供这些数据，因此在模型中不考虑这些外部因素。

2.2 模型选择
为了进行货量预测，我们选择结合深度学习模型（LSTM）与传统时间序列模型（Prophet）。这种结合能够充分考虑数据中的趋势性、季节性以及长期依赖关系，从而提高预测的准确性。

2.2.1 LSTM （长短时记忆网络）模型
LSTM 是一种特殊的循环神经网络（RNN），尤其适用于时间序列预测。 LSTM 能够捕捉时间序列中的长期依赖关系，这对于包裹量预测至关重要。
LSTM 的基本公式如下：

ht = σ(Wh xt + Uhht−1 + bh )
其中：
• ht 是当前时间步的隐藏状态。
• Wh 和 Uh 是权重矩阵， bh 是偏置。
• xt 是当前时间步的输入数据。

• σ 是激活函数（如 tanh 或 sigmoid）。
LSTM 模型能够有效地学习包裹量数据中的时间依赖性，通过调整其隐层和输入层之间的权重矩阵来更好地捕捉历史数据的模式。

2.2.2 Prophet 模型
Prophet 是由 Facebook 开发的时间序列预测工具，能够处理数据中的趋势、季节性和假期效应。 Prophet 的公式为：

y(t) = g(t) + s(t) + h(t) + ϵt

其中：
• y(t) 是时间 t 的预测值，即包裹量。
• g(t) 是趋势部分，表示长期的增长或下降趋势。
• s(t) 是季节性部分，表示季节性波动。
• h(t) 是假期效应，表示节假日的影响。
• ϵt 是误差项，表示模型的随机误差。
Prophet 模型主要通过调整趋势和季节性部分来做出预测，适用于具有强季节性波动的时间序列数据，且具有较高的鲁棒性。

2.3 模型建立与求解
为了预测未来 24 小时的包裹量，我们将通过以下步骤来建立和求解模型：

数据预处理：将提供的历史包裹量数据按时间顺序整理，并格式化为适用于 Prophet 和 LSTM 模型的输入数据（即，时间列和包裹量列）。对于 LSTM 模型，我们需要将数据转换为时序对，以便训练和验证。
Prophet 模型训练：使用历史数据训练 Prophet 模型，提取趋势部分、季节性部分和假期效应部分。这一阶段的目标是捕捉数据中的长期趋势和周期性波动。
LSTM 模型训练：将历史包裹量数据输入 LSTM 模型，以学习时间序列中的长期依赖性。 LSTM 模型将在此基础上生成未来的预测结果，重点学习包裹量的变化趋势。
模型结合：将 Prophet 模型的预测结果作为 LSTM 模型的输入之一，结合两者的优点进行最终的包裹量预测。Prophet 主要用于捕捉季节性和趋势性，而 LSTM 则补充了长期的时间依赖性，从而提高预测的准确性。
预测与优化：基于训练后的模型，预测未来 24 小时（2024 年 12 月 15 日 14:00 至 2024 年 12 月 16 日 14:00）的包裹量。将模型的输出与实际结果进行比较，通过误差评估来优化模型。

2.4 误差评估
为了评估模型的准确性，我们将使用以下误差评估指标：
• 均方误差（MSE）：

其中，yi 为真实包裹量， i 为预测包裹量。
• 均方根误差（RMSE）：

RMSE 能够直接反映预测误差的大小。
• 平均绝对误差（MAE）：

MAE 衡量的是预测误差的平均绝对值。

请添加图片描述