自动驾驶规划术语与搜索空间的几种方法

1. 导读

目前，自动驾驶或自动驾驶汽车是学术界和汽车界研究的核心，因为它具有多方面的优势，包括提高安全性、减少拥堵、降低排放和提高机动性。其实软件是支持自动驾驶的关键驱动因素，在将乘客或货物从指定的起点运送到指定的目的地时，其中负责关键任务决策的规划算法是核心中的核心。本文将从自动驾驶规划的相关术语开始介绍，之后将会介绍几种搜索空间的方法，至于基于前者的规划技术将在今后推出。

2. 相关术语

本节描述了机器人规划领域文献中常用的关键概念术语，因此也介绍了自动驾驶车辆。如前所述，本文侧重于局部道路层面的规划，而非全球层面的规划（即GPS导航路线规划）。

根据固定坐标系唯一定义车辆位置和方向的独立属性集称为配置向量 (Eskandarian, 2012)。因此，车辆所有配置的集合构成了配置空间。

描述自动驾驶车辆在某一时刻和某一特定地点的状态的一组属性值被称为该时刻车辆的“状态” (Eskandarian, 2012)。最常见的属性集，定义为向量，用于表示车辆的状态是位置 (x, y, z)，方向 (hx, hy, hz)，线速度 (vx, vy, vz) 和角速度 (xx, xy, xz)。随后，状态空间表示车辆可能处于的所有可能状态的集合。在下一节中将看到，状态空间的数学表示不同于车辆规划所采用的方法。对于每一个规划问题，都应该考虑显式表示和算法效率之间的权衡。可用于构造配置或状态空间的表示将在第2.2节中讨论。

单车模型是一个车辆的动力学/运动学模型，其中两个前轮和两个后轮分别被一个前轮和一个后轮代替。车辆在平面上移动，其坐标由向量（x, y, ψ）描述，其中x，y是重心位置，ψ是车辆的方向。车辆重心处的速度表示为V，方向盘的角度用前轮角表示。并与车辆纵轴成一个角度。这个角度被称为车辆的侧滑角β(单车模型的一个基本假设是内滑角、外滑角和转向角相等)。

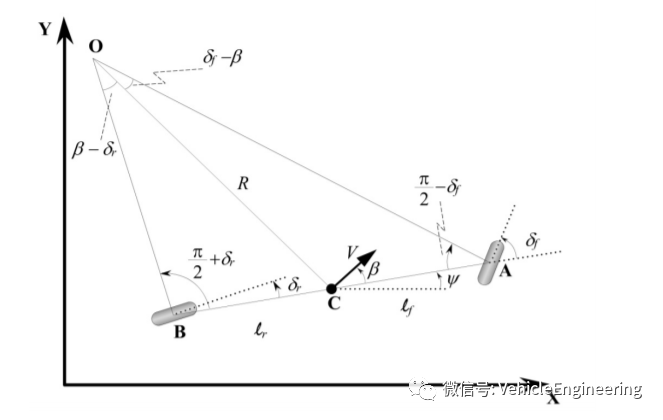
如果可控自由度等于总自由度，则机器人是完整自由度的（holonomic），如果可控制的自由度小于总自由度，则称为非完整约束的（non-holonomic）。汽车具有三个自由度（也有说四个2个笛卡尔坐标）；即它在地图两个轴上的位置及其方向。但是，只有两个可控制的自由度，即加速度（或制动）和方向盘转向角。这使驾驶员很难向任何方向转动汽车（除非汽车打滑或滑行）。

行为输入（actions）是导致车辆状态变化的系统输入（如加速度、转向角）。行为输入（actions）要么被定义为时间的函数，要么被定义为状态和时间的函数。行为操作空间（Action space）表示可应用于状态空间的所有可能操作的集合。

给定一个配置空间（configuration space）或一个状态空间（state space），规划是一个计算密集型任务，要求高内存利用率。在机器人运动领域（包括公路和越野车辆和物体），规划是在不同的层次上进行的。最高级别的规划涉及到从起点到终点的路线规划，工作空间基本上仅限于表示底层道路网络的数字地图。最低级的规划是根据车辆动力学规划出一条平滑的轨迹，这种规划是在高维状态的小（局部）搜索空间中制定的。为了便于描述和讨论，本文其余部分定义了以下术语

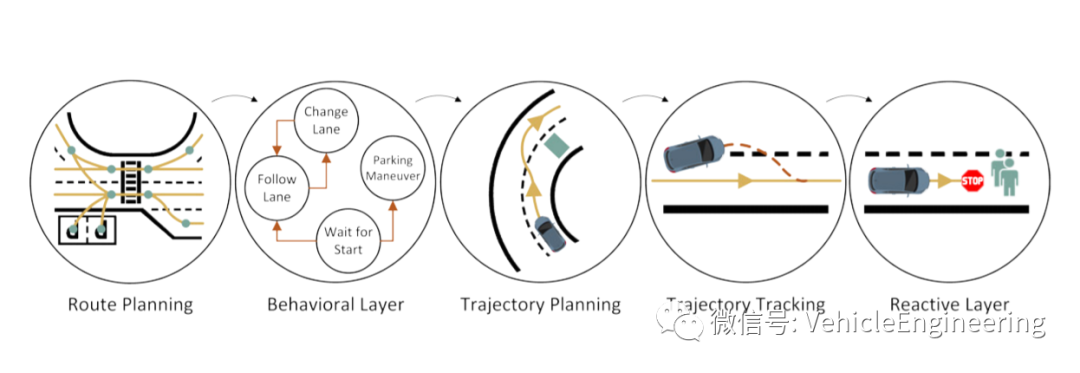
路径表示为以边界配置开始和结束的连续配置序列，即初始配置和终止配置（Eskandarian，2012）。换言之，路径是车辆为了到达目的地而不与障碍物相撞而应遵循的几何轨迹。

路径规划是寻找从初始配置到给定终止配置的几何路径的问题，使得路径上的每个配置和状态（如果考虑时间）都是可行的。可行的配置/状态不会导致碰撞，并遵循一组运动约束，例如道路和车道边界以及交通规则。值得注意的是，在讨论路径规划的整篇论文中，在上述约束条件下，寻找最佳和最安全的几何轨迹是非常重要的，这些约束条件也有关于交通规则的逻辑论证。

操纵是关于车辆在道路上的位置和速度的车辆运动的高级特征。操纵的例子包括“直行”、“转弯”、“超车”等。如果根据交通规则或其他规则安全地进行了操纵，则该操纵属于名义操纵。

操纵规划解决的问题是，在考虑路径规划中指定的路径的同时，为车辆做出最佳的高层决策。

轨迹被表示为车辆访问的一系列状态，由时间和速度参数化。轨迹规划（又称轨迹生成）是指在满足车辆动力学特性的基础上，受导航舒适性、2车道边界和交通规则约束，在避免的同时，实时规划实际车辆从一个可行状态过渡到下一个可行状态的过程时间、障碍物，包括其他道路使用者以及地面粗糙度和沟渠。

轨迹规划由时间、加速度或速度参数化，通常称为运动规划。在每个规划周期中，路径规划器模块根据车辆车载传感器的速度和视线，从车辆的当前位置生成多个具有前瞻距离的轨迹，并根据某些成本函数评估每个轨迹，以确定最佳轨迹。

轨迹规划是按固定的时间间隔安排的；其长度在很大程度上取决于接收新传感器数据的频率。例如，在VisLab洲际自主挑战赛（VisLab Intercontinental Autonomic Challenge）期间测试的控制器中，每隔100毫秒（ms）安排一次轨迹规划（Broggi等人，2012年）。监控当前车辆位置和确定轨迹之间的误差；当检测到超过预定义阈值的误差时，触发轨迹修正计划。应当指出的是，在空中交通管制的背景下，有大量关于飞机飞行轨迹规划的文献。然而，飞机的轨迹规划与公路车辆的轨迹规划有很大的不同。飞机的运行环境和分配的空间不同于人口过多、多式联运、拥挤的道路网络，后者也受到道路几何结构、车道和大量未出现在空中的障碍物的制约。此外，飞机的自由度、动力学和尺寸与公路车辆不同，车辆和飞机的轨迹规划（必须考虑所有这些参数）需要不同的方法。例如，如chuster（2015）所述，飞机的轨迹是4D（包括空间坐标 (x, y, z) 和时间，而道路车辆主要作用于2D空间或3D空间（如果加上时间）。此外，飞机运动规划的状态向量包括三维位置坐标（x、y和高度）、风速和飞机质量。然而，道路车辆的状态向量不考虑空气速度和车辆质量。因此，可以理解为飞机的轨迹被处理为6个自由度，而公路车辆的轨迹通常只处理3个自由度。

大多数现有的轨迹规划算法的实现遵循两个步骤：

（i）第一步在低分辨率/低维搜索空间生成轨迹；

（ii）在第二步中，在更高分辨率/高维搜索空间上平滑得到的最优轨迹。规划模块是实现车辆完全自动驾驶的一个组成部分，轨迹规划器的输出输入到车辆控制模块的低级转向/操纵控制单元。

3. 搜索空间的方法

规划自动驾驶车辆在道路上的行程时，需要以能够查询路径的方式来表示环境。这意味着必须将物理空间转换为配置或状态空间。当车辆在道路上行驶时，传感器的数据和从高精地图中获得的信息被用于将环境的连续性转换为道路网络的数字表示，这是就是自动驾驶规划的基本空间。

这种离散化的自动驾驶空间搜寻必须在效率、密度和表现力方面得到有效处理，因为高密度网络可能导致高计算成本和高功率。虽然不充分的空间表示虽然可以提高计算速度，但可能会导致自动驾驶空间里面不准确，那么就会有碰撞安全风险，所以空间搜寻是自动驾驶非常重要的一步。

当然空间搜寻方法有仅仅使用道路边界和障碍物的位置在连续坐标系中启动搜索，例如，Driving Corridors。有分解（或镶嵌）技术以更高的分辨率分析空间，包括Voronoi Diagram，occupancy grids，cost maps，lattices。本节将大概介绍以上几种方法。

3.1. Voronoi Diagram

Voronoi图描述了彼此接近的点，或他们的最近的邻居之间的空间关系。它是从点或位置派生的一组连接面。Voronoi“区域”的每一条线都位于两点之间。

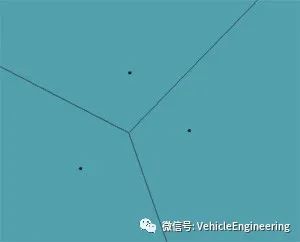
在这里，您可以看到每条线恰好位于两点之间的中间，并且它们都在中间汇合。让我们向场景中添加更多点，看看会发生什么：

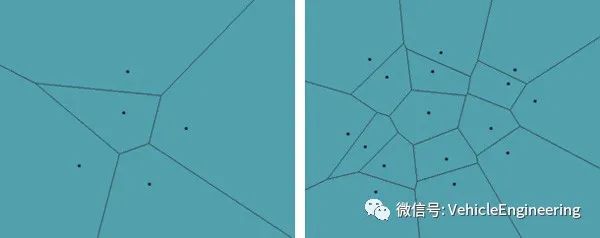
现在，这变得越来越有趣！我们开始获取实际区域，那么每个地区告诉我们什么？我们知道，在区域内时，我们保证最接近也在该区域内的单点。这告诉我们很多有关我们附近的东西的信息，这是Voronoi图中基本的空间关系。

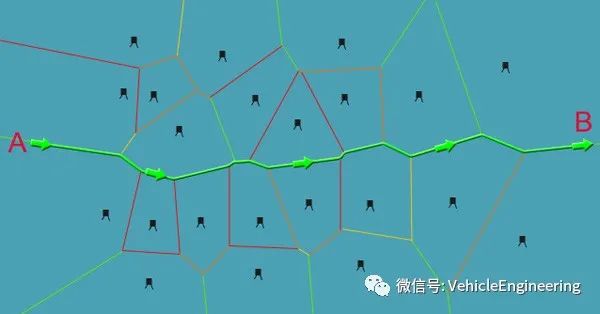
通过这种空间关系我们就可以找出从A到B的路径，当然你可以赋予不同的权重可以寻找最快和最安全的路径。

Voronoi Digrams生成使车辆和周围障碍物之间的距离最大化的路径。用于搜索Voronoi图的算法是完整的，如果自由空间中存在路径，它也会出现在Voronoi Digrams 如图a所示，灰线代表Voronoi边缘（即与检测到的障碍物有最大距离的边缘），并产生一个车辆可以执行其行程的空间。2010年Dolgov等人通过将Voronoi Digrams与潜在的场景相结合，将Voronoi Digrams用于停车场中自动驾驶路径规划；这是一种源自移动机器人技术的避障算法。这种被称为Voronoi digrams的组合方法是为了克服传统的势场方法在狭窄通道（产生高潜在性）中的问题而开发的，这种方法使这些通道实际上不可穿越。Voronoi图通常用于静态环境中的规划，例如停车场。此外，Voronoi digrams本身并不适用于道路路径规划，因为车辆沿其行驶的Voronoi边可能是不连续的，不适合非完整约束车辆。

3.2. Occupancy Grid & Cost maps

占用网格和成本图以类似的方式工作；它们都将状态空间离散成一个网格，并且网格的每个单元都与单元被障碍物占用的概率相关，或者与穿越的可行性或风险成比例的成本相关。风险或可行性主要通过考虑障碍物、车道和道路边界的存在来计算。基于网格的方法可以快速找到计算能力较低的解决方案，但难以以稳健的方式解释非线性动力学，并且在存在障碍物的情况下。如图1b和c所示，占用网格由一个网格组成，其中包含障碍物的位置和（有时）显示其预期运动的附加速度；而在成本图中，某个单元的成本越高，其在地图上的表现就越强烈。

3.3. State Lattice

状态格可以看作是网格的泛化。正如grids是通过重复矩形或正方形来离散连续空间一样，lattices是通过有规律地重复原始路径来构建的，这些路径连接了车辆的可能状态，如图1d所示。然后规划问题就减少到了一个边界值将原始状态与所需最终状态相连接的问题。状态格克服了基于grids的技术在效率上的局限性，而不增加计算能力。

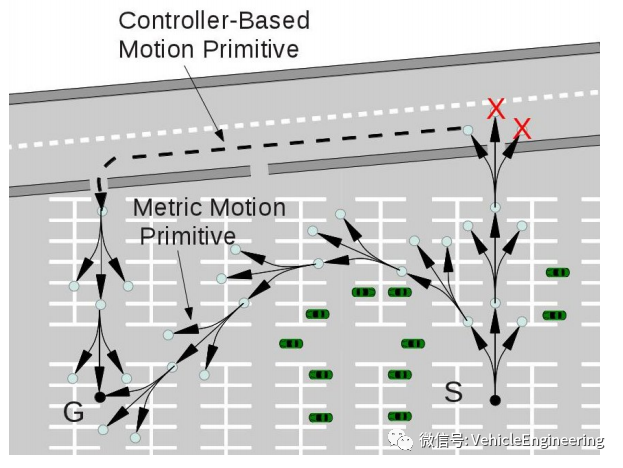
3.4. Driving Corridors

Driving Corridors代表一个连续的无碰撞空间，以道路和车道边界以及其他障碍物为边界，车辆将在此处移动。驾驶走廊基于详细数字地图（高精地图）上给出的车道边界信息，或使用同步定位和制图（SLAM）技术构建的地图。车道边界形成了驾驶走廊的外部边界，在存在障碍物时受到限制。在图1e中，根据选择的操纵为每辆车建造一个驾驶走廊。确定走廊的中心线形成了一条路径，在该路径上，自动驾驶车辆将沿着该路径行驶。连续规划的主要缺点是，由于规划道路网络的整个坐标范围需要密集的计算能力，道路或车道的表示可能会限制车辆的运动。

需要注意的是，上述用于规划的搜索空间表示技术并不总是独立使用的。例如，Voronoi图和势场被dolgovi et al。（2010a）生成安全轨迹。在大多数情况下，它们结合在一起，不仅是为了为单一的规划层次提供更好的结果，而且为了提供所有三个层次的规划能力（即路径、机动和轨迹规划）。表1总结了它们的优缺点。