五、时变电磁场

第五章 时变电磁场

一、时变电磁场的波动方程

1.波动方程的推导

思路：都是对旋度再求一次旋度

电场波动方程

$$ \nabla\times\nabla\times E=-\frac{\partial}{\partial t}(\nabla \times B)\\ \quad\quad\quad\quad\quad\quad=-\frac{\partial}{\partial t}\nabla \times(\mu H) $$ 再由 $$ \nabla\times\nabla\times E=\nabla(\nabla\cdot E )-\nabla^2E $$ 可得： $$ \nabla(\nabla\cdot E )-\nabla^2E=-\mu\frac{\partial}{\partial t}(J+\frac{\partial D}{\partial t}) $$ 带入 $$ \nabla\cdot E=\frac{\rho}{\varepsilon}\\D=\frac{\partial E}{\partial t} $$ 得到最后的波动方程： $$ \nabla^2E(r,t)-\varepsilon\mu\frac{\partial^2E(r,t)}{\partial t^2}=\mu\frac{\partial J(r,t)}{\partial t}+\nabla (\frac{\rho(r,t)}{\varepsilon}) $$

磁场波动方程

$$ \nabla^2H(r,t)-\varepsilon\mu\frac{\partial^2H(r,t)}{\partial t^2}=-\nabla \times J(r,t) $$ 注意： $$ v=\frac{1}{\sqrt{\varepsilon\mu}} $$

2.时变电磁场的势函数

目的：为了减少变量，方便求解

磁矢势与电标量

引入：
$$B(r,t)=\nabla \times A(r,t)$$
代入电磁感应式子：
$$\nabla \times [E(r,t)+\frac{\partial A(r,t)}{\partial t}]=0$$
(9)式中为无旋矢量场，可表示为变量函数的梯度
$$\begin{gathered} E(r,t)+\frac{\partial A(r,t)}{\partial t}=-\nabla \varphi (r,t) \\ E(r,t)=-\frac{\partial A(r,t)}{\partial t}-\nabla \varphi (r,t) \end{gathered}$$

$$A(r,t)为磁矢势\varphi (r,t)为电标势$$

时变电场由磁矢势和电标势共同描述

势函数规范及其方程

1. Coulomb规范：得到泊松方程

   有旋无散场

$$\nabla \cdot A(r,t)=0$$

2. Lorentz规范:得到达朗贝尔方程

$$\nabla \cdot A(r,t)+\epsilon \mu \frac{\partial \varphi (r,t)}{\partial t}=0$$

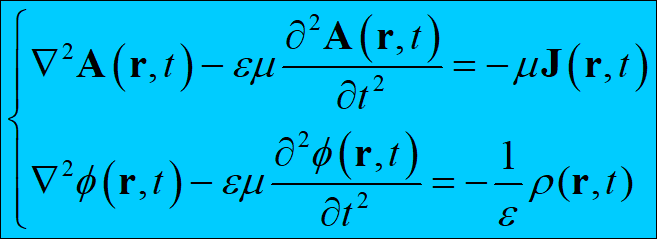
注意：不同的规范可以通过变换实现相互的转换

推迟势

上述波动方程的解为推迟势

二、 时变电磁场的能量

1.坡印廷矢量

表明：电磁场能量通过电磁场传播

能流密度：

$$S=\overrightarrow{e_n}\underset{\Delta s\to 0}{\lim }\frac{\Delta w}{\Delta S}$$

坡印廷矢量(电磁场能量流密度矢量)

​ 方向 —— 电磁能量传输的方向
$$\vec{S}(r,t)=\vec{E}\times \vec{H}$$

电磁场能量密度
$$w(r,t)=\frac{1}{2}[\mu H^2+\epsilon E^2]$$

坡印廷定理：闭合空间V内，电磁场能量守恒和转化的关系式。

单位时间内通过界面S进入V内的电磁场能量=单位时间内闭合区域V内电磁场能量的增量 +区域V内场对电荷系统所作的功
KaTeX parse error: Undefined control sequence: \ at position 34: …S(r,t) \cdot ds\̲ ̲=\iiint_{v}[\ve…

---

例1 双导线能量传输系统

$$\begin{gathered} \vec{E}=-\frac{U}{d}\vec{y} \\ \vec{H}=\frac{I}{a}\vec{x}(利用安培环路定理) \end{gathered}$$

---

【例2】同轴传输线内导线半径为a，外导线半径为b，两导线间为均匀绝缘介质 （如图)。导线载有电流I，两导线间的电压为U
（1）电场和磁场的计算
（2）能流密度矢量的计算
（3）传输功率的计算

三、唯一性定理

唯一性定理，表述如下：如果在闭合区域V 内，
①t=n 时刻的电磁场已知（初始条件).
② t>n  的任何时刻,电场或磁场在区域边界上的切向分量已知,或部分边界上电场和其余边界上的磁场切向分量已知（边界条件）.
则在t>=n 区域V 内存在唯一电磁场。

证明：反证法

假设有两组解 ：

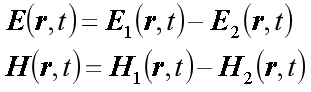
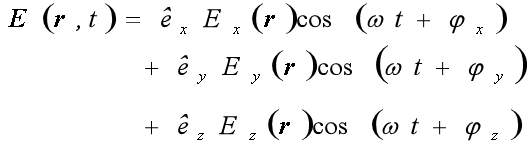
得出磁场能量减小。

四、谐变电磁场

什么是谐变电磁场？

随时间作简谐变化（同一频率）的电磁场称为谐变电磁场

为什么讨论和研究谐变电磁场？

（1）初始条件在任意时变情形下难以获取，而在谐变情形下，场量随时间作简谐变化 ，不存在场的初始状态。

（2）任意时变情形下，介质电磁参数特性复杂，难以推导出波动方程，求解困难。而在谐变情形下，电磁参数是常数。

1.介质的特性参数

$$\epsilon \mu 是与时间无关的，但是与频率有关$$

对于谐变电磁场，线性均匀各向同性介质的极化强度P(r,t)、磁化强度M(r,t)和传导电流密度J(r,t)也是谐变量

2.谐变电磁场的复数表示

电场可表示为：

瞬时表达式：

复向量表达式
$$\vec{E}(r)=Re({\vec{e}}_x{E}_x(\vec{r})e^{j{\varphi }_x}{e}^{jwt})+Re({\vec{e}}_y{E}_y(\vec{r})e^{j{\varphi }_y}{e}^{jwt})+Re({\vec{e}}_z{E}_z(\vec{r})e^{j{\varphi }_z}{e}^{jwt})$$
为了书写和表达方便，约定不写出
$$e^{jwt}$$
和圆点“ .”

eg4.5.1
做法：
（1）将正余弦函数变为余弦函数一次项，积化和差
（2）写成复指数形式
（3）将e^jwt项省去

3.谐变电磁场的麦克斯韦方程组

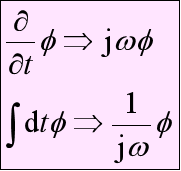
4.能量

谐变电磁场的坡印廷矢量

瞬时值

平均坡印廷矢量

eg2

5.谐变电磁场的波动方程

在谐变电磁场中，介质的特性参数 为常数，场量满足的波动方程为

波数

6.色散

​ 由于介质特性参数是频率的函数,不同频率的谐变电磁场在介质中传播速度v不同，波长也不相同。这一现象称为介质的色散，具有色散特性的介质称为色散介质。

g-DGNp1RXa-1650970250130)]

波数

[外链图片转存中…(img-Azzbu2Kn-1650970250130)]

[外链图片转存中…(img-ACzIAw6T-1650970250131)]

[外链图片转存中…(img-INbmeen1-1650970250131)]

6.色散

​ 由于介质特性参数是频率的函数,不同频率的谐变电磁场在介质中传播速度v不同，波长也不相同。这一现象称为介质的色散，具有色散特性的介质称为色散介质。