什么是深层神经网络、浅层神经网络——神经网络的数学基础原理(3)

一、什么是深度神经网络

上一篇文章我们讲到了不含激活函数的线性神经网络，这种网络一般来说是浅层神经网络，知道了在线性结构中，由于线性模型自身的局限性，线性深层神经网络变得没有意义，因为多个线性隐含层最终可以合并成单层。任意层的全连接神经网络和单层神经网络模型的表达能力没有任何区别。

本文介绍一下深层神经网络，也就深度神经网络或深度学习。区别于传统的浅层学习，深度学习的不同在于：

(1)强调了模型结构的深度，通常有5层、6层，甚至10多层的隐层节点。

(2)明确了特征学习的重要性。也就是说，通过逐层特征变换，将样本在原空间的特征表示变换到一个新特征空间，从而使分类或预测更容易。与人工规则构造特征的方法相比，利用大数据来学习特征，更能够刻画数据丰富的内在信息。

通过设计建立适量的神经元计算节点和多层运算层次结构，选择合适的输人层和输出层，通过网络的学习和调优，建立起从输入到输出的函数关系，虽然不能100%找到输入与输出的函数关系，但是可以尽可能的逼近现实的关联关系。使用训练成功的网络模型，就可以实现我们对复杂事务处理的自动化要求。

百度百科参考资料:https://baike.baidu.com/item/%E6%B7%B1%E5%BA%A6%E5%AD%A6%E4%B9%A0/3729729?fr=aladdin

二、深层神经网络与浅层神经网络特点及区别

第一部分介绍了深度神经网络的概念以及深度神经网络和浅层神经网络的区别。简单说，深层神经网络和浅层神经网络的区别在于网络中隐含层的层数多少。

上篇文章中讲过，神经网络层与层之间的数据传递算法，可以用线性代数中矩阵的乘法运算规则来表示。基于线性代数中矩阵的运算规则，推导出神经网络中，层数的多少取决于网络层是线性的还是非线性的。

文章链接：全连接网络的算法原理——神经网络的数学基础原理(2)

这里我们再来对比一下线性模型下的神经网络和非线性模型下的神经网络计算过程：

1.线性模型：

可以看到，在神经网络的线性层中，W(1)和W(2)是两个网络层的参数矩阵，根据矩阵乘法的结合律，W(1)和W(2)可以化简成W'，即多个线性层最终可通过化简，用一个线性层来表示。所以线性层构成的网络往往是浅层神经网络。

激活函数参考资料：激活函数和神经网络间的关系详解——神经网络的数学基础原理(1)

2.非线性模型：

可以看到，在神经网络的非线性层中，输入层 x 与隐含层W(1)进行矩阵的乘法运算后，计算结果还要再通过非线性函数(激活函数) f 进行一次转换，此时W(1)和W(2)不能再使用矩阵乘法的结合律进行化简，因此多层隐含层之间不能直接化简合并。

此时多层神经网络中的每一层隐含层开始变得有自己的意义，每一层都有了可以独立携带数据的部分特征，因此网络能储存的信息量也变得更大了，可以解决更加复杂的数据问题。

 

三、带有激活函数的神经网络计算过程

下面我们从图示的角度，理解引入非线性函数后的多层神经网络计算过程，笔记中隐藏层ai中使用了一个激活函数 f = max，表示从0和x中取较大值即：

                                                                             

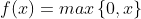
数据在带有激活函数的网络中传递计算过程如下：

 

四、总结

1.深度学习其实本质上指的就是利用深层神经网络进行机器学习

2.深层神经网络的重要特征就是网络的层数多，因此能携带更大的数据，可以实现更复杂的数据关系映射。

3.而实现多层网络结构就要通过在网络中使用非线性激活函数，使得神经网络可以任意逼近任何非线性函数，从而对各种函数关系进行拟合。

那是不是网络层数越多越好？网络结构越复杂越好？答案当然是否定的。后续我们来讨论一下，由于网络规模选择问题而导致的：过拟合、欠拟合、梯度消失、梯度爆炸等问题。

 

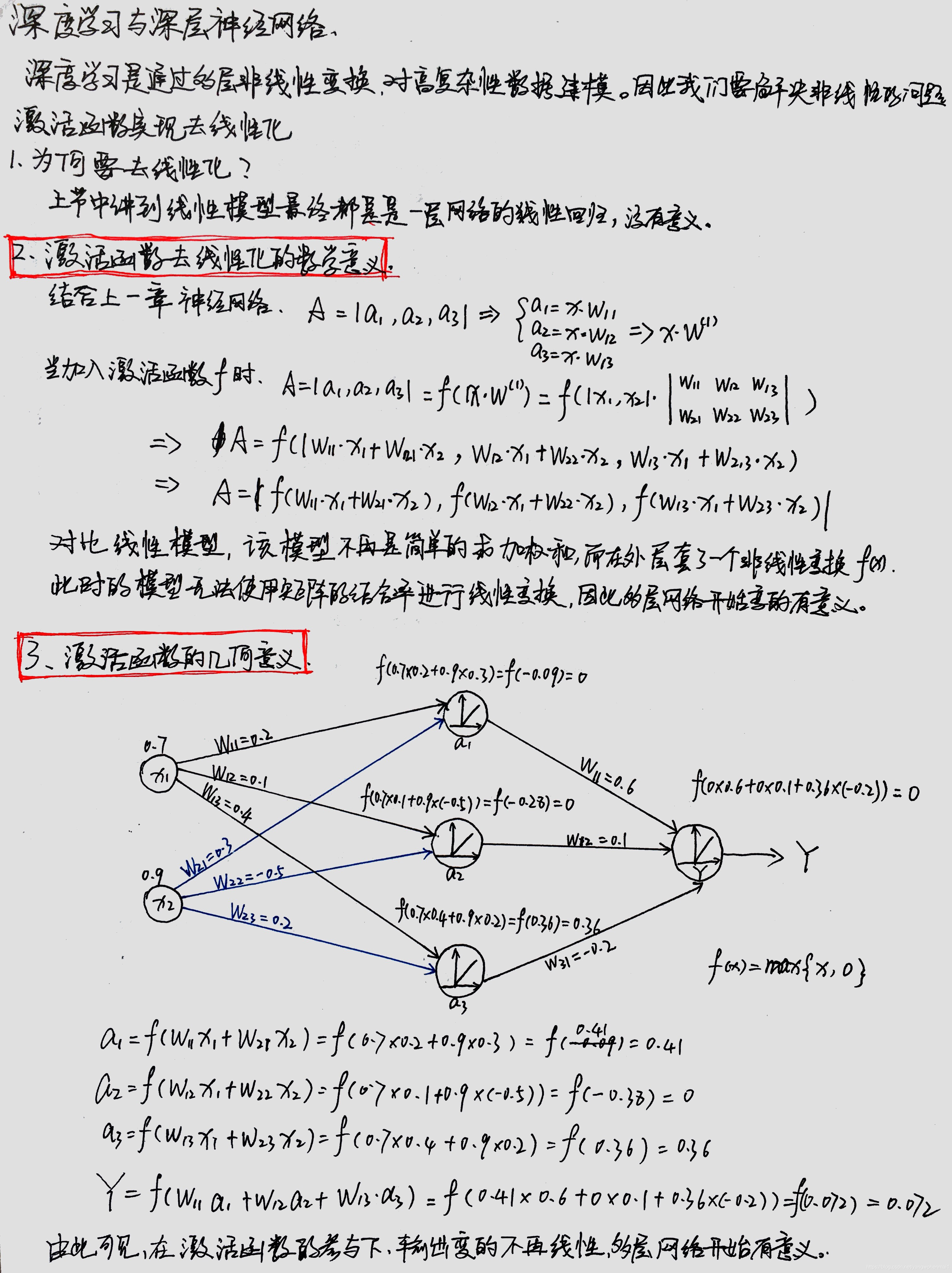
五、附学习笔记如下