点云PCA、KPCA算法原理、公式及示例

---

1 PCA算法

1 算法步骤：

设有$m$条$n$维数据。

1）将原始数据按列组成$n$行$m$列矩阵$X$

2）将X的每一行（代表一个属性字段）进行零均值化，即减去这一行的均值

3）求出协方差矩阵$$C=\frac{1}{m}X{X}^T$$

4）求出协方差矩阵$C$的特征值及对应的特征向量

5）将特征向量按对应特征值大小从上到下按行排列成矩阵，取前$k$行组成矩阵$P$

6）$Y=PX$即为降维到k维后的数据

2 示例

有原数据组成的矩阵如下，用PCA方法将这组二维数据其降到一维。

因为这个矩阵的每行已经是零均值，这里我们直接求协方差矩阵：

然后求其特征值和特征向量(标准化)为

因此我们的矩阵P是：

最后我们用$P$的第一行乘以数据矩阵，就得到了降维后的表示：

3 代码

//基于Eigen库实现PCA，此代码经本人调试完成，未出现错误
//示例数据：5个2维数据   
/* 
1 1
1 3
2 3
4 4
2 4
*/

#include <iostream>
#include <algorithm>
#include<cstdlib>
#include <fstream>
#include <Eigen/Dense>

using namespace std;
using namespace Eigen;

MatrixXd featurnormal(MatrixXd &X)
{
	// Eigen:基本功能
	// VectorXd    等价于Matrix<double,Dynamic,1>;       //列向量，一列
	// RowVectorXd 等价于Matrix<double,1,Dynamic>;       //行向量，一行
	// MatrixXd    等价于Matrix<double,Dynamic,Dynamic>;

	//计算每一维的均值
	MatrixXd X1 = X.transpose();  //先来个普通转置【行列变换】

	VectorXd meanval = X1.rowwise().mean();//colwise按列求均值。//rowwise按行求均值。 //X1.rowwise()不可用
	cout << "meanval" << endl << meanval << endl;
	
	//样本均值化为0	
	X1.colwise() -= meanval;   //按列减，每一列与均值做差
	
	return X1;
}

void ComputeCov(MatrixXd &X1, MatrixXd &C)
{
	//计算协方差矩阵设我们有m个n维数据记录，将其按列排成n乘m的矩阵X，设C =X*XT/m
    //此处除以m，具体原因你深思[可参考此文](https://blog.csdn.net/hustqb/article/details/78394058)
		
	C = X1*X1.adjoint();//相当于原始数据XT*X    adjiont()求伴随矩阵 相当于求矩阵的转置
	/*cout << "C:" << endl << C<< endl;*/
	C = C.array() / X1.cols();//C.array()矩阵的数组形式  ///逐元素除以m

	cout << "C:" << endl << C << endl;
}

void ComputEig(MatrixXd &C, MatrixXd &vec, MatrixXd &val)
{
	//计算特征向量和特征值 SelfAdjointEigenSolver自动将计算得到的特征向量和特征值排序
	SelfAdjointEigenSolver<MatrixXd> eig(C);
	//所求特征向量依据对应的特征值从小到大排列。
	vec = eig.eigenvectors();
	val = eig.eigenvalues();
	
	//故应该依靠翻转将特征向量依据特征值从大到小排列。【如下】
	vec.colwise().reverse();
	cout << "***************************************" << endl;
	cout << "vec.colwise().reverse():" << endl << vec.colwise().reverse() << endl;
	cout << "***************************************" << endl;
	val.colwise().reverse();
	cout << "val.colwise().reverse():" << endl << val.colwise().reverse() << endl;
	cout << "***************************************" << endl;
}

// 计算维度
int ComputDim(MatrixXd &val)
{
	int dim;
	double sum = 0;
	for (int i = val.rows() - 1; i >= 0; --i)
	{
		sum += val(i, 0);
		dim = i;
		if (sum / val.sum() >= 0.8)//达到所需要的要求时
			break;
	}
	//cout << val.rows() - dim << endl;
	return val.rows() - dim;
}

int main()
{
	//文件操作   文件路径使用： \\ 或者 /
	ifstream fin("F:\\PCLprincipal\\pca070808\\Project1\\m5n2.txt");
	if (fin.is_open())
	{
		cout << "载入成功" << endl;
	}
	ofstream fout("X1X2outpot1.txt");

	//定义所需要的量
	const int m = 5, n = 2, z = 2;
	MatrixXd X(m, n), C(z, z);  //C为协方差阵
	MatrixXd vec, val;

	//读取数据
	double in[z];
	for (int i = 0; i < m; ++i)
	{
		for (int j = 0; j < n; ++j)
		{
			fin >> in[j];  //单值读入
		}
		for (int j = 1; j <= n; ++j)
			X(i, j - 1) = in[j - 1];
	}

	cout << endl;
	cout << "X为原始的数据：" << endl << X << endl;
	cout << endl;
	
	// 1 均值0标准化
	MatrixXd X1 = featurnormal(X);
	cout << "X1均值0标准化的数据：" << endl << X1.transpose() << endl;   ///.transpose()方便为了查看 N*3
	cout << endl;

	// 2 计算协方差
	ComputeCov(X1, C);

	// 3 计算特征值和特征向量
	ComputEig(C, vec, val);

	// 4 计算损失率，确定降低的维数
	int dim = ComputDim(val);
	//int dim = 1;
	// 5计算结果

	//但当涉猎
	//MatrixXd res001 = vec.transpose().rightCols(dim).transpose();
	//MatrixXd res001 = vec.bottomRows(dim);
	//MatrixXd res001 = vec.transpose().leftCols(dim).transpose();
	/*cout <<"X.colwise().reverse()"<<endl<< X.colwise().reverse() << endl;*/ //垂直翻转，优秀的很，

	MatrixXd res001 = vec.colwise().reverse().topRows(dim);  
	//按列翻转取前dim行 特征向量，实现依据特征值从大到小排列获取特征向量。
	
	cout << "res001:" << endl << res001 << endl;  //2*3
	MatrixXd res = res001*X1; //2*3  *  N*3  Y=PX 此Y即为降维之后的结果。

	//方便查看
	cout << "res为用PCA算法之后的数据：" << endl << res.transpose() << endl;
	
	// 6输出结果
	fout << "the result is" << res.rows() << "x" << res.cols() << "after pca algorithm" << endl;
	fout << res.transpose();
	fout.close();
	
	system("pause");
	return 0;
}

2、KPCA

参考链接：https://www.bilibili.com/video/BV1ex41157bH/?spm_id_from=333.337.search-card.all.click&vd_source=1e477975f47c97c1afd2d9d84c34de3d该视频的0:34:52处理开始

高维空间的PCA：

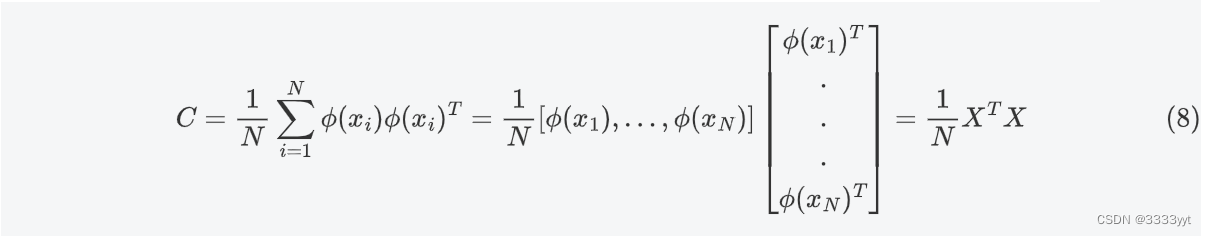
由核函数，可得如下公式：

$K=X{X}^T$得特征方程为
$$\begin{gathered} (X{X}^T)u=\lambda u \\ \Rightarrow X^T(X{X}^T)u=\lambda X^{T}u \\ \Rightarrow (X^{T}X)(X^{T}u)=\lambda (X^{T}u) \end{gathered}$$
可知，$X^{T}u$是$X^{T}X$的特征向量。但是，它的模不是1。

$X^{T}X$的特征向量$v$可由$K=X{X}^T$的特征值计算：
$$\begin{gathered} v=\frac{1}{||X^{T}u||}{X}^{T}u=\frac{1}{\sqrt{u^{T}X{X}^{T}u}}{X}^{T}u \\ =\frac{1}{\sqrt{u^{T}Ku}}{X}^{T}u=\frac{1}{\sqrt{u^T\lambda u}}{X}^{T}u \\ =\frac{1}{\sqrt{\lambda }}{X}^{T}u \end{gathered}$$
其中，$u^{T}u=1$。

测试样本$\varphi (x^{’})$的某一个方向的投影可以由下式计算