本文深入探讨了拉格朗日中值定理在解决极限问题时的妙用，通过一个具体的例子展示了如何利用拉式中值简化复杂计算。文章指出，理解拉式中值的本质、适用条件及其应用方法是关键，包括夹逼定理和等价参数两种策略。通过夹逼定理，当内层函数趋于相同值时，可以确定参数的范围；而等价参数法适用于内层函数趋于0或无穷的情况。此外，还提供了三个具体的极限问题作为练习，帮助读者巩固这一技巧。
懂不懂拉式中值，在解极限的时候，是两重境界。用一个例题来体会，自行感受。
题目：
lim
x
→
0
c
o
s
(
s
i
n
x
)
−
c
o
s
x
x
4
\lim_{x \rightarrow 0}{\frac{cos(sinx)-cosx}{x^{4}}}
limx→0x4cos(sinx)−cosx
当你不会拉式中值的时候，你的解答如下：
可见不用拉式中值的解答，又臭又长！
但是当你会拉式中值时，你的解答是这样：
运用拉式中值解决极限
三步解决问题它不香么？别人还在写的时候，我的结果都已经口算出来了！
那么这种化劲是怎么练出来的？学长就带你研究！！！
对于数学中的性质和公式，一般我们从三个方面去思考：
1.这个公式是什么(本质)；
2.这个公式什么时候用；
3.这个公式怎么用。
1.这个公式是什么
首先回归定理：
f
(
x
1
)
−
f
(
x
2
)
=
f
′
(
ξ
)
(
x
1
−
x
2
)
f(x_{1})-f(x_{2})=f'(\xi)(x_{1}-x_{2})
f(x1)−f(x2)=f′(ξ)(x1−x2)，其中
ξ
\xi
ξ介于
x
1
x_{1}
x1与
x
2
x_{2}
x2之间
上式
x
1
、
x
2
x_{1}、x_{2}
x1、x2 是个数，如果推广为函数呢？
f
[
g
(
x
)
]
−
f
[
h
(
x
)
]
=
f
′
(
ξ
)
[
g
(
x
)
−
h
(
x
)
]
f[g(x)]-f[h(x)]=f'(\xi)[g(x)-h(x)]
f[g(x)]−f[h(x)]=f′(ξ)[g(x)−h(x)]，其中
ξ
\xi
ξ介于
g
(
x
)
g(x)
g(x)与
h
(
x
)
h(x)
h(x)之间
这就是上面应用拉氏中值求极限的核心：两个复合函数作差变成了内层函数作差，这就相当于将原来的两个复合函数的皮(外层函数f相当于皮)给剥掉了。这样的话，就能起到化繁为简的目的，这就是拉氏中值。
2.什么情况下用？
公式中有两处细节：a.复合函数作差；b.外层函数一致。所以，满足这两个条件，就可以马上掏出拉氏中值试一试。
3.怎么用？
数学做题的过程就是化繁为简，变未知到已知的过程。我们还是从第一点拉氏中值的本质入手，观察下这个式子：
我们最终是通过拉氏中值转化到右边的式子，如果右边的式子可以求出来，那么我们的工作就完成了，拉氏中值也完成了它得使命。但是可不可以求出来呢？我们观察一下：右边式子中
f
′
(
x
)
,
g
(
x
)
,
h
(
x
)
f'(x),g(x),h(x)
f′(x),g(x),h(x) 都是可以找出来或者求出来，而参数
ξ
\xi
ξ却让人为难，我们只知道参数
ξ
\xi
ξ的一个范围，但是具体是多少不一定清楚。所以这里就是一个关键问题，也是衡量拉氏中值能不能顺利做下去的命门：参数搞不搞的定！
那么参数如何搞定呢？一般有两个思路：a.夹逼定理；b.等价于某个关于x的式子。
a.夹逼定理：
我们知道了参数 ξ \xi ξ的一个范围，它是在 g ( x ) g(x) g(x) 和 h ( x ) h(x) h(x) 之间，假设 g ( x ) ≥ h ( x ) g(x)\geq h(x) g(x)≥h(x) ，那么就有 h ( x ) ≤ ξ ≤ g ( x ) h(x)\leq \xi\leq g(x) h(x)≤ξ≤g(x) ,是不是有点夹逼定理的味道了？如果取极限后 g ( x ) g(x) g(x) 和 h ( x ) h(x) h(x)相等，那么参数 ξ \xi ξ就可以夹出来了。
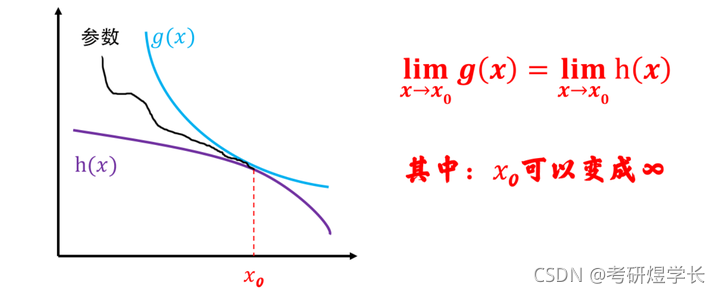
话不多说，直接上题，彻底搞定这个思路：
本题中
g
(
x
)
g(x)
g(x)和
h
(
x
)
h(x)
h(x)都趋近于1，因此通过夹逼定理得到参数
ξ
\xi
ξ也趋近于1，然后直接带进
f
′
(
x
)
f'(x)
f′(x)中(代入后不为∞也不为0)，就可以正常解出这个极限。
所以有本方法的适用范围：
g
(
x
)
g(x)
g(x)和
h
(
x
)
h(x)
h(x)都趋近于
x
0
x_{0}
x0 ，同时
lim
x
→
x
0
f
′
(
x
)
\lim_{x \rightarrow x_{0}}f'(x)
limx→x0f′(x)存在且不为0。
不适用范围：如果
g
(
x
)
g(x)
g(x)和
h
(
x
)
h(x)
h(x)都趋近于0（或∞），且
lim
x
→
0
(
或
∞
)
f
′
(
x
)
\lim_{x \rightarrow 0(或∞)}{f'(x)}
limx→0(或∞)f′(x) 为
∞
∞
∞或者
0
0
0，这时候夹逼定理得参数
ξ
\xi
ξ的值就不再适用了，尝试使用方法b搞。
b.等价于某个关于x的式子：
适用于：当内层函数趋近于0，同时
x
→
0
,
f
′
(
x
)
～
m
x
k
x \rightarrow 0,f'(x)～mx^{k}
x→0,f′(x)～mxk （其中
m
，
k
m，k
m，k为非0常数）
或者当内层函数趋近于∞，同时
x
→
∞
,
f
′
(
x
)
～
m
x
k
x \rightarrow ∞,f'(x)～mx^{k}
x→∞,f′(x)～mxk （其中m，k为非0常数）
上述条件看似很严格，但是所幸在考研极限题目中，基本上都是满足的，本文所选取的极限也是满足的。所以其作为一个隐含条件在过程中就没有体现。严谨的小伙伴可以在用该方法求极限之前稍微判定一下。
该方法如何做？
如果
h
(
x
)
h(x)
h(x) 和
g
(
x
)
g(x)
g(x) 的极限趋近于无穷或者趋近于0，则需要判断一下
lim
x
→
x
0
h
(
x
)
g
(
x
)
\lim_{x \rightarrow x_{0}}{\frac{h(x)}{g(x)}}
limx→x0g(x)h(x) 是否为1？如果是1。就可以将参数
ξ
\xi
ξ等价于一个函数，再带入求极限。而这个函数处于
h
(
x
)
h(x)
h(x) 和
g
(
x
)
g(x)
g(x)之间就可以。抽象？直接上题。
一道简单的拉式中值，判定结果为1之后运用等价求参数
这道题看见两个内层函数趋近于无穷，所以我们判定
lim
x
→
x
0
h
(
x
)
g
(
x
)
=
1
\lim_{x \rightarrow x_{0}}{\frac{h(x)}{g(x)}}=1
limx→x0g(x)h(x)=1 后，就可以把参数等价为
x
2
x^{2}
x2 ，进而得出结果。(本文开头的题目也是这样的思路)。也许你疑惑：为什么这样判定？判定后为啥可以这样设？
数学证明来解释这一点：
1.首先证明参数 ξ 和 h ( x ) 与 g ( x ) \xi 和 h(x) 与 g(x) ξ和h(x)与g(x) 之间的函数等价：
2.再证明 f ′ ( ξ ) f'(\xi) f′(ξ) 与 f ′ ( y ( x ) ) f'(y(x)) f′(y(x)) 等价(其中 y ( x ) y(x) y(x) 为 h ( x ) h(x) h(x) 与 g ( x ) g(x) g(x) 之间的函数)：
注：若此时
h
(
x
)
h(x)
h(x)和
g
(
x
)
g(x)
g(x)趋近于∞，证法相似。
如果找不到介于
h
(
x
)
h(x)
h(x) 和
g
(
x
)
g(x)
g(x) 之间的函数，可以直接令
f
′
(
ξ
)
f'(\xi)
f′(ξ)等价于
f
′
(
g
(
x
)
)
f'(g(x))
f′(g(x)) 或
f
′
(
h
(
x
)
)
f'(h(x))
f′(h(x)) 。
于是就有了如下精简拉氏中值秒杀结论：
补充两点：
1.对于数列极限，也可以运用拉氏中值求解，只不过需要在运用之前将数列转变为函数，即
n
→
x
n\rightarrow x
n→x ，即可。
2.方法b及相应的结论在计算小题时，可以快速得到答案；对于大题而言，可以用这个方法及结论快速判断能否用拉氏中值，同时可以利用这个方法快速验算自己的结果。如果想要在大题中使用方法b，则具体步骤要写的详细一点（利用夹逼定理），如下例题。
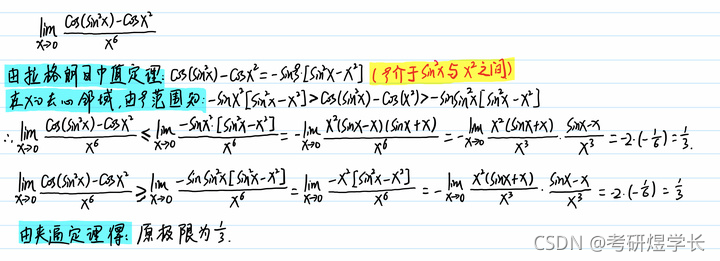
总结一下：
1.看见复合函数相减(有些相加可以通过变形变成相减)就要考虑到拉式中值。
2.并不是所有复合函数相减都能用拉式中值，主要看参数能不能求出来。
3.求出参数的方法有两种，一个是夹逼定理；一个就是将参数等价为关于x的式子。
趁热打铁：
1.
lim
x
→
∞
x
2
(
a
r
c
t
a
n
a
x
−
a
r
c
t
a
n
a
x
+
1
)
\lim_{x \rightarrow \infty}{x^{2}(arctan\frac{a}{x}-arctan\frac{a}{x+1})}
limx→∞x2(arctanxa−arctanx+1a) 其中a大于0
2.
lim
x
→
2
5
x
−
1
−
2
x
+
5
x
2
−
4
\lim_{x \rightarrow 2}{\frac{\sqrt{5x-1}-\sqrt{2x+5}}{x^{2}-4}}
limx→2x2−45x−1−2x+5
3.
lim
x
→
0
l
n
(
1
+
x
2
)
−
l
n
(
1
+
s
i
n
2
x
)
x
4
\lim_{x \rightarrow 0}\frac{ln(1+x^{2})-ln(1+sin^{2}x)}{x^{4}}
limx→0x4ln(1+x2)−ln(1+sin2x)
到此结束~
我是煜神学长，考研我们一起加油！！！
关注TB店铺：KY煜神思维导图，了解考研数学提分利器思维导图
扫一扫
4473
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
