19 含参量积分

1 含参量正常积分

• 本章开始讨论多元函数各种积分问题,先研究含参量积分.
• $f(x,y)$定义在$R=[a,b]\times [c,d]$上的二元函数
• 当$x$取$[a,b]$上某定值时,
  • $f(x,y)$则是定义在$[c,d]$上以$y$为自变量的一元函数
  • 若这时$f(x,y)$在$[c,d]$上可积
  • 则其积分值是$x$在$[a,b]$上取值的函数

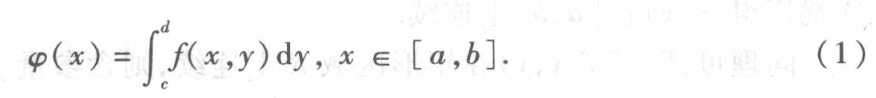
这儿是空的

定理19.1（连续性）

这儿是空的

定理19.2（连续性）

这儿是空的

定理19.3（可微性）

这儿是空的

定理19.4（可微性）

这儿是空的

定理19.5（可积性）

这儿是空的

定理19.6（可积性）

这儿是空的

2 含参量反常积分

这儿是空的

一 一致收敛性及其判别法

这儿是空的

定义1

• 若含参反常积分(1)与$\Phi (x)$对任给的$\epsilon >0$,
• 总存$N>c$,使得当$M>N$时,对一切$x\in [a,b]$
• 都有
  $$|{\int }_c^{M}f(x,y)dy-\Phi (x)|<\epsilon$$
• 即
  $$|{\int }_M^{+\infty }f(x,y)dy|<\epsilon$$
• 则称(1)在$I$上一致收敛于$\Phi (x)$,
• 或说(1)在$I$上一致收敛

theorem 19.7 一致收敛的柯西准则

• (1)在$I$上一致收敛的充要是
• 对任给$\epsilon >0$。
• 总存在某一实数$M>c$,使得当$A_1,A_2>M$时,对一切
  $x\in I$,都有
  $$|{\int }_{A_1}^{A_2}f(x,y)dy|<\epsilon \text{\hspace{1em}(3)}$$
• 由定义1,还有以下含参积分一致收敛的判别准则

定理19.8

• 含参量在$I$上一致收敛的充要:
  $$\underset{A\to +\infty }{\lim }F(A)=0$$
  $$F(A)=\underset{x\in I}{\sup }|{\int }_A^{+\infty }f(x,y)dy|$$

例1

• 证
  $${\int }_0^{+\infty }\frac{\sin xy}{y}dy\text{\hspace{1em}(4)}$$
• 在$[\delta ,+\infty )$上一致收敛($\delta >0$)
• 但$(0,\infty )$内不一致

证

这儿是空的

定理19.9

• (1)在$I$上一致收敛的充要:
• 对任一趋于$+\infty$的递增列 { A n } \{A_n\} {An​},$A_1=c$
• 函数项级数
  $$\sum _{n=1}^{+\infty }{\int }_{A_n}^{A_{n+1}}f(x,y)dy=\sum _{n=1}^{\infty }{u}_n(x)\text{\hspace{1em}(6)}$$
• 在$I$上一致收敛

证

这儿是空的

魏尔斯特拉斯M判别法

• $g(y)$,使
  1$$|f|\le g,(x,y)\in I\times [c,+\infty )$$
• 若${\int }_c^{\infty }gdy$收敛
• 则${\int }_c^{\infty }f(x,y)dy$在$I$上一致收

狄屎

• 对一切$N>c$,含参量正常
  $${\int }_c^{N}f(x,y)dy$$
• 对参量$x$在$I$上一致有界
  • 即存在正数$M$
  • 对$\forall N>c\forall x\in I$
  • 有
    $$|{\int }_c^{N}f(x,y)dy|\le M$$
• 每个$x\in I$
  • $g(x,y)$关于$y$是单减
• 且当$y\to \infty$时,对参量$x$
  • $g(x,y)$一致收敛于0

阿贝尔

• ${\int }_c^{+\infty }f(x,y)dy$在$I$上一致收敛
• 对每个$x$,$g$为$y$的单,
• 且对参量$x$,$g(x,y)$在$I$上一致有界

例2

这儿是空的

二 含参量反常积分的性质

这儿是空的

3 欧拉积分

这儿是空的

一 $\Gamma$函数

这儿是空的

二 $\mathrm{B}$函数

这儿是空的

三 $\Gamma$函数与$\mathrm{B}$函数之间的关系

这儿是空的