神经网络学习笔记（三） 梯度下降法

梯度下降法

在上一张，我们学习过了LMS算法，就是利用了著名的梯度下降法，但是LMS算法只是一种特殊的实现，是均方差这个特定函数的梯度下降，这次我们来看一下梯度下降对普通函数求极值的一些应用。

我们来试一下二次函数的极值点求法。

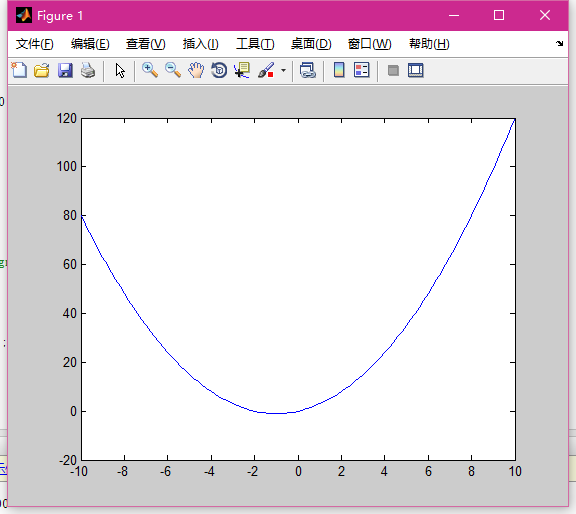
首先我们建立一个二次函数：
y=x^2+2*x

这个极值大家应该知道 x取-1就可以得到极小值。

我们来编写一个梯度下降法来求极值点：

x=50;
% y=x^2;


sigma=0.9;
yr=10^5;

for i=1:100000;
    y=x^2+2*x;
    if abs(y-yr)<10^-100
        break;
    end

    x=x-sigma*(2*x+2);

    yr=y;

%     sigma=0.9999^i*sigma;
end


fprintf('迭代次数 %d',i);

前一节误差的迭代就是x的步长。

得到结果：

非常准确。

但是梯度下降法有个严重的问题！！

容易陷入局部最小值！！！！

下面我们来试一试局部最小值问题：

建立一个函数：
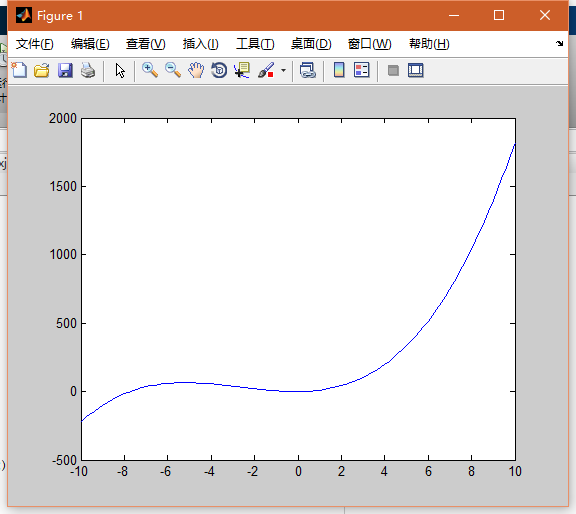
y=x^3+8*x^2+2*x
这个函数的图形如下图：

在0点附近有极值点，但不是最小值点。

x=50;
% y=x^2;


sigma=0.005;
yr=10^5;

for i=1:10000;
    y=x^3+8*x^2+2*x;
    if abs(y-yr)<10^-100
        break;
    end

    x=x-sigma*(3*x^2+16*x+2);
    x
    yr=y;

%     sigma=0.9999^i*sigma;
end


fprintf('迭代次数 %d',i);

我们利用梯度下降法来测试，在学习率比较低的情况下会发现：

迭代到了极值点，这就是梯度下降法的缺点！

结束语

虽然梯度下降法可以有效的快速收敛，但当函数越来越复杂以后，会特别容易收敛到非最小值点，这就需要有一个更加好的初值和更加合适的学习率。