将信号进行小波包分解的过程本质上是一个小波函数的低通、高通滤波器与数字信号之间进行卷积运算的过程,这里的卷积运算有别于卷积神经网络层中的“卷积”操作,是数学定义上的运算操作,这点在很多文章中都有体现。下图举例说明了在卷积神经层和数学定义中卷积操作的异同。从图中可以发现,通过反转卷积核的权值顺序,两者之间的卷积操作可以很容易地进行切换,如果将图(a)中卷积核参数的位置进行翻转,将K3处在原先的K0的位置,K2处在原先的K1的位置,K1处在原先K2的位置,K0在原先的K3的位置,那么图(a)中的卷积结果便会等于图(b)的结果,反之亦然。在了解卷积神经网络层能以翻转卷积核参数的方式实现数学意义上的卷积运算后,很自然地联想到可以利用一维卷积神经层来实现对输入信号的小波包变换。


考虑到小波包变换与卷积神经网络层在实现细节上的相似性,可以构建一种特殊的卷积神经网络层,来实现原始信号在分类模型内部的时频域转换。将小波包变换以卷积层的形式植入神经网络结构中的目的不仅是为了提高分类方法的整体性和可植入性,更是考虑到卷积层能够通过梯度反向传播算法自主训练,从而赋予时频域分析方法自适应诊断任务、提升分解质量、增强与分类模型的适应度等重要能力。
小波包系数是通过信号序列与两个小波滤波器进行卷积运算获得的,现假设已经选定好了一个小波函数,并且它的小波滤波器系数的长度为2 ,则一个单层的小波包变换可以下图形式实现。
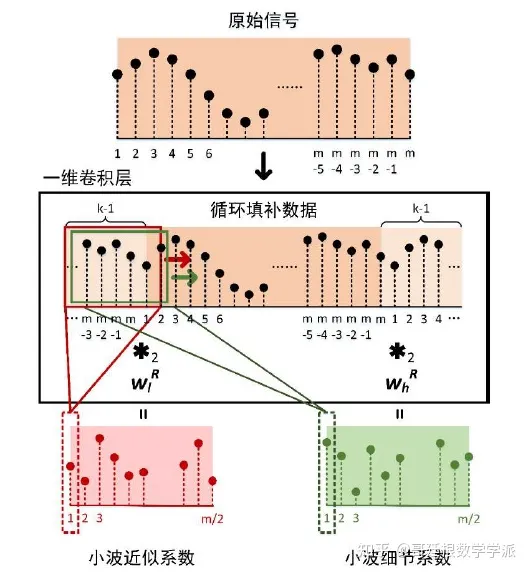
为了实现图中的多层小波包变换过程,需要将图上图中的一维卷积层改成递归一维卷积层的形式,即不断地将原始输出重新反馈回卷积层结构中,并不断生成下一层分解系数。

当信号需要进行p层的小波包分解时,一维卷积层的递归次数要设定为p次,上图中的递归一维卷积层每次运算后的输出数量都会变成输入数量的两倍,这点与常见的递归卷积层不同,但并不额外增加编程实现的难度。
mbd.pub/o/GeBENHAGEN
擅长现代信号处理(改进小波分析系列,改进变分模态分解,改进经验小波变换,改进辛几何模态分解等等),改进机器学习,改进深度学习,机械故障诊断,改进时间序列分析(金融信号,心电信号,振动信号等)







 文章探讨了小波包分解作为信号处理的一种方法,其过程可以看作是数学卷积。通过对比卷积神经网络层中的卷积操作,提出可以构建特殊卷积层在神经网络内部实现小波包变换,以增强分类模型的性能和适应性。这种方法允许信号在分类过程中进行时频域转换,并能通过反向传播自动优化小波包系数,适用于故障诊断等领域。
文章探讨了小波包分解作为信号处理的一种方法,其过程可以看作是数学卷积。通过对比卷积神经网络层中的卷积操作,提出可以构建特殊卷积层在神经网络内部实现小波包变换,以增强分类模型的性能和适应性。这种方法允许信号在分类过程中进行时频域转换,并能通过反向传播自动优化小波包系数,适用于故障诊断等领域。
















 3万+
3万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








