刚体的定轴转动定律推导

牛顿第二定律＋微元法

情景如图1，该不规则物体M受外力F（当然不只有一个外力，我们先只讨论一个，后面可以推广到多个力）绕一个定轴L旋转。那么如何求出物体的转动情况呢？一眼看去，我们很难从整体直接受力分析，那么不如从一个很小的点（微元法，很重要的一个研究方法）去找规律。这既然是运动，那么我们可以从牛顿第二定律入手。

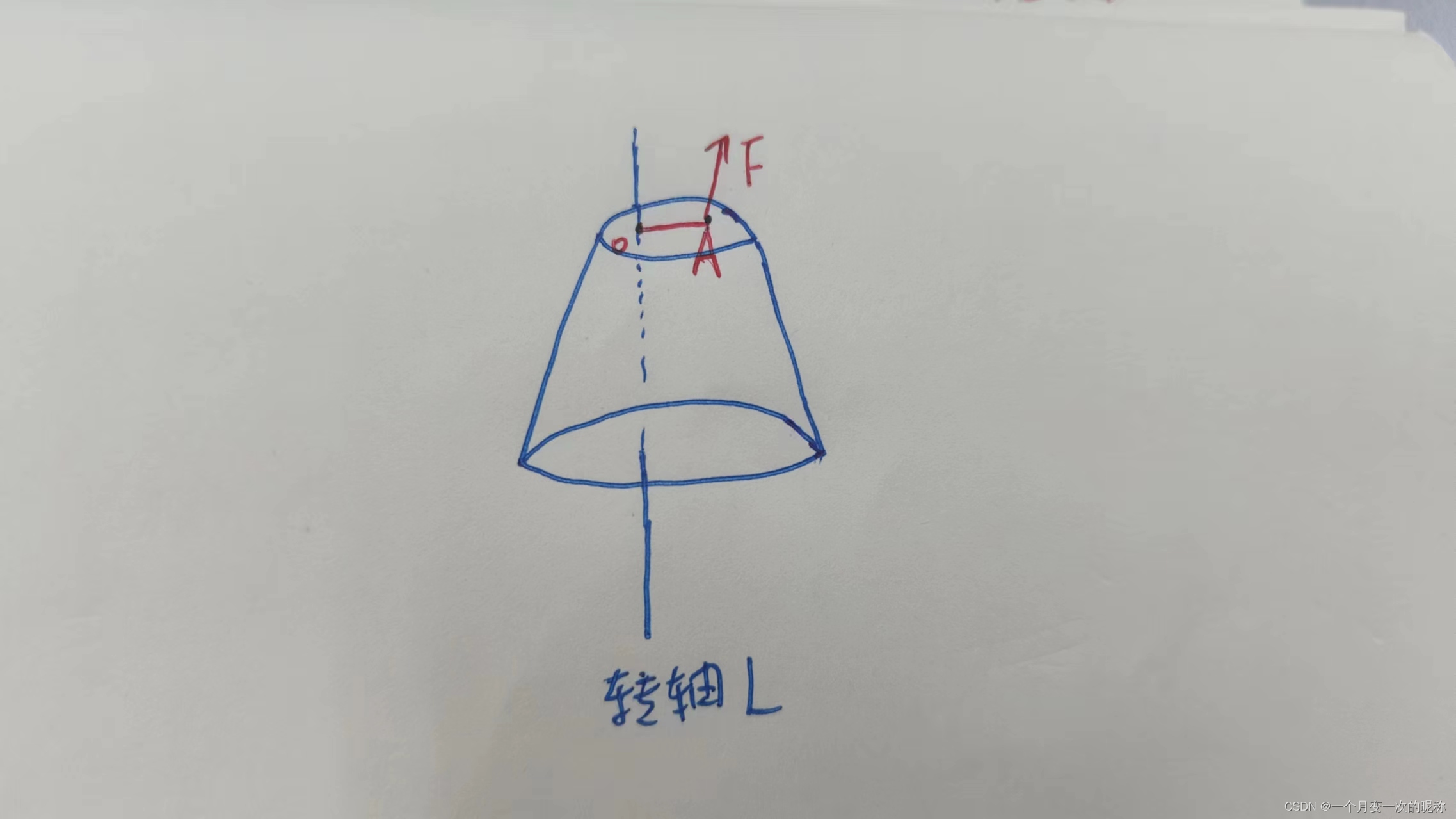
图1

对于该微小物体A（几乎可以看成一个点）受力分析。并且该点所受的合外力有两个作用，一个是改变速度的大小，一个是改变速度的方向，由此可以写出1式。

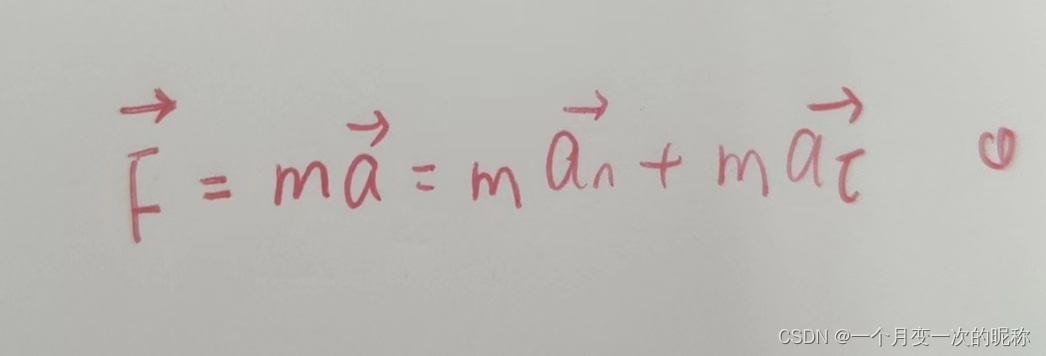
1式

由圆周运动知识可知，径向加速度an大小等于带入，并将矢量和写成单位向量乘以模的形式。然后值得声明清楚的一点就是，微元A的外力F其实本质上可以分为内力（来物体M内部的作用力）和外力(来物体M外部的作用力)，当然内力不止一个，所以用表示，于是带入1式可以得到2式。

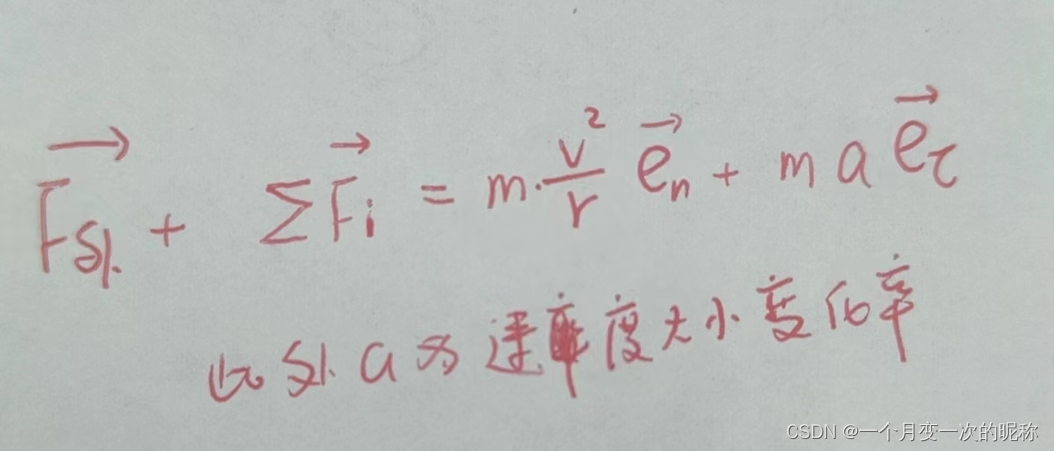
2式

我们先声明一点，向量r就是该点到转轴的位置矢量【转轴1指向该点形成的向量】，是切向单位向量，是径向单位向量。等式左右两边同时叉乘位置矢量r，于是得到3式

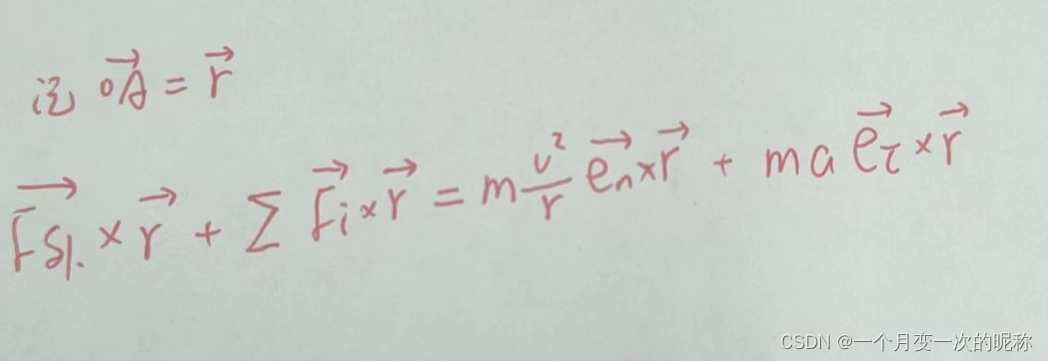
3式

与r这两个向量方向平行，所以叉乘结果是0。与r垂直，所以叉乘之后的大小是r【标量形式】

所以等式右边只剩下mar，然而这样的化简还不够，这里a是速度大小的变化率，对于每个微元的速度变化率是不一样的，所以应该从中提取一个不变量β【角加速度】，顾名思义，就是角速度随时间的变化率，β这不是凭空而来，是4式推导得来的。

推导如下：

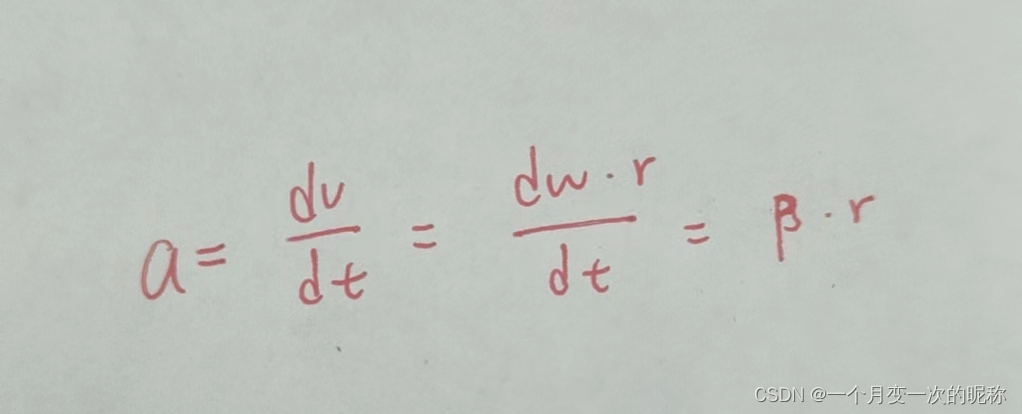
4式

 从4式可以看出，β是随时间的变化率，将3式子中的a用4式代换之后，等号右边式子变成m乘β。所以到目前为止，式子整理成如5式.

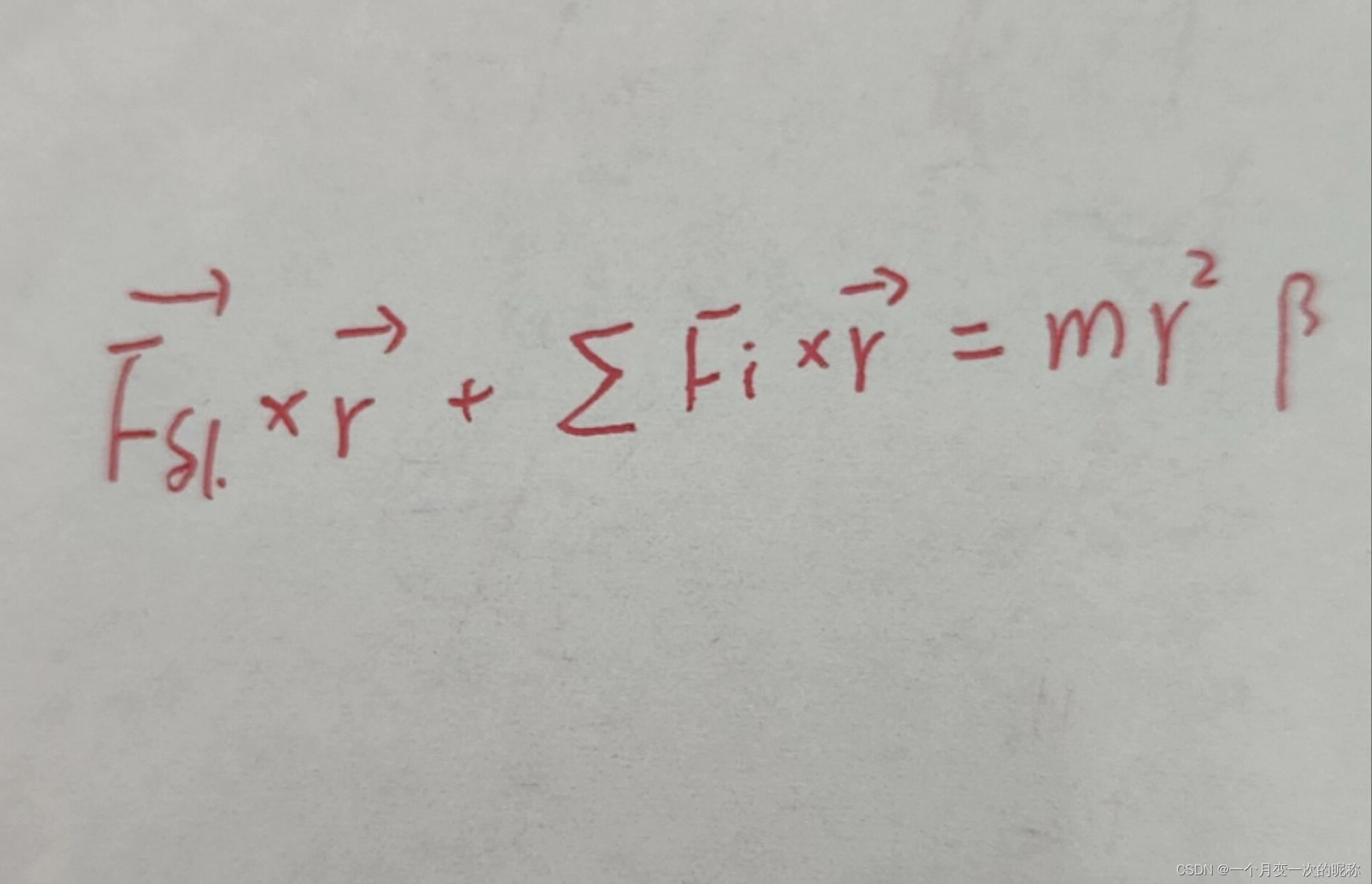
5式

这个等式的物理意义就是，该微元所受外力F 叉乘r +该微元所受所有Fi叉乘r     =m乘以角加速度。换言之就是：该微元的内力的力矩加上外力的力矩等于mβ

上个式子就仅仅讨论一个微小物体，对于整体物体来说，就是无数微元的累积，即左右等式累加得。

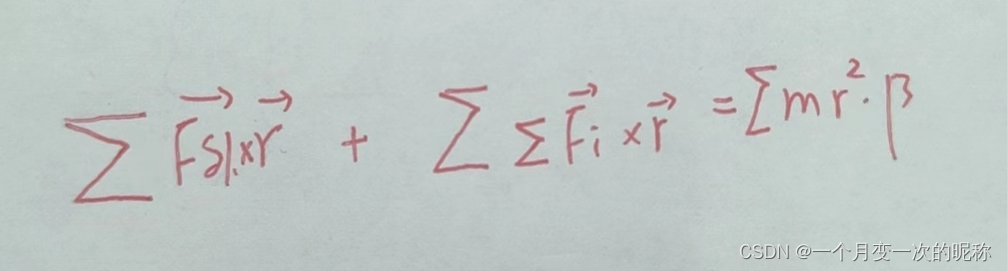
左边等号的第二个式子的物理意义就是所有微元之间所有相互作用力的力矩，就是物体内部所有的相互作用力的力矩，然而相互作作用力是成双出现的并且共线且方向相反，即有作用力f必有反作用力-f，所以等号左边第二个式子还可以理解为物体内部所有作用力和反作用力的力矩的累积。根据叉乘的理解这第二项式子必然为0。

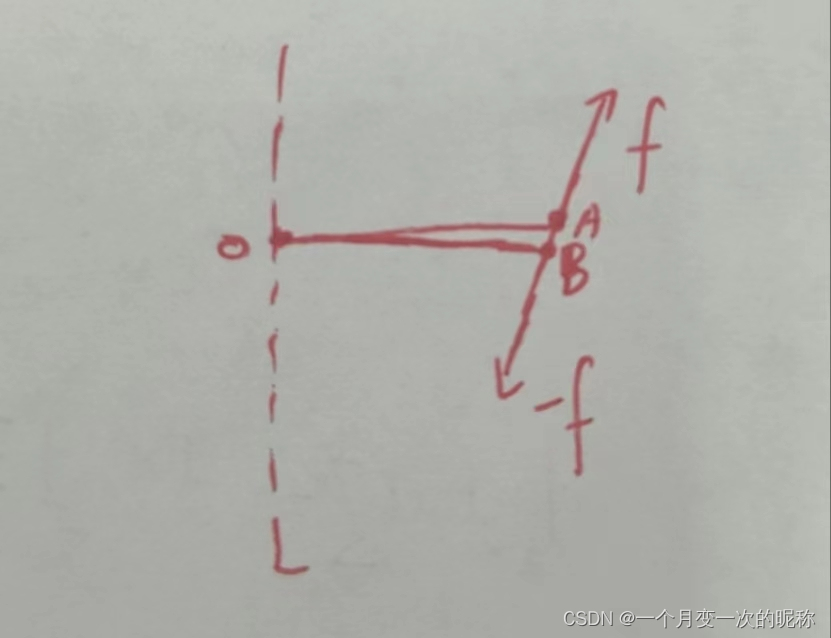
图2

其实不难理解物体所有内力的力矩合为0，我们借图2来研究，有一个力f【微元b给微元a的】，那么必有-f【微元a给b的】，力矩的定义就是力叉乘位置矢量，这对相互作用力等大反向，由于ab这两个微元非常小，所以他们的位置矢量（OA=OB）也是一样的，这是一种正确的近似，在数学里面屡见不鲜。所以这两个力矩之和就是f×r+（-f）×r=0，一对内力如此，便可以明白所有内力力矩之和为0.

所以对整个物体M来说：

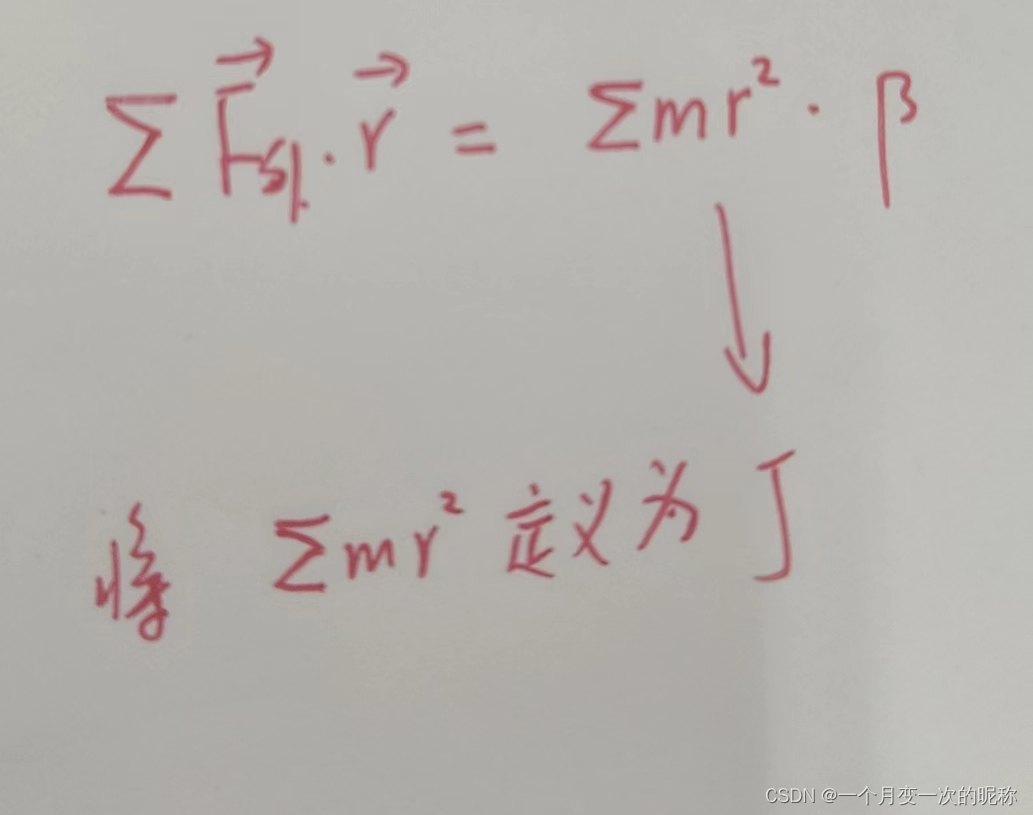
转动公式

定义J=就是转动惯量，显然只与物体质量围绕转轴分布情况有关。

总而言之，定轴转动定律表明，物体所受外力的力矩之和等于该物体的转动惯量J乘以角加速度β。

值得指出的是，在公式推导的过程中的外力F始终都是垂直于转动定轴，因为沿轴的分力对定轴转动无影响，所以在实际应用中，一般都要先把外力分解成垂直于转动定轴的力，这部分的力才有效，。