夜阑卧听风吹雨,铁马冰河入梦来。 —南宋 辛弃疾
🏰代码及环境配置:请参考0.2 环境配置和代码运行 | 动手学运动规划!
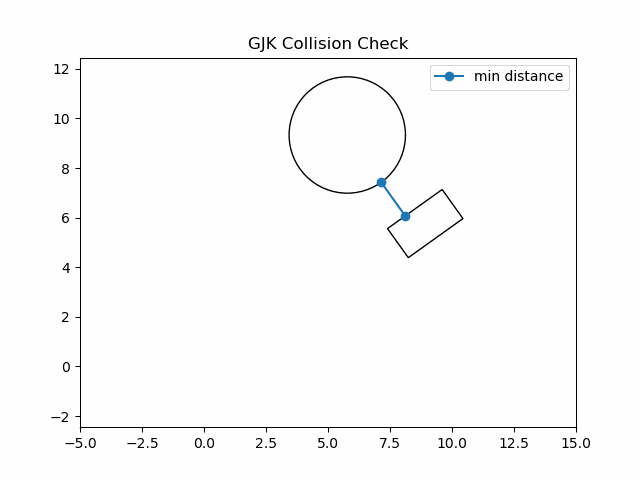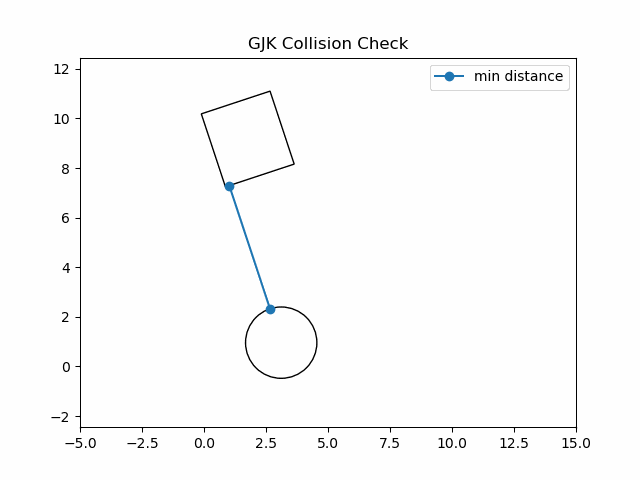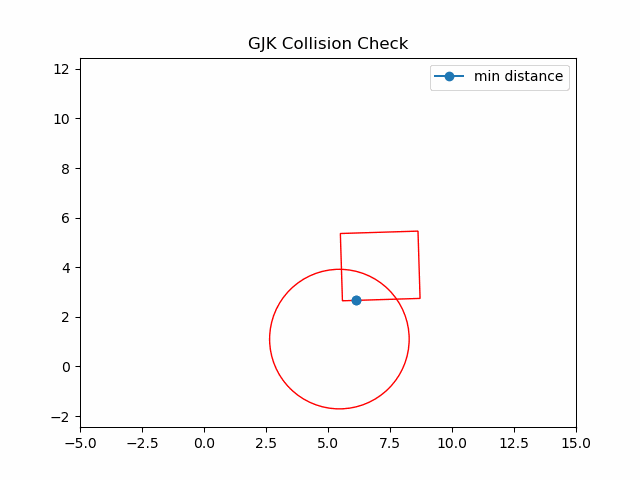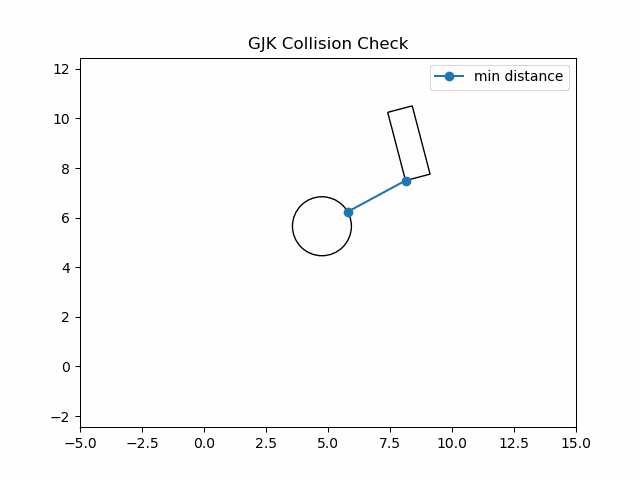
Gilbert–Johnson–Keerthi(GJK)算法,是一种用于检测两个凸集是否重叠的高效算法,并且可以得到两个凸集的最小距离.
1.4.1 GJK算法原理
有两个集合A和集合B,如何确定它们是否相交?
如果存在任何一个点同时属于这两个集合,那么这两个集合就重叠。
另一种表述是,如果存在集合A中点a和集合B中的点b,使得:
a − b = 0 a ∈ A , b ∈ B a-b=0 \\ a \in A, b \in B a−b=0a∈A,b∈B
那么存在交点, 注意这里的0代表原点。
有了这个定义,接下来如何确定这个点是否存在呢?分别暴力遍历A,B中的所有的点显然是可行的,但是效率太低.
1.4.1.1 闵可夫斯基差(Minkowski Difference)
我们可以将A和B两个集合”相减”,会得到一个新的集合: A ⊖ B A \ominus B A⊖B
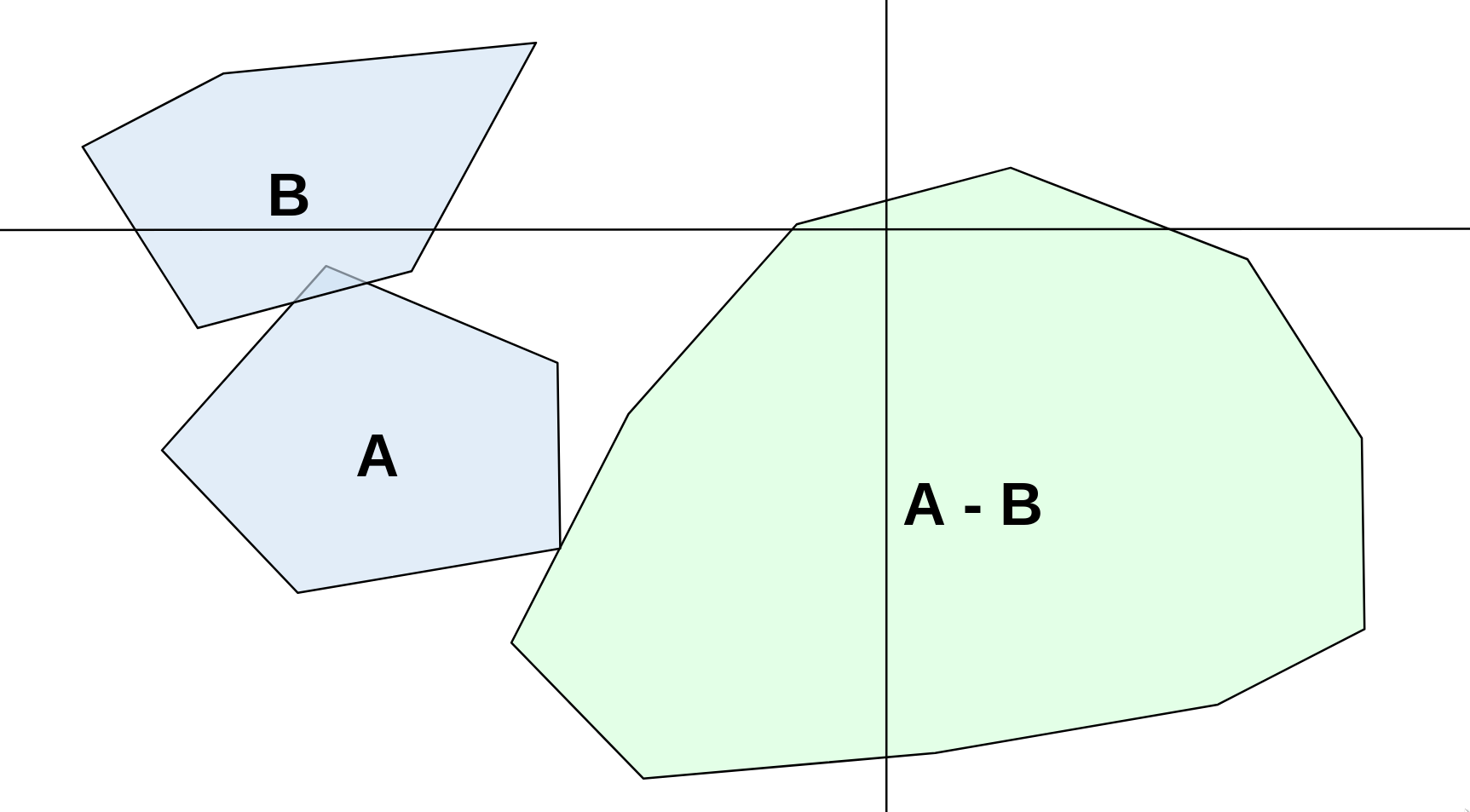
如果 A ⊖ B A \ominus B A⊖B包含原点 O ( 0 , 0 ) O(0,0) O(0,0),也就代表着存在集合A中点a和集合B中的点b,使得 a − b = 0 a-b=0 a−b=0.如下图:
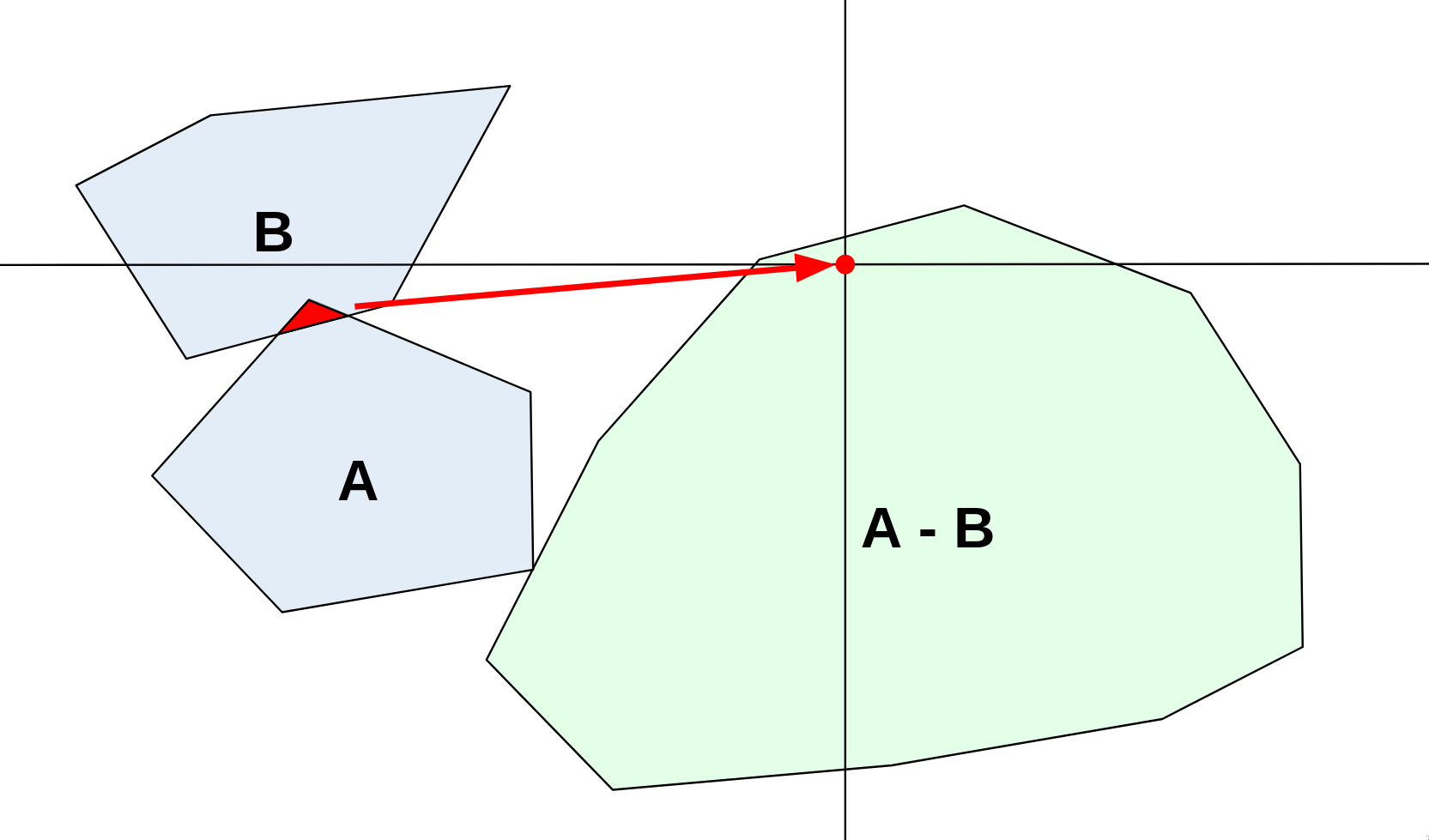
这种结合集合的方式被称为闵可夫斯基差(Minkowski Difference), 更正式地,它被定义为:
A ⊖ B = { a − b ∣ a ∈ A , b ∈ B } A \ominus B=\{a-b \mid a \in A, b \in B\} A⊖B={a−b∣a∈A,b∈B}
这也就是GJK算法的核心内容,寻找两个集合的闵可夫斯基差是否包含原点.
1.4.1.3 凸性
在二维空间中,如果一个凸集包含原点,那意味着我们一定能在边界上找到三个点,组成一个包含原点的三角形.
也就是说:如果A ⊖ B是凸的,那么我们只需要在边界上寻找点,这节省了大量的工作.
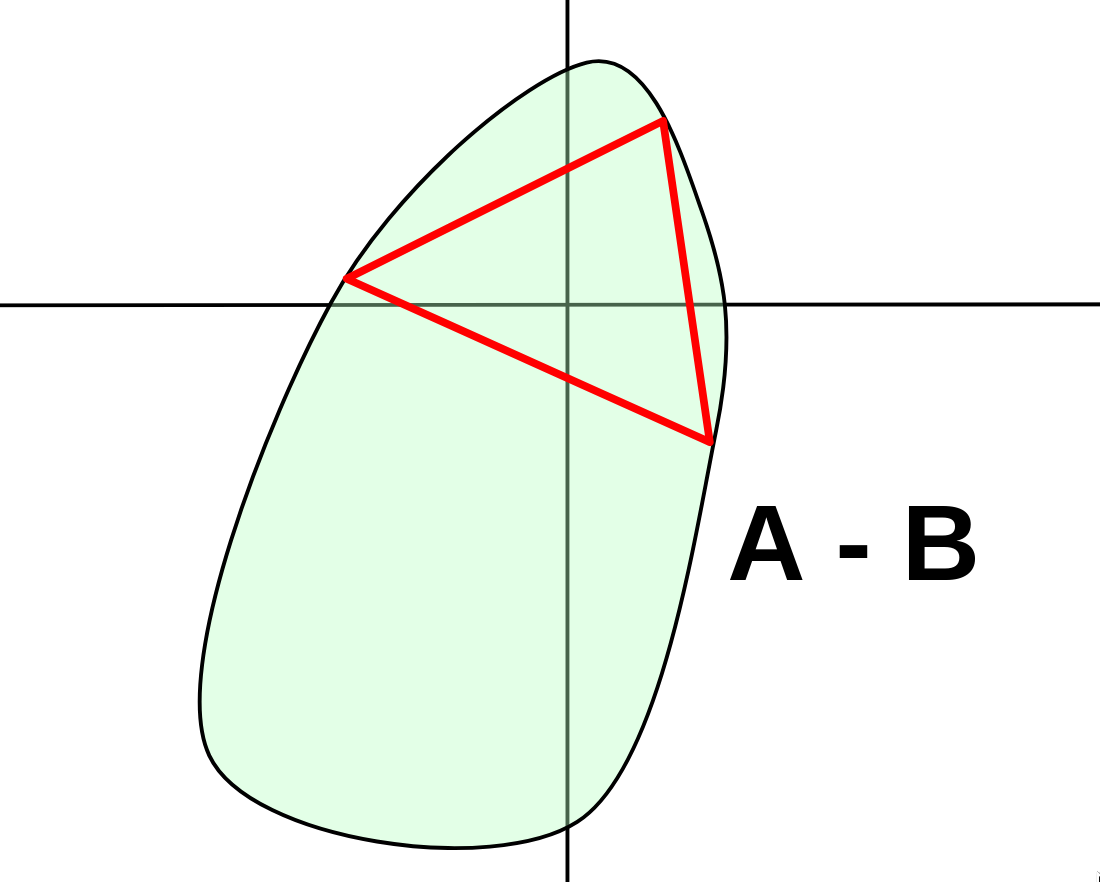
如何确保 A ⊖ B A \ominus B A⊖B是凸集呢?这里给出一个定理:
任何两个凸集的闵可夫斯基差也是凸的。
所以,我们只需要保证A和B是凸集.也就是说,GJK也是一个只能处理凸集之间的碰撞检测算法.
如果需要处理非凸集,比如下图的A和B,是两个非凸集.我们把非凸集分解成凸的子集,然后依次对这些子集执行GJK算法.分解非凸集的方法这里不再赘述.
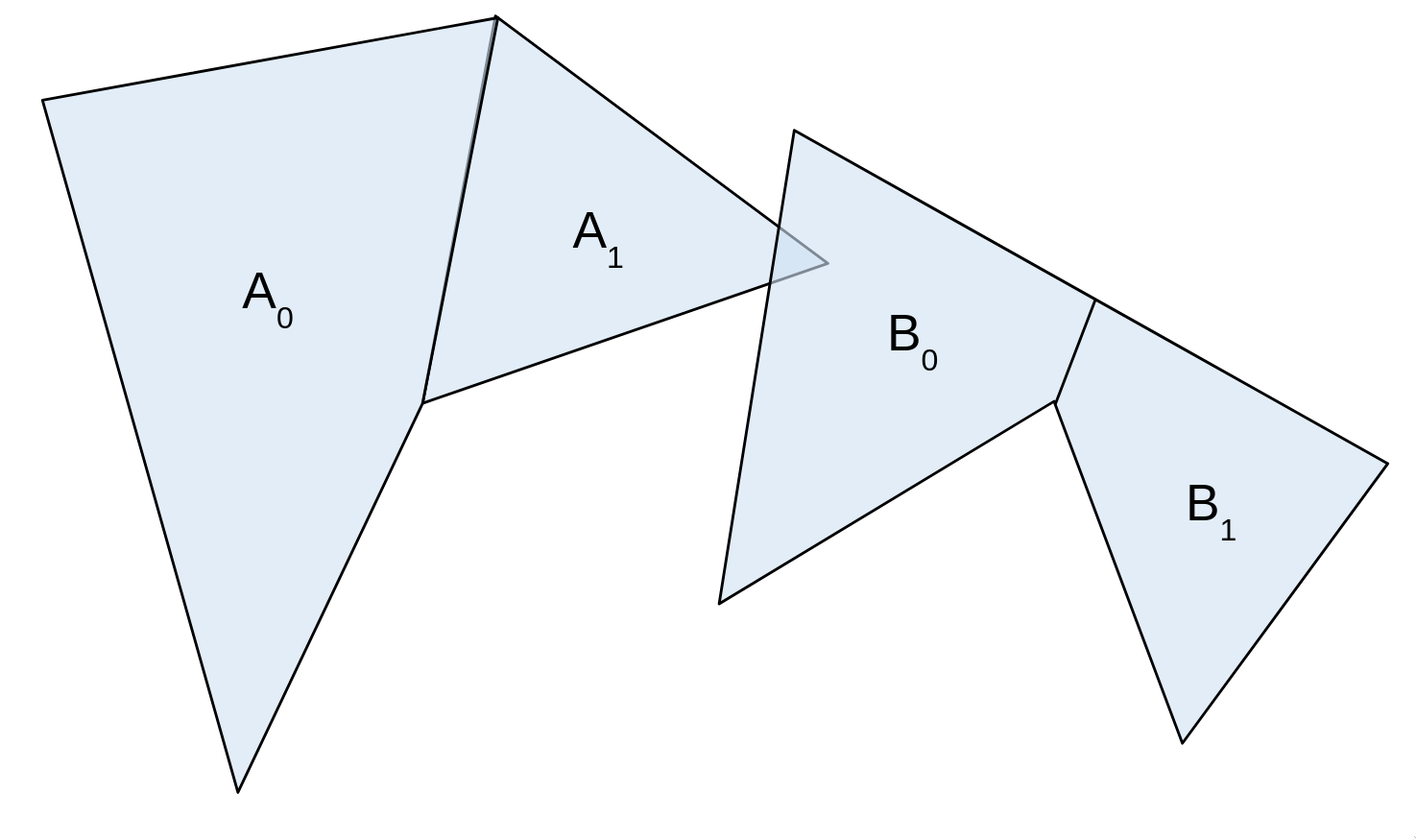
1.4.1.3 单纯形
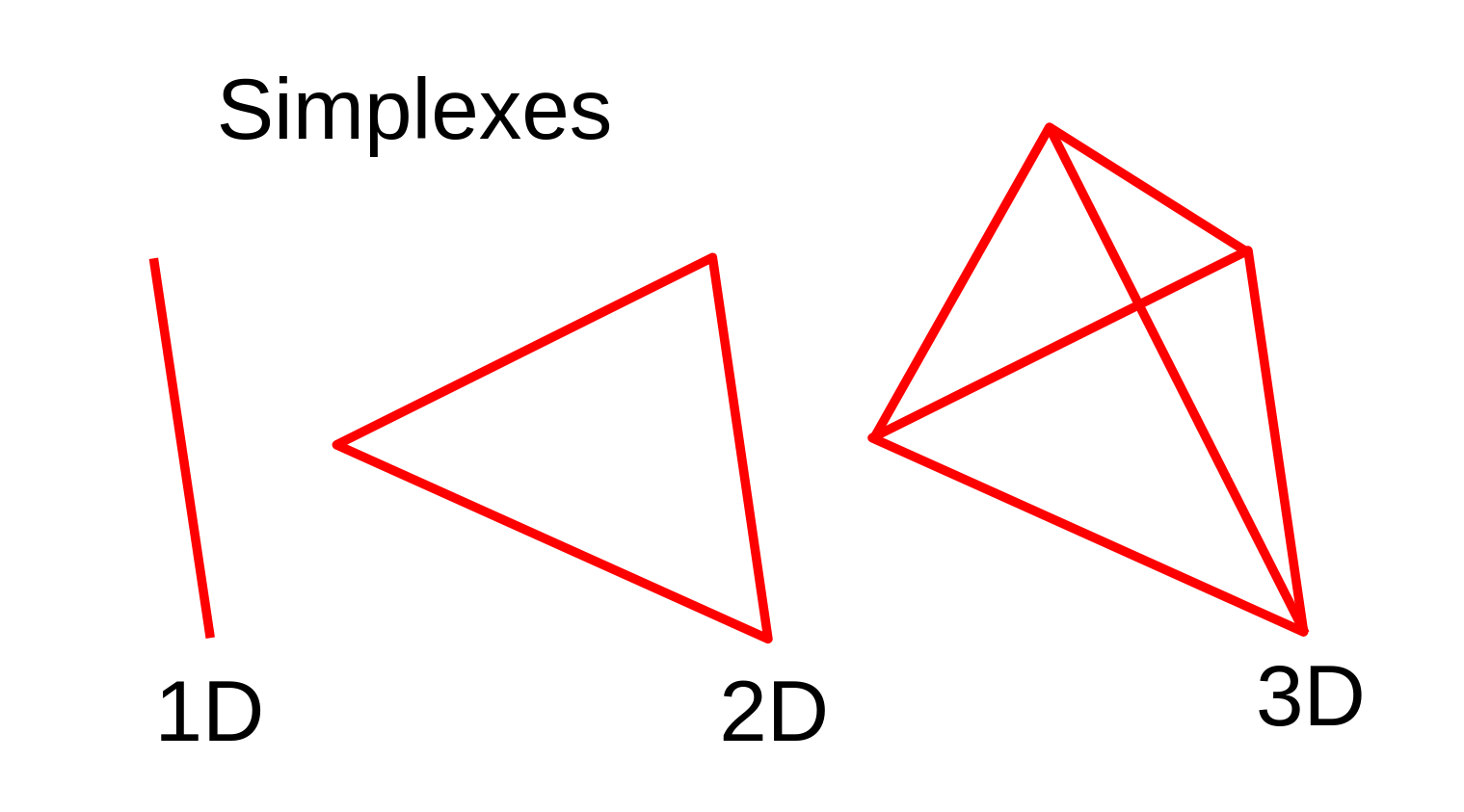
我们正在寻找 A ⊖ B A \ominus B A⊖B中的一个包围原点的三角形。更一般地说,我们正在寻找维度中的一个单纯形。一个n维单纯形就是能够包围一个n维区域的最简单的多面体。例如,一个3D单纯形是一个四面体,因为它有最少的顶点来包围一个体积。
对于规划算法中常见的2维问题,2d单纯形就是一个三角形.
那么问题也就变成了:
- A ⊖ B A \ominus B A⊖B中是否存在包含原点的单纯形。
1.4.1.3 支持函数(Support Function)
很容易想到是:暴力遍历 A ⊖ B A \ominus B A⊖B上所有的顶点,确定是否存在一个单纯形包含原点.
但是能否用尽量少的次数,尽量快的确定:是否存在包含原点的单纯形呢?
为了能够快速的构造包含原点的单纯形,我们设计了支持函数(Support Function),它接受一个向量(方向)作为输入,返回 A ⊖ B A \ominus B A⊖B上相反反向的最远的点来构造新的单纯形.
选择最远的点是为了尽可能的包含更大的面积,尽可能包含原点(如果存在),来减少迭代的次数.
这个过程会在后文详细介绍.
1.4.1.4 点积和叉积
如何确定多边形在d方向上最远的点呢,将多边形上的每一个点与d做点积即可.
- 两个向量的点积结果大小与在向量方向上的投影长度正相关,正负代表方向是否一致.
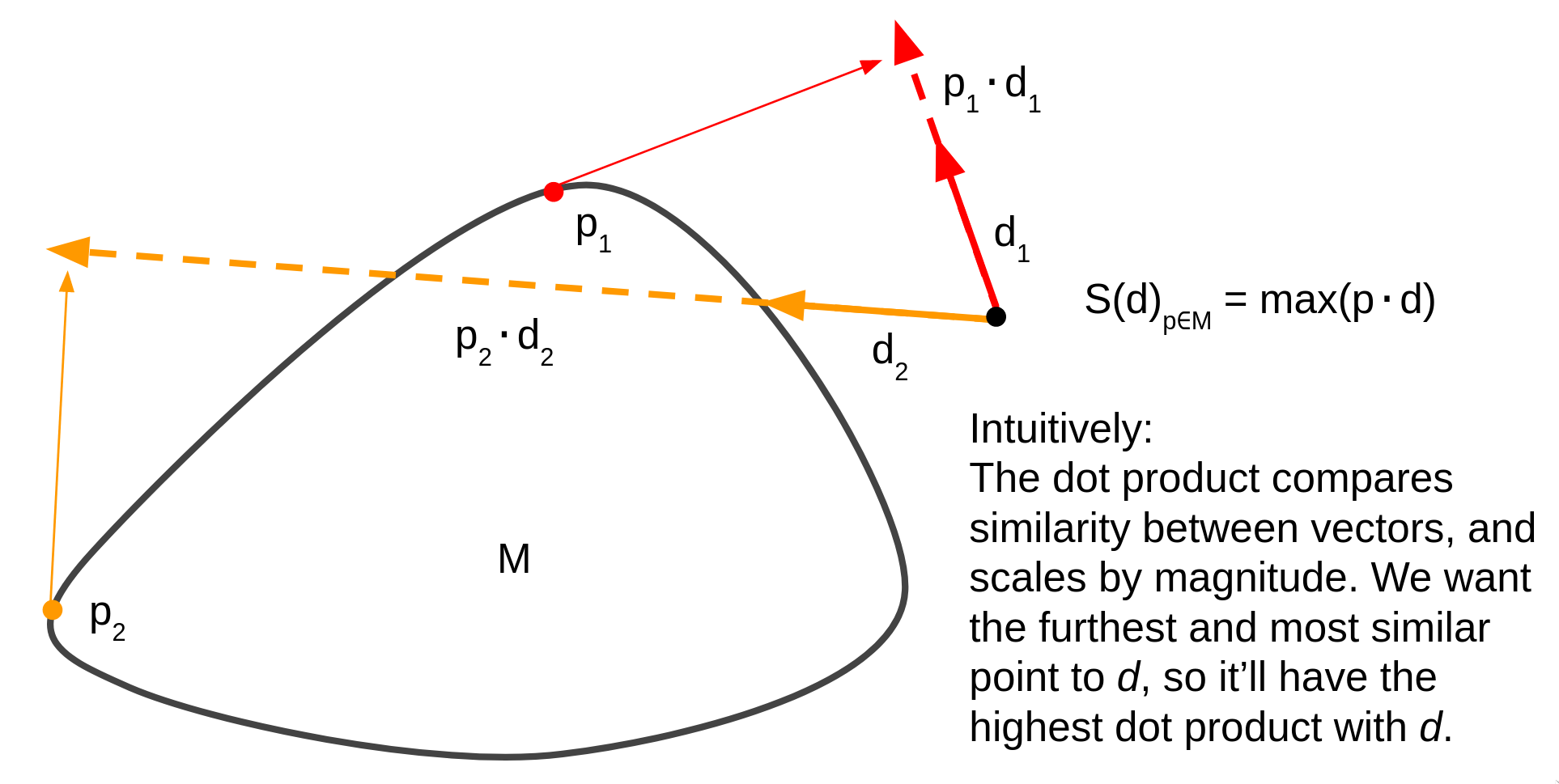
如下图所示,黑点是原点 O O O.
p 1 ⃗ = O P 1 → p 2 ⃗ = O P 2 → \vec{p_1}=\overrightarrow{OP_1} \\ \vec{p_2}=\overrightarrow{OP_2} p1=OP1p2=OP2
边界点中 p 1 ⃗ ⋅ d 1 ⃗ \vec{p_1}\cdot \vec{d_1} p1⋅d1结果最大, 所以 d 1 ⃗ \vec{d_1} d1/方向最远的点是 P 1 P_1 P1.
同理, d 2 ⃗ \vec{d_2} d2方向最远的点是 P 2 P_2 P2.
另外我们还需要知道叉积的几何意义:
- a ⃗ × b ⃗ \vec{a} \times \vec{b} a×b叉乘结果的正负表示: a ⃗ \vec{a} a在 b ⃗ \vec{b} b的右侧还是左侧
1.4.2 GJK算法步骤
我们先给出GJK的算法步骤,在例子中会解释相关逻辑
1.4.2.1 步骤
(1)随机一个初始方向 d ⃗ \vec{d} d,调用Support()函数得到A上最远的点 P a P_a Pa
对方向$\vec{d}$取反,调用Support()函数得到B上最远的点$P_b$
(2) P a − P b P_a- P_b Pa−Pb得到 A ⊖ B A \ominus B A⊖B上的 P p P_p Pp
(2a)如果 d ⃗ ⋅ O P p → > 0 \vec{d} \cdot \overrightarrow{OP_p}>0 d⋅OPp>0,把 P p P_p Pp加入到单纯形中;
(2b)如果 d ⃗ ⋅ O P p → < 0 \vec{d} \cdot \overrightarrow{OP_p}<0 d⋅OPp<0,返回无碰撞.(如果计算最小距离,则不返回)
(3)对 p ⃗ \vec{p} p(也就是 O P p → \overrightarrow{OP_p} OPp)取反,调用Support()函数得到 A ⊖ B A \ominus B A⊖B上的新的 P − p P_{-p} P−p点
(3a)如果 − p → ⋅ O P − p → > 0 \overrightarrow{-p} \cdot \overrightarrow{OP_{-p}}>0 −p⋅OP−p>0,把 P − p P_{-p} P−p加入到单纯形中
(3b)如果 − p → ⋅ O P − p → < 0 \overrightarrow{-p} \cdot \overrightarrow{OP_{-p}}<0 −p⋅OP−p<0,返回无碰撞
循环:
(4)判断单纯形是否包含原点:
(4a)如果包含,则返回碰撞
(4b)如果不包含,单纯形只保留离原点最近的一条边上的两个点
(5)两个点组成的边,将方向 p ⃗ \vec{p} p更新为 边朝向原点方向的垂线.回到步骤(4)继续循环
注意:如果需要得到两个几何之间的最小距离, (2b)可以不直接返回是否碰撞,继续迭代
1.4.2.2 例子
为了能够更明白的解释算法步骤,这里我们举一个例子:
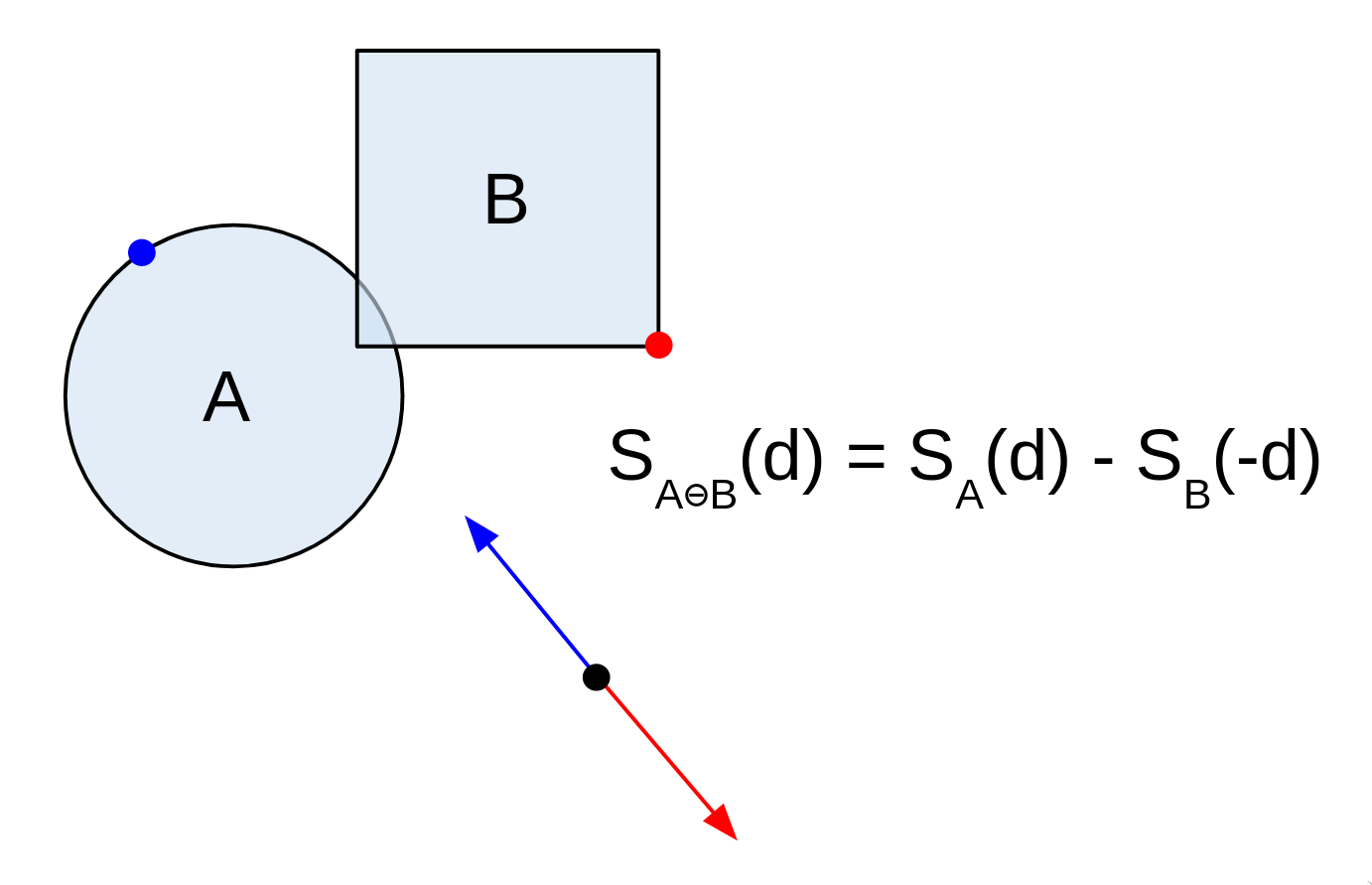
(1)随机一个初始方向方向 d ⃗ \vec{d} d,图中蓝色向量,得到A上的蓝点;对方向 d ⃗ \vec{d} d取反,图中黄色向量,得到B上的红点
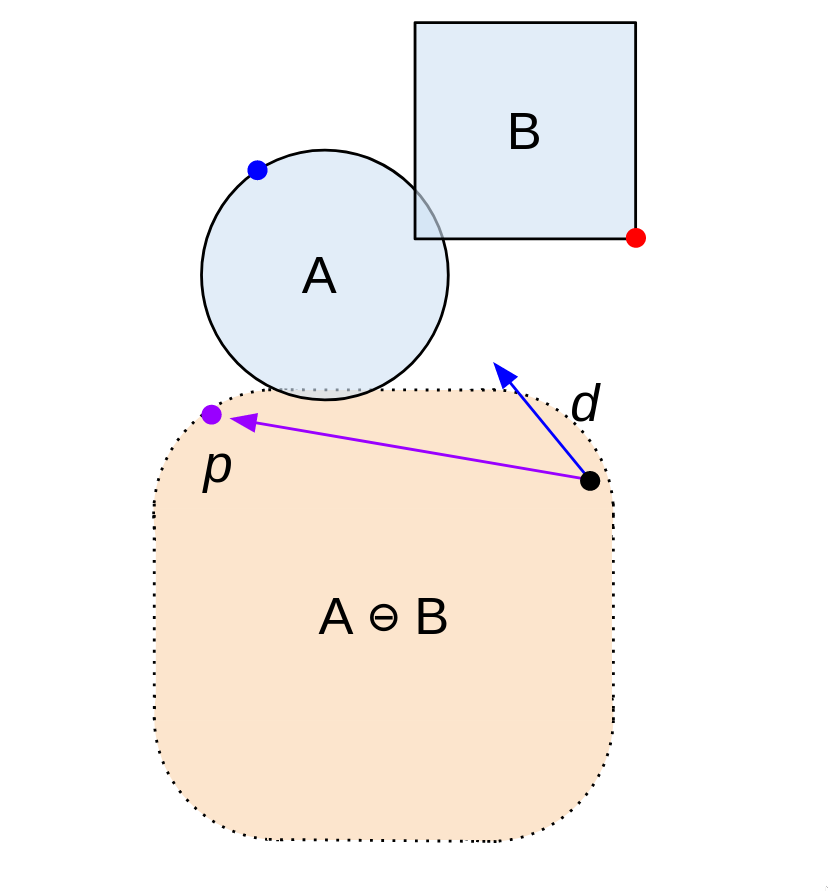
(2) P a − P b P_a- P_b Pa−Pb得到 A ⊖ B A \ominus B A⊖B上的 P p P_p Pp
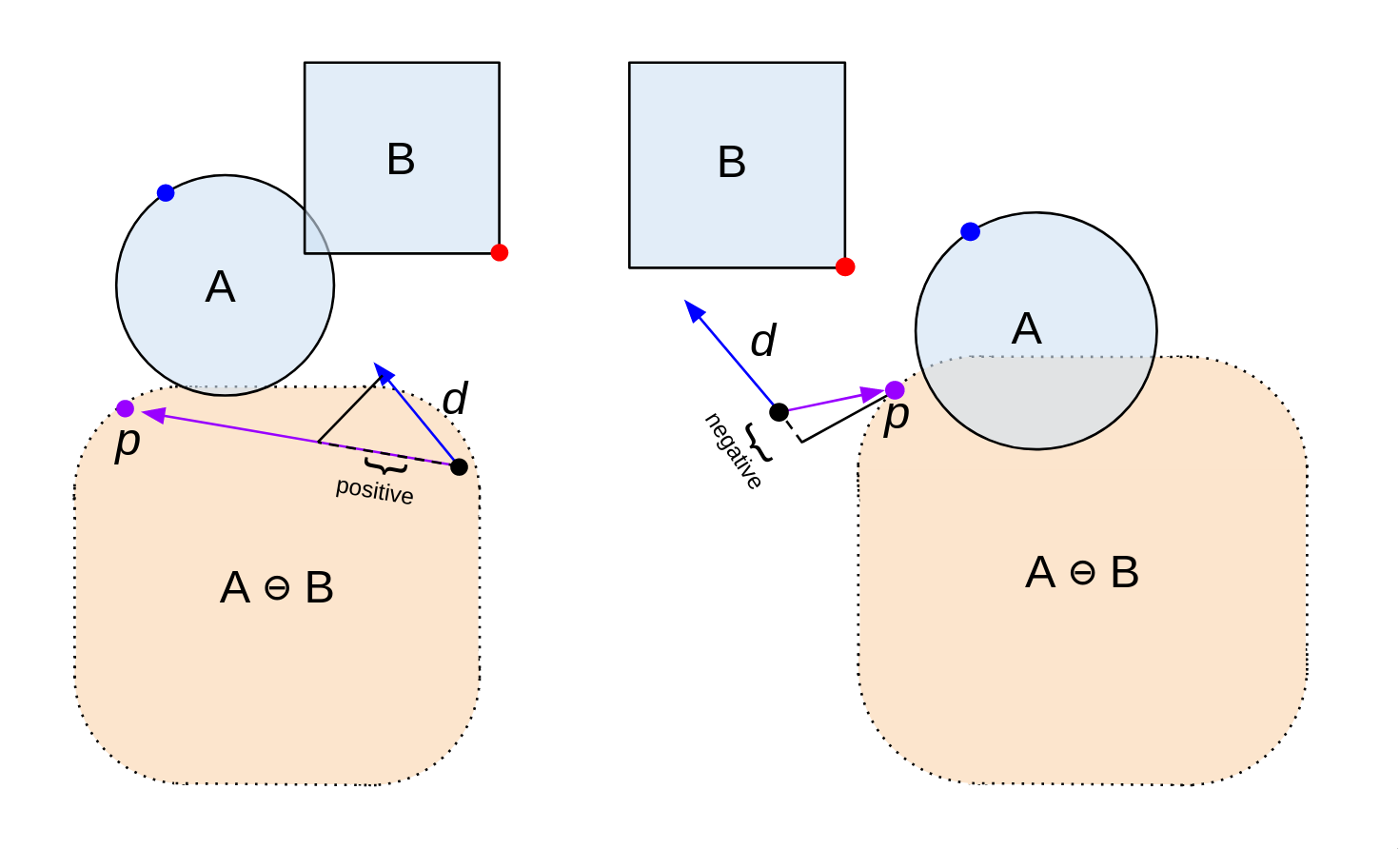
(2a 2b)计算 d ⃗ ⋅ O P p → \vec{d} \cdot \overrightarrow{OP_p} d⋅OPp,判断是否碰撞.
这里给出两个例子,左边点积是正的,代表仍然可能发生碰撞;右边点积结果是付的,代表一定不会碰撞.
**但是为什么可以做这样的判断呢?**我们这里回到没有闵可夫斯基差的视角,直观的解释一下:
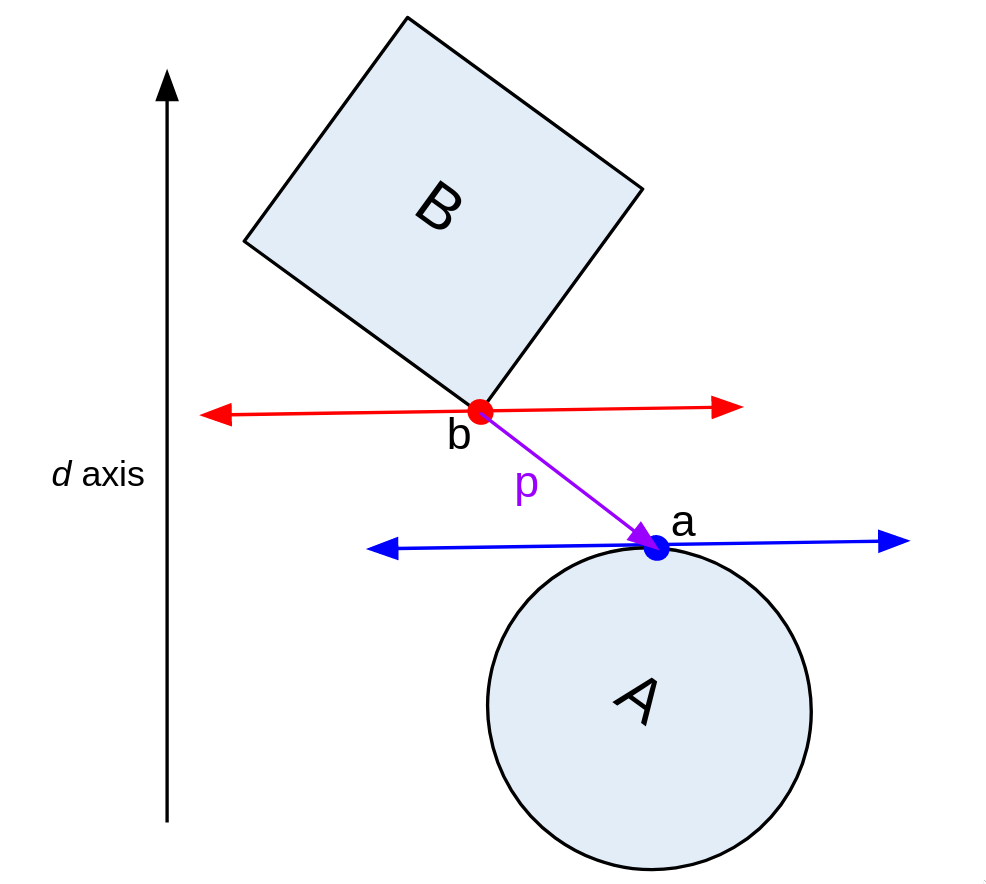
向量 d ⃗ \vec{d} d朝正上方,那么a是A上最上方的点,b是B上 − d ⃗ \vec{-d} −d方向最下方的点.
我们知道 A ⊖ B A \ominus B A⊖B上的点 P p P_p Pp是 P a − P b P_a- P_b Pa−Pb得到的, 同样向量 p ⃗ = a ⃗ − b ⃗ \vec{p}=\vec{a}-\vec{b} p=a−b
那么我们很显然能够看到,如果向量 p ⃗ \vec{p} p和向量 d ⃗ \vec{d} d的方向相反,那么A和B之间一定存在间隙!也就是不会发生碰撞.但是如果方向相同,无法判断一定会发生碰撞.
(3)在 A ⊖ B A \ominus B A⊖B上对 p ⃗ \vec{p} p取反,调用Support()函数得到最远的点 S ( − p ⃗ ) S(\vec{-p}) S(−p)
(3a 3b)计算 − p → ⋅ O S − p → \overrightarrow{-p} \cdot \overrightarrow{OS_{-p}} −p⋅OS−p,
- 如果是正的,代表在 − p → \overrightarrow{-p} −p方向上的最远点 S ( − p ⃗ ) S(\vec{-p}) S(−p),已经跨越了原点,仍然有可能包含原点;
- 如果是负的,代表最远点都没有跨过原点,不可能包含原点了.返回无碰撞
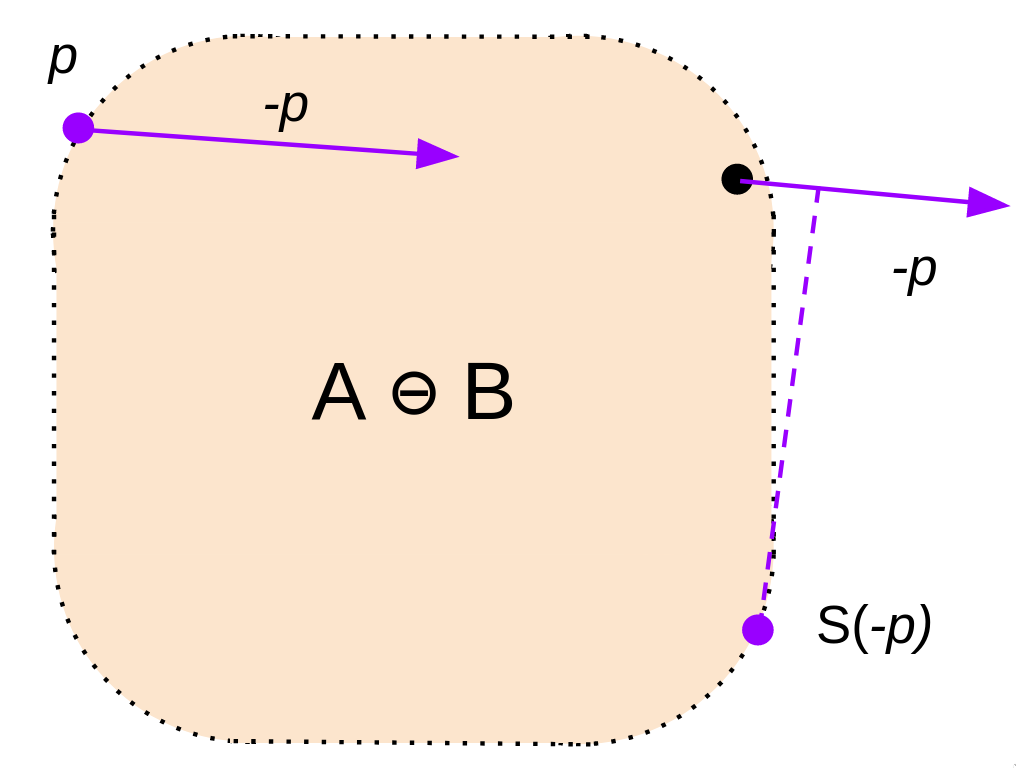
(4)目前单纯形只有 P p P_p Pp和 P − p P_{-p} P−p两个点,跳过
(5)取这两个点组成的边的垂线方向,调用Support()函数,得到新的最远的点
(4)回到步骤(4)
单纯形不包含原点,留下离原点最近的边,也就是右边的这条边
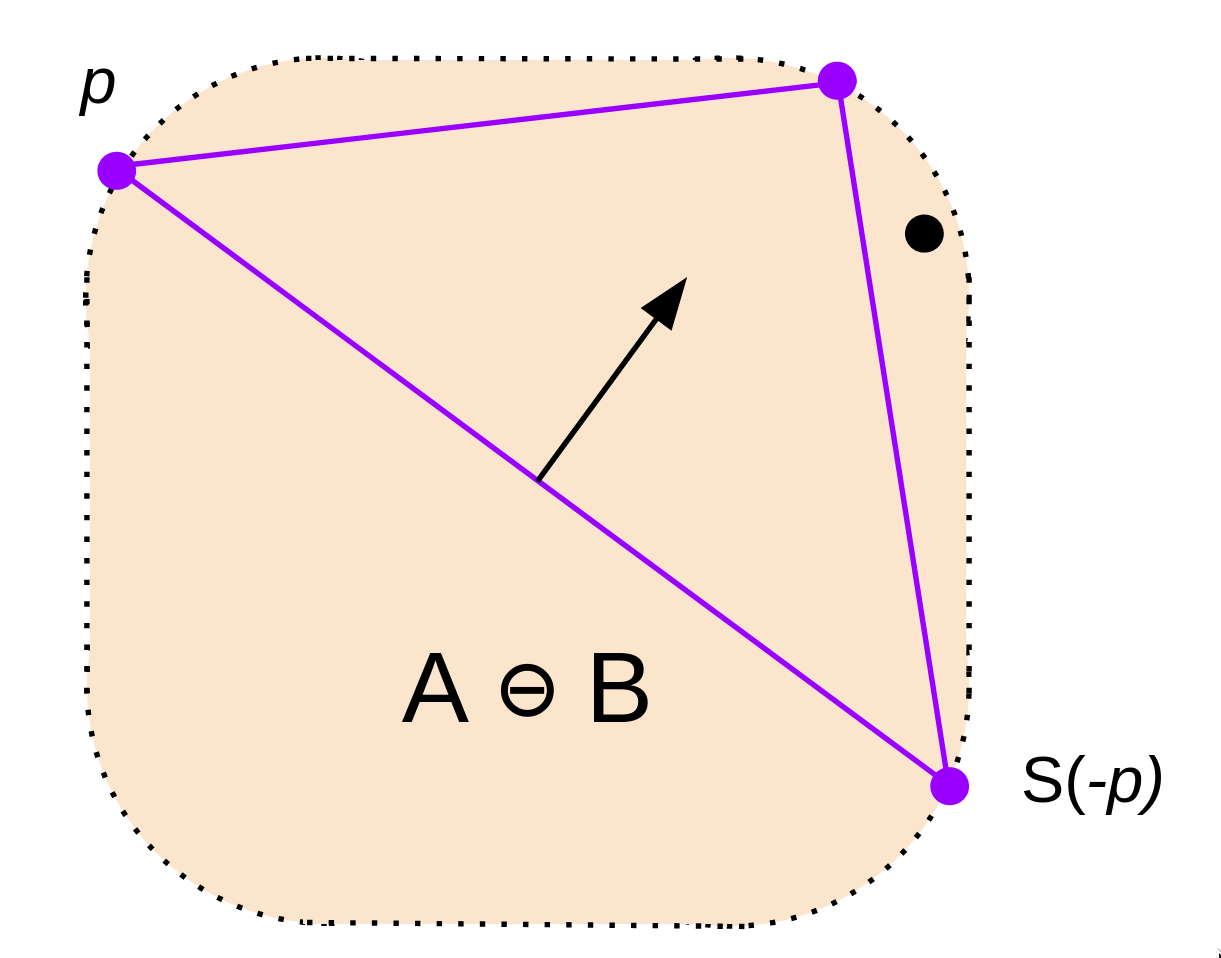
(5)取这两个点组成的边的垂线方向,调用Support()函数,得到新的最远的点,也就是最右边的点
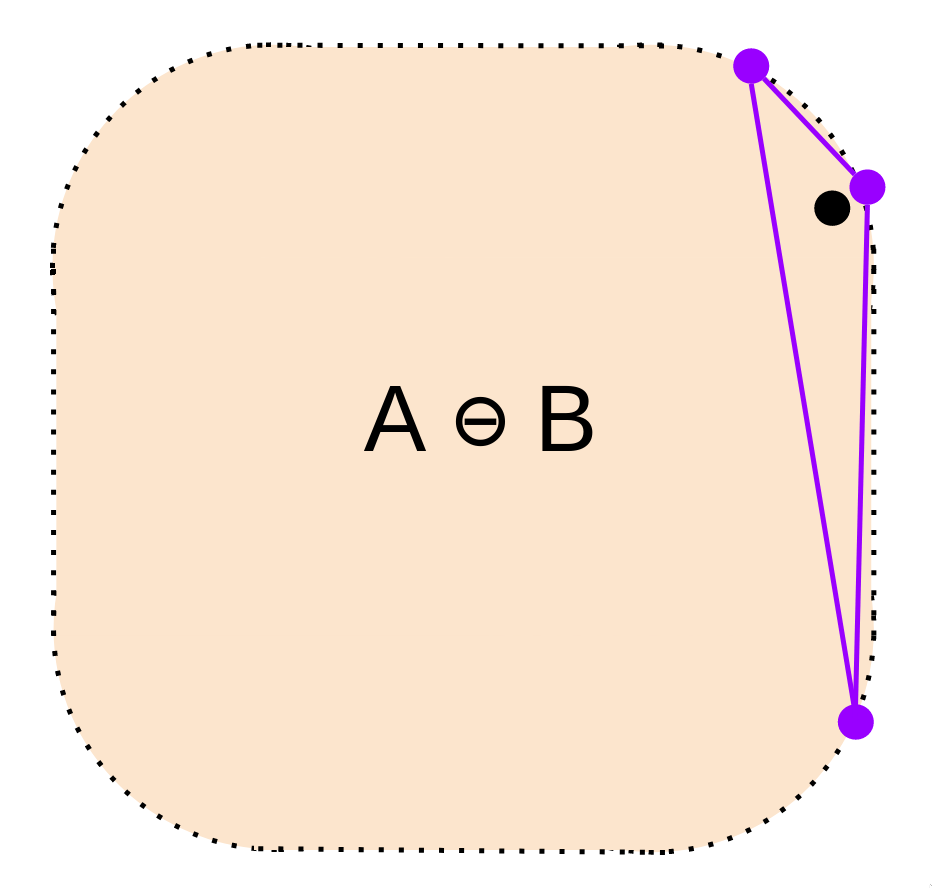
(4)再次回到步骤(4)
终于,单纯形包含了原点,返回碰撞!
下一节, 我们会解析和运行代码.
参考链接:
https://computerwebsite.net/writing/gjk
🏎️自动驾驶小白说官网:https://www.helloxiaobai.cn
🐮GitHub代码仓:https://github.com/Hello-Xiao-Bai/Planning-XiaoBai!
🔥小红书官方店铺:https://www.xiaohongshu.com/vendor/66e3ea57741c6300157a9103
🌠代码配合官网教程食用更佳!
🚀知乎,微信,知识星球全平台同号!






















 2677
2677

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








