概览
关于自动驾驶车道线拟合算法,常用的方法有B样条、三次样条插值、Ransac、最小二乘法等等。
但是针对于高精度地图的车道线拟合,由于车道线坐标点已知,所以不需要有控制点进行约束,那么B样条、贝塞尔曲线等都不太适合;三次样条插值曲线每两个坐标点都拟合一组参数,如果高精度地图为20cm一个点的画,那么100m的道路一条车道线就将有500组参数,对于性能是不乐观的;而Ransac更适用于散点拟合,对于已知的有序点再进行多次迭代也是耗费性能的,所以目前还是以最小二乘法为主流方案。
最小二乘法,又称最小平方法,其实就是深度学习中的均方误差。它通过最小化 误差的平方和 寻找数据的最佳函数匹配。主要作用是从一堆相关数据中求解数据的一般性规律。在图像处理方面多用于各种形状的拟合。
最小二乘拟合直线,主要体现为找到一条直线,使得所有已知的点到这条直线的欧式距离的和最小(或者理解为点到直线的误差平方和最小)。开始之前先引入一个误差的概念。已知直线y=2x。现有点(x1,y1),求误差是多少,答案就是y1 - 2 * x1。
具体使用哪种模型,还是要根据系统的实际需求:
- 有时要求高速的车道线输出,曲率变化小,那用简单的线性模型就好;
- 有些需要精确地道路模型,那就要求三次曲线或二次曲线;
- 有些是视觉车到模型,那就要考虑引用Ransac或者Catmull_Rom样条曲线。
总之,在做算法工作时,没有最好的算法,只有最适合的算法。
车道线的数学模型相关知识点 可阅读 blog
拟合线性方程
曲线拟合中最基本和最常用的是直线拟合。设x和y之间的函数关系为:
y=a+bx
此处a 对应车道线里的 lateral deviation横向偏移;
斜率b 对应车道线里的 heading angle车辆航向角 ;
车辆航向角定义
式中有两个待定参数,a代表截距,b代表斜率。对于等精度测量所得到的N组数据(xi,yi),i=1,2……,N。xi值被认为是准确的,所有的误差只联系着yi。下面利用最小二乘法把观测数据拟合为直线。
用最小二乘法估计参数时,要求观测值yi的偏差的加权平方和为最小。对于等精度观测值的直线拟合来说,可使下式的值最小:
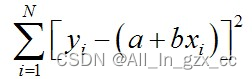
上式分别对a、b求偏导得:

整理后得到方程组:
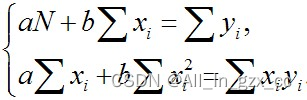
解上述方程组便可求得直线参数a和b的最佳估计值:
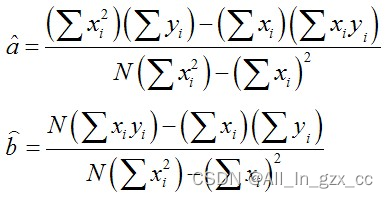
相关系数r:
最小二乘法处理数据除给出a、b外,常常还给出相关系数r, r定义为:
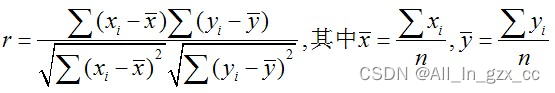

或者 有的公式 除以了 n:

- 当r>0时,斜率 = X的标准差 / Y的标准差;
- 当r<0时,斜率 = -X的标准差 / Y的标准差;
通常用SD线来直观的表示数据的走向:
1)当r<0时,SD线的斜率小于0时,则说明数据负相关,即当x增大时y减少。
2)当r>0时,SD线的斜率大于0时,则说明数据正相关,此时当x增大时y增大。
3)相关系数r的范围在[-1,1]之间,当r=0时表示数据相关系数为0(不相关)。当r=正负1时,表示数据负相关,此(x,y)点数据都在SD线上。
4)r的值越接近正负1说明(x,y)越靠拢SD线,说明数据相关性越强,r的值越接近0说明(x,y)点到SD线的散度越大(越分散),数据相关性越小。
代码实现
void LineFitLeastSquares(float *data_x, float *data_y, int data_n)
{
float A = 0.0;
float B = 0.0;
float C = 0.0;
float D = 0.0;
float E = 0.0;
float F = 0.0;
for (int i=0; i<data_n; i++)
{
A += data_x[i] * data_x[i];
B += data_x[i];
C += data_x[i] * data_y[i];
D += data_y[i];
}
// 计算斜率a和截距b
float a, b, temp = 0;
if( temp = (data_n*A - B*B) )// 判断分母不为0
{
a = (data_n*C - B*D) / temp;
b = (A*D - B*C) / temp;
}
else
{
a = 1;
b = 0;
}
// 计算相关系数r
float Xmean, Ymean;
Xmean = B / data_n;
Ymean = D / data_n;
float tempSumXX = 0.0, tempSumYY = 0.0;
for (int i=0; i<data_n; i++)
{
tempSumXX += (data_x[i] - Xmean) * (data_x[i] - Xmean);
tempSumYY += (data_y[i] - Ymean) * (data_y[i] - Ymean);
E += (data_x[i] - Xmean) * (data_y[i] - Ymean);
}
F = sqrt(tempSumXX) * sqrt(tempSumYY);
float r;
r = E / F;
}
拟合一元三次方程(高阶方程)
目前的主流方法直接用最小二乘法做三次曲线拟合,但本文以引入为主,上面先以线性最小二乘法引入。 y = ax + b
使残差和最小:
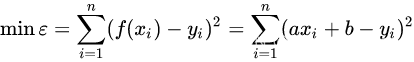
在自动驾驶中,需要的就是将曲线参数传入控制规划端用以描述道路形状,现阶段主流的拟合方程为一元三次方程,例如MobileEye以C0,C1,C2,C3传出,所以在我们目前的工作中,要做的就是针对点集数据,求出最优参数使得残差最小。由于残差和的表达式是二元函数,因此分别对参数 a, b 求偏导,使其等于0时,得到残差和的最小值:
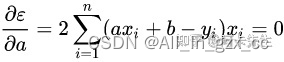

整理后得
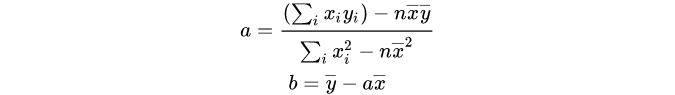
在一次函数的情况下,函数拟合需要计算两个未知量。推广到高阶函数,就需要一个统一公式去做相关运算。
在高阶函数下:
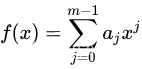
同理我们还是有 n 个自变量
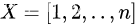
和观测值
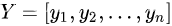
不妨将上式写成矩阵形式。

上述矩阵方程记为:
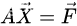
观测值 Y 写为向量的形式,记为:
同样,使得残差的平方和最小: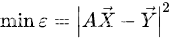
将上式右半部展开,得:

根据矩阵转置相乘的转换关系,可得: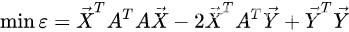
化简为: 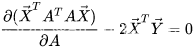
根据矩阵的求导法则:
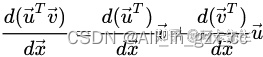
即:
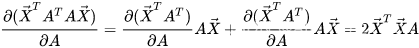
因此 残差平方和 对 各阶系数 的偏导为:
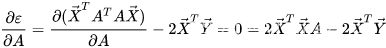
化简后,我们得到高阶函数各项系数的最优取值: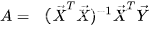
面对线性数学模型,参数矩阵较大时,求逆矩阵的耗时较大,上式的直接求逆可能就略显鸡肋,一般需要通过QR分解、Cholesky分解、SVD分解进行求解。
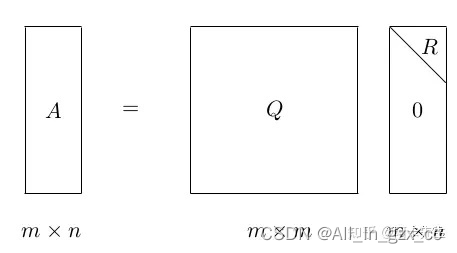
面对非线性数学模型,无法直接写出导数或者导数过于复杂,也无法用上述矩阵分解的方式求解,所以一般会请来我们认识的雅克比、海塞来求解,目前主流的方法为:最速下降法、牛顿法、高斯牛顿法、LM等等进行迭代求解,也可以依赖ceres库、G2O库进行求解,后面也会依次介绍。
代码实现
#include <iostream>
#include <Eigen/src/Cholesky/LDLT.h>
Eigen::VectorXd Ls(std::vector<double>& x,std::vector<double>&y)
{
Eigen::Map<Eigen::VectorXd> sampleX(x.data(), static_cast<long>(x.size()));
Eigen::Map<Eigen::VectorXd> sampleY(y.data(), static_cast<long>(y.size()));
Eigen::MatrixXd mtxVandermonde(x.size(), 4);
Eigen::VectorXd colVandermonde = sampleX;
for (int ii = 0; ii < 4; ++ii)
{
if (0 == ii) {
mtxVandermonde.col(0) = Eigen::VectorXd::Constant(static_cast<long>(x.size()), 1, 1);
continue;
}
if (1 == ii) {
mtxVandermonde.col(1) = colVandermonde;
continue;
}
colVandermonde = colVandermonde.array() * sampleX.array();
mtxVandermonde.col(ii) = colVandermonde;
}
Eigen::VectorXd result =(mtxVandermonde.transpose() * mtxVandermonde).inverse() * (mtxVandermonde.transpose()) * sampleY;
return result;
}//代码原文参见
https://zhuanlan.zhihu.com/p/268884807
输出结果后,就得到了数据点拟合曲线的相关参数,即可表达当前道路形状,用于后端控制。
参考链接:
https://guyuehome.com/35243
https://blog.csdn.net/qq_36251561/article/details/88020558
https://blog.csdn.net/Naruto_ahu/article/details/8694366

























 2927
2927











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








