多元函数变限积分求导问题


隐函数问题
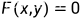
研究什么条件下才能确定隐函数
隐函数的连续性和可微性
隐函数存在性条件
若
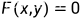 能确定隐函数,则存在
能确定隐函数,则存在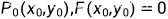
若要求
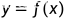 可微,由链式法则得:
可微,由链式法则得:

隐函数存在唯一性定理
若满足下列条件:
(1)函数 在以
在以 为内点得某一区域
为内点得某一区域 上连续
上连续
(2)
(3)在 内存在连续的对y的偏导数
内存在连续的对y的偏导数
(4)
则在点 的某领域
的某领域 内,方程
内,方程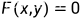 唯一地确定
唯一地确定
定义在某区间 内的(隐)函数
内的(隐)函数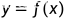 ,使得
,使得
(1)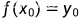 ,当
,当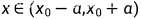 时,
时, 且
且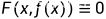
(2) 在
在 内连续
内连续
隐函数可微性定理
函数 满足隐函数存在唯一性定理,并在
满足隐函数存在唯一性定理,并在 上存在连续的对x的偏导数,则函数
上存在连续的对x的偏导数,则函数 确定的隐函数
确定的隐函数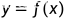 在其定义域
在其定义域 内有连续导函数且
内有连续导函数且
多元函数隐函数问题
若满足下列条件:
(1)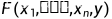 在以
在以 为内点的区域
为内点的区域 上连续
上连续
(2)
(3)偏导数 在D内存在且连续
在D内存在且连续
(4)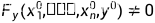
则在点  的某邻域
的某邻域  内,方程
内,方程  唯一地确定了一个定义在
唯一地确定了一个定义在 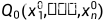 的某邻域
的某邻域  内的 n 元连续函数(隐函数)
内的 n 元连续函数(隐函数)  使得
使得
类似的 不写了
y在U(Q_0)内有连续偏导数


























 520
520

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










