决策规划算法二：生成参考线（FEM_POS_DEVIATION_SMOOTHING）

肥嘟嘟的左卫门

已于 2022-05-07 22:01:22 修改

阅读量1.8k

点赞数 6

文章标签：参考线离散点平滑 QP

于 2022-05-07 16:17:48 首次发布

本文链接：https://blog.csdn.net/ChenGuiGan/article/details/124633387

版权

Apollo的的规划算法基于Frenet坐标系，因此道路中心线的平滑性控制着车辆是否左右频繁晃动，而高精地图的道路中心线往往不够平滑。

离散点平滑法，包括

1，FEM_POS_DEVIATION_SMOOTHING有限元位置差异

2，COS_THETA_SMOOTHING余弦）

3，QpSplineReferenceLineSmoother（三次样条插值法）

4，SpiralReferenceLineSmoother（螺旋曲线法）

本文只讲解FEM_POS_DEVIATION_SMOOTHING有限元位置差异的方法。

一，为什么需要重新生成参考线

导航路径存在的问题：1，导航路径过长；2，不平滑

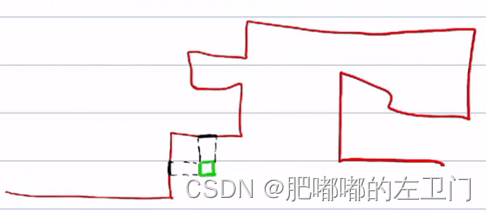
导致的结果：

1，不利于主车以及障碍物寻找投影点，甚至出现多个投影点。

2，原本的导航路径不平滑，车辆无法直接进行轨迹跟踪。

解决方案：根据导航路径，生成参考线。

二，生成参考线的具体步骤与方法

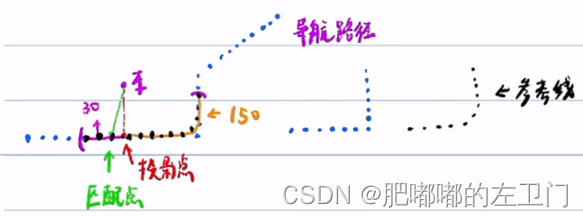
1，找到匹配点以及投影点

2，以匹配点或者投影点为原点，往后取30个点，往前取150个点。对这180个点进行平滑处理，生成符合要求的参考线，作为该规划周期内的参考线，并以此参考线为Frenet坐标系。

三，参考线平滑方法：QP

方法步骤：

1，设计Cost:平滑程度，与原路径的偏离程度，路径点距离分布的均匀程度。

2，整理Cost目标函数，使其符合QP的表达形式。

$minJ=\frac{1}{2}x^{T}Qx+f^{T}x$

3，考虑约束条件，并整理为QP的约束表达式形式。

$sb: Ax<= b$

4，运用合适的QP求解器进行求解，获取优化后的结果。

四，设计Cost：平滑程度，与原路径的偏离程度，路径点距离分布的均匀程度（长度代价）

1，平滑程度

衡量指标： $\left | P_{1}P_{3} \right |$ 。其值越小，路径越平滑。

2，与原路径的偏离程度

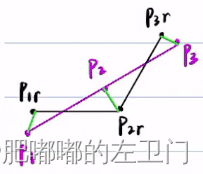
如上图所示，平滑前的点记为 $P_{1r},P_{2r},P_{3r}$ ,平滑后的点记为 $P_{1},P_{2},P_{3}$ 。

虽然路径平滑了，但与原路径距离偏差太大，不符合要求。

衡量指标： $\left | P_{1} P_{1r} \right |+\left | P_{2} P_{2r} \right |+\left | P_{3} P_{3r} \right |$

3,路径点距离分布的均匀程度（长度代价）

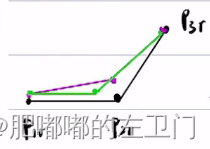
衡量指标： $\left | P_{1} P_{2} \right |^{2}+\left | P_{2} P_{3} \right |^{2}$ 。其值越小，分布越均匀。

五，实例讲解

1，以3个点为例求解目标函数

如上图所示，已知变量：原路径点为： $P_{1r}(x_{1r},,y_{1r}),P_{2r}(x_{2r},,y_{2r}),P_{3r}(x_{3r},y_{3r})$ ，未知变量：优化后的路径点为： $P_{1}(x_{1},,y_{1}),P_{2}(x_{2},,y_{2}),P_{3}(x_{3},y_{3})$ ，求优化后的路径点坐标。

$minJ = (x_{1}+x_{3}-2x_{2})^{2}+(y_{1}+y_{3}-2y_{2})^{2} + \sum_{i =1}^{3}((x_{i}-x_{ir})^{2}+(y_{i}-y_{ir})^{2}) + \sum_{i=1}^{3}((x_{i+1}-x_{i})^{2}+(y_{i+1}-y_{i})^{2})$

2，二次规划的一般形式

$minJ=\frac{1}{2}x^{T}Hx+f^{T}x$

$st:Ax <= b, lb <= x <= ub$

3,n个点的代价函数求解（重点）：

平滑性代价：

$j_{1}=\sum_{i=1}^{n-2}((x_{i}+x_{i+2}-2x_{i+1})^{2}+(y_{i}+y_{i+2}-2y_{i+1})^{2}) =$

$((x_{1}+x_{3}-2x_{2})^{2}+(y_{1}+y_{3}-2y_{2})^{2}+(x_{2}+x_{4}-2x_{3})^{2}+(y_{2}+y_{4}-2y_{3})^{2}+...) =$

$((x_{1}+x_{3}-2x_{2}),(y_{1}+y_{3}-2y_{2}),(x_{2}+x_{4}-2x_{3}),(y_{2}+y_{4}-2y_{3}),...)*((x_{1}+x_{3}-2x_{2}),(y_{1}+y_{3}-2y_{2}),(x_{2}+x_{4}-2x_{3}),(y_{2}+y_{4}-2y_{3}),...) ^{T}$

其中：

$((x_{1}+x_{3}-2x_{2}),(y_{1}+y_{3}-2y_{2}),(x_{2}+x_{4}-2x_{3}),(y_{2}+y_{4}-2y_{3}),...)=$

令 $x^{T}=(x_{1},y_{1},x_{2},y_{2}...)_{1*2n}$

则 $j_{1}=x^{T}A_{1}^{T}A_{1}x$

均匀性代价（长度代价）：

$j_{2}=\sum_{i=1}^{n-1}((x_{i}-x_{i+1})^{2}+(y_{i}-y_{i+1})^{2}) =$

$(x_{1}-x_{2},x_{1}-x_{2},x_{1}-x_{2},x_{1}-x_{2}..)*(x_{1}-x_{2},x_{1}-x_{2},x_{1}-x_{2},x_{1}-x_{2}..)^{T} =$

$(x_{1}-x_{2},x_{1}-x_{2},x_{1}-x_{2},x_{1}-x_{2}..)*(x_{1}-x_{2},x_{1}-x_{2},x_{1}-x_{2},x_{1}-x_{2}..)^{T}$

其中， $(x_{1}-x_{2},x_{1}-x_{2},x_{1}-x_{2},x_{1}-x_{2}..) =$

令 $x^{T}=(x_{1},y_{1},x_{2},y_{2}...)_{1*2n}$

则 $j_{2}=x^{T}A_{2}^{T}A_{2}x$

与原路径的距离偏差代价：

$j_{3}=\sum_{i=1}^{n}((x_{i}-x_{ir})^{2}+(y_{i}-y_{ir})^{2}) =$

$\sum_{i=1}^{n}(x_{i}^{2}+y_{i}^{2})-2\sum_{i=1}^{n}(x_{i}x_{ir}+y_{i}y_{ir})+\sum_{i=1}^{n}(x_{ir}^{2}+y_{ir}^{2})$

由于 $\sum_{i=1}^{n}(x_{ir}^{2}+y_{ir}^{2})$ 是常数，对目标函数的变化没有影响，故可以删除，以简化表达。

令 $x^{T}=(x_{1},y_{1},x_{2},y_{2}...)_{1*2n}$ ， $h^{T}=(x_{1r},y_{1r},x_{2r},y_{2r}...)_{1*2n}$

则： $j_{3}=x^{T}x-2f^{T}x$

综述所述：

$J=j_{1}+j_{2}+j_{3}=\omega _{1}x^{T}A_{1}^{T}A_{1}x+\omega _{2}x^{T}A_{2}^{T}A_{2}x+\omega _{3}x^{T}x-2h^{T}x =$

$x^{T}(\omega _{1}A_{1}^{T}A_{1}+\omega _{2}A_{2}^{T}A_{2}+\omega _{3}E)x-2h^{T}x$

一般情况下，平滑的权重系数远远大于其他2项的权重系数

二次规划的标准形式为：

$J=\frac{1}{2}x^{T}Hx+f^{T}x$

则 $H=2(\omega _{1}A_{1}^{T}A_{1}+\omega _{2}A_{2}^{T}A_{2}+\omega _{3}E)$

$f=-2h$

求解约束条件：

$lb<=\left | x-x_{r} \right |<=ub$

$lb+x_{r}<=x<=ub+x_{r}$

至此，参考线平滑问题转化为二次规划的标准形式，采用成熟的求解器求解即可获得 $x$ ,从而实现导航轨迹的平滑，获得符合要求的参考线轨迹点。


import osqp
import numpy as np
import matplotlib.pyplot as plt
from scipy import sparse

#计算kappa用来评价曲线
def calcKappa(x_array,y_array):
    s_array = []
    k_array = []
    if(len(x_array) != len(y_array)):
        return(s_array , k_array)

    length = len(x_array)
    temp_s = 0.0
    s_array.append(temp_s)
    for i in range(1 , length):
        temp_s += np.sqrt(np.square(y_array[i] - y_array[i - 1]) + np.square(x_array[i] - x_array[i - 1]))
        s_array.append(temp_s)

    xds,yds,xdds,ydds = [],[],[],[]
    for i in range(length):
        if i == 0:
            xds.append((x_array[i + 1] - x_array[i]) / (s_array[i + 1] - s_array[i]))
            yds.append((y_array[i + 1] - y_array[i]) / (s_array[i + 1] - s_array[i]))
        elif i == length - 1:
            xds.append((x_array[i] - x_array[i-1]) / (s_array[i] - s_array[i-1]))
            yds.append((y_array[i] - y_array[i-1]) / (s_array[i] - s_array[i-1]))
        else:
            xds.append((x_array[i+1] - x_array[i-1]) / (s_array[i+1] - s_array[i-1]))
            yds.append((y_array[i+1] - y_array[i-1]) / (s_array[i+1] - s_array[i-1]))
    for i in range(length):
        if i == 0:
            xdds.append((xds[i + 1] - xds[i]) / (s_array[i + 1] - s_array[i]))
            ydds.append((yds[i + 1] - yds[i]) / (s_array[i + 1] - s_array[i]))
        elif i == length - 1:
            xdds.append((xds[i] - xds[i-1]) / (s_array[i] - s_array[i-1]))
            ydds.append((yds[i] - yds[i-1]) / (s_array[i] - s_array[i-1]))
        else:
            xdds.append((xds[i+1] - xds[i-1]) / (s_array[i+1] - s_array[i-1]))
            ydds.append((yds[i+1] - yds[i-1]) / (s_array[i+1] - s_array[i-1]))
    for i in range(length):
        k_array.append((xds[i] * ydds[i] - yds[i] * xdds[i]) / (np.sqrt(xds[i] * xds[i] + yds[i] * yds[i]) * (xds[i] * xds[i] + yds[i] * yds[i]) + 1e-6));
    return(s_array,k_array)

def referenceline():

    #add some data for test
    x_array = [0.5,1.0,2.0,3.0,4.0,
               5.0,6.0,7.0,8.0,9.0,
              10.0,11.0,12.0,13.0,14.0,
              15.0,16.0,17.0,18.0,19.0]
    y_array = [0.1,0.3,0.2,0.4,0.3,
               -0.2,-0.1,0,0.5,0,
              0.1,0.3,0.2,0.4,0.3,
               -0.2,-0.1,0,0.5,0]
    length = len(x_array)

    #weight , from config
    weight_fem_pos_deviation_ = 1e10 #cost1 - x
    weight_path_length = 1          #cost2 - y
    weight_ref_deviation = 1        #cost3 - z


    P = np.zeros((length,length))
    #set P matrix,from calculateKernel
    #add cost1
    P[0,0] = 1 * weight_fem_pos_deviation_
    P[0,1] = -2 * weight_fem_pos_deviation_
    P[1,1] = 5 * weight_fem_pos_deviation_
    P[length - 1 , length - 1] = 1 * weight_fem_pos_deviation_
    P[length - 2 , length - 1] = -2 * weight_fem_pos_deviation_
    P[length - 2 , length - 2] = 5 * weight_fem_pos_deviation_

    for i in range(2 , length - 2):
        P[i , i] = 6 * weight_fem_pos_deviation_
    for i in range(2 , length - 1):
        P[i - 1, i] = -4 * weight_fem_pos_deviation_
    for i in range(2 , length):
        P[i - 2, i] = 1 * weight_fem_pos_deviation_

    with np.printoptions(precision=0):
        print(P)

    P = P / weight_fem_pos_deviation_
    P = sparse.csc_matrix(P)

    #set q matrix , from calculateOffset
    q = np.zeros(length)

    #set Bound(upper/lower bound) matrix , add constraints for x
    #from CalculateAffineConstraint

    #In apollo , Bound is from road boundary,
    #Config limit with (0.1,0.5) , Here I set a constant 0.2
    bound = 0.2
    A = np.zeros((length,length))
    for i in range(length):
        A[i, i] = 1
    A = sparse.csc_matrix(A)
    lx = np.array(x_array) - bound
    ux = np.array(x_array) + bound
    ly = np.array(y_array) - bound
    uy = np.array(y_array) + bound

    #solve
    prob = osqp.OSQP()
    prob.setup(P,q,A,lx,ux)
    res = prob.solve()
    opt_x = res.x

    prob.update(l=ly, u=uy)
    res = prob.solve()
    opt_y = res.x

    #plot x - y , opt_x - opt_y , lb - ub

    fig1 = plt.figure(dpi = 100 , figsize=(12, 8))
    ax1_1 = fig1.add_subplot(2,1,1)

    ax1_1.plot(x_array,y_array , ".--", color = "grey", label="orig x-y")
    ax1_1.plot(opt_x, opt_y,".-",label = "opt x-y")
    # ax1_1.plot(x_array,ly,".--r",label = "bound")
    # ax1_1.plot(x_array,uy,".--r")
    ax1_1.legend()
    ax1_1.grid(axis="y",ls='--')

    #plot kappa
    ax1_2 = fig1.add_subplot(2,1,2)
    s_orig,k_orig = calcKappa(x_array,y_array)
    s_opt ,k_opt = calcKappa(opt_x,opt_y)
    ax1_2.plot(s_orig , k_orig , ".--", color = "grey", label="orig s-kappa")
    ax1_2.plot(s_opt,k_opt,".-",label="opt s-kappa")
    ax1_2.legend()
    ax1_2.grid(axis="y",ls='--')
    plt.show()


if __name__ == '__main__':
    referenceline()

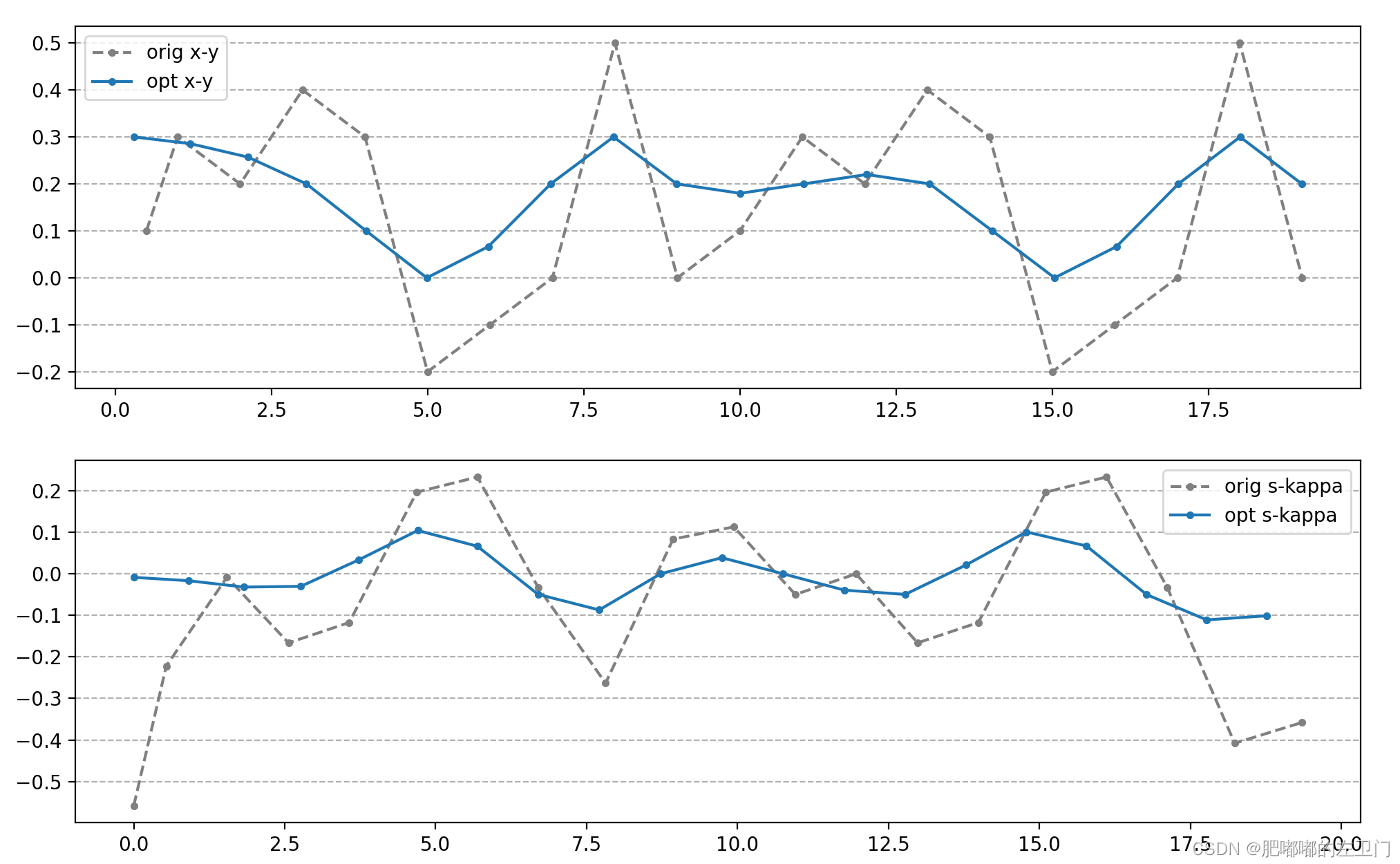
平滑前后的坐标和曲率对比：

肥嘟嘟的左卫门

关注

6
点赞
踩
20

收藏

觉得还不错? 一键收藏
0
评论
决策规划算法二：生成参考线（FEM_POS_DEVIATION_SMOOTHING）

Apollo的的规划算法基于Frenet坐标系，因此道路中心线的平滑性控制着车辆是否左右频繁晃动，而高精地图的道路中心线往往不够平滑。离散点平滑法，包括1，FEM_POS_DEVIATION_SMOOTHING有限元位置差异2，COS_THETA_SMOOTHING余弦）3，QpSplineReferenceLineSmoother（三次样条插值法）4，SpiralReferenceLineSmoother（螺旋曲线法）本文只讲解FEM_POS_DEVIATION_SMOOTHIN.
复制链接

扫一扫