作者主页(文火冰糖的硅基工坊):https://blog.csdn.net/HiWangWenBing
本文网址:https://blog.csdn.net/HiWangWenBing/article/details/119325116
目录
第1章 导数的概述
1.1 导数的定义
导数(Derivative),也叫导函数值,又名微商,是微积分中的重要基础概念。当函数y=f(x)的自变量x在一点x0上产生一个增量Δx时,函数输出值的增量Δy与自变量增量Δx的比值在Δx趋于0时的极限a如果存在,a即为在x0处的导数,记作f'(x0)或df(x0)/dx。

对于可导的函数f(x),x↦f'(x)也是一个函数,称作f(x)的导函数(简称导数)。
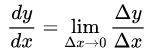

1.2 导数的几何意义
导数是函数的局部性质。一个函数在某一点的导数描述了这个函数在这一点附近的变化率。如果函数的自变量和取值都是实数的话,函数在某一点的导数就是该函数所代表的曲线在这一点上的切线斜率。导数的本质是通过极限的概念对函数进行局部的线性逼近。例如在运动学中,物体的位移对于时间的导数就是物体的瞬时速度。
是所有的函数都有导函数,一个函数也不一定在所有的点上都有导数。
若某函数在某一点导数存在,则称其在这一点可导,否则称为不可导。然而,可导的函数一定连续;不连续的函数一定不可导。
导数与物理、几何、代数关系密切:
- 在几何中可求切线;
- 在代数中可求瞬时变化率;
- 在物理中可求速度、加速度。
1.3 导数在深度学习中的应用
(1)误差或损失函数loss的优化
用于求loss函数的极小值,即用于求神经元参数(Wi,Bi)在什么情况下,可以使得损失loss函数的输出值最小。
第2章 函数的极值与导数的关系
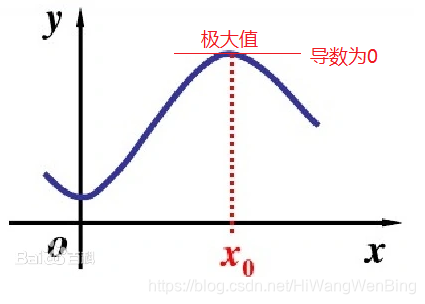
2.1 函数的极值
(1)极大值
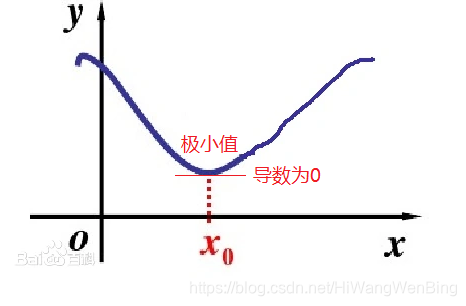
(2)极小值
2.2 导数与函数的单调性
一般地,设函数y=f(x)在某个区间内有导数,
如果在这个区间y'>0,那么函数y=f(x)在这个区间上为单调增函数:
如果在这个区间y'<0,那么函数y=f(x)在这个区间上为减函数;
如果在这个区间y'=0,那么函数y=f(x)在这个区间上为常数函数
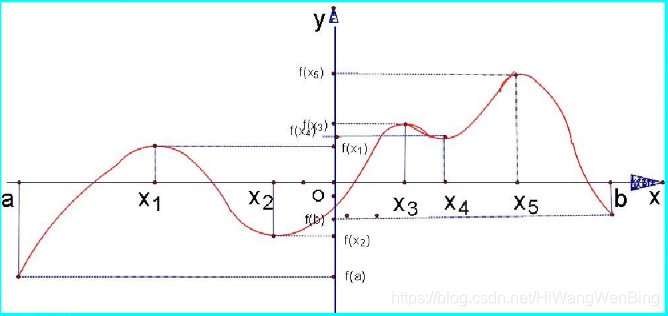
2.3 最大值与极大值区别
-
最大值是函数中最大的值,而极大值不是。
-
最大值一定高于函数中其他的值,极大值可以小于极小值。
-
最大值的值只有一个,而极大值的值可以有无限个。
-
最大值的定义区间为函数定义域,极大值可以自定义区间。
第4章 用导数求函数的极值
4.1 导函数法
(1)求出导函数 -- 数学公式法
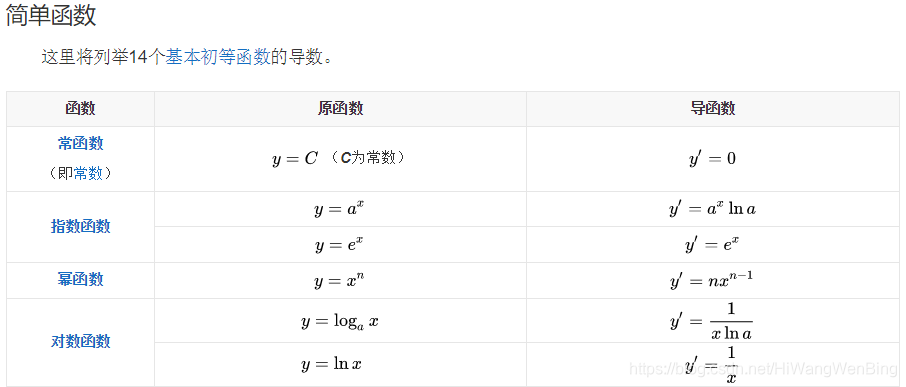
(2)令导函数 = 0
(3)解方程,找出导数等于0的点。
(4)把x带入到原方程,得到导数为0点时候的y值,就是极值。
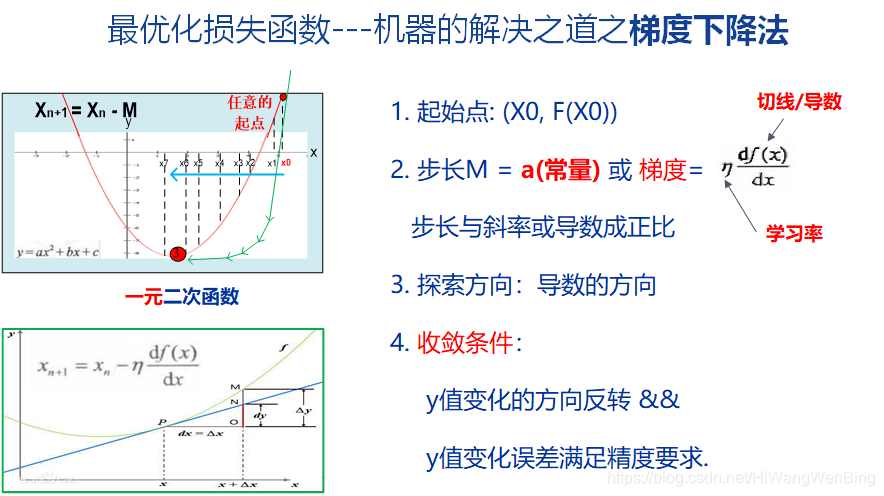
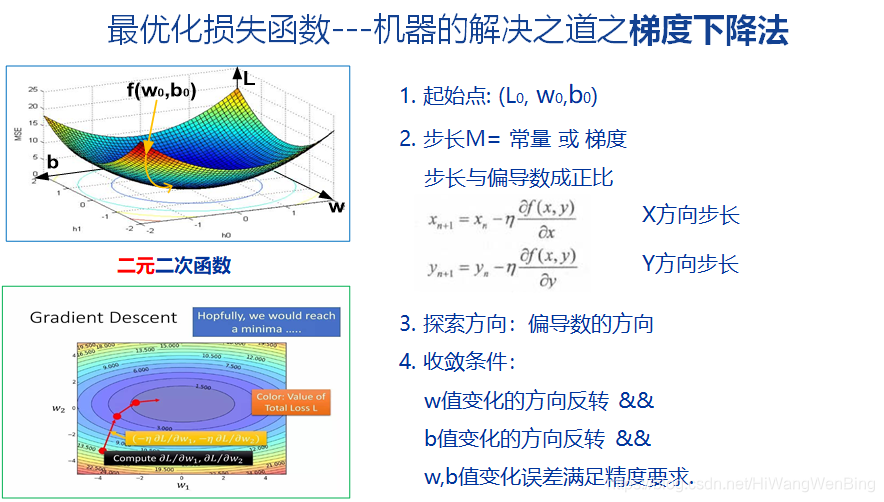
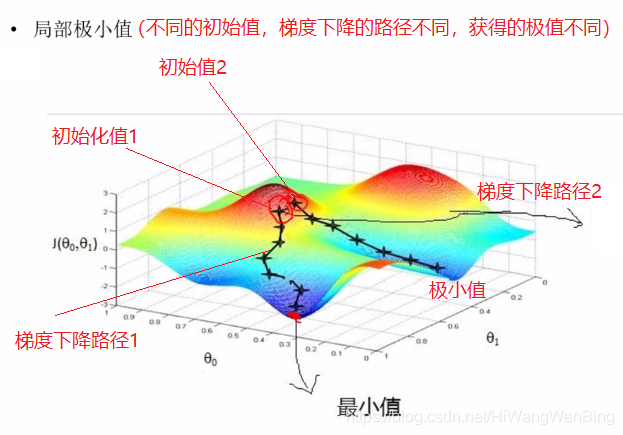
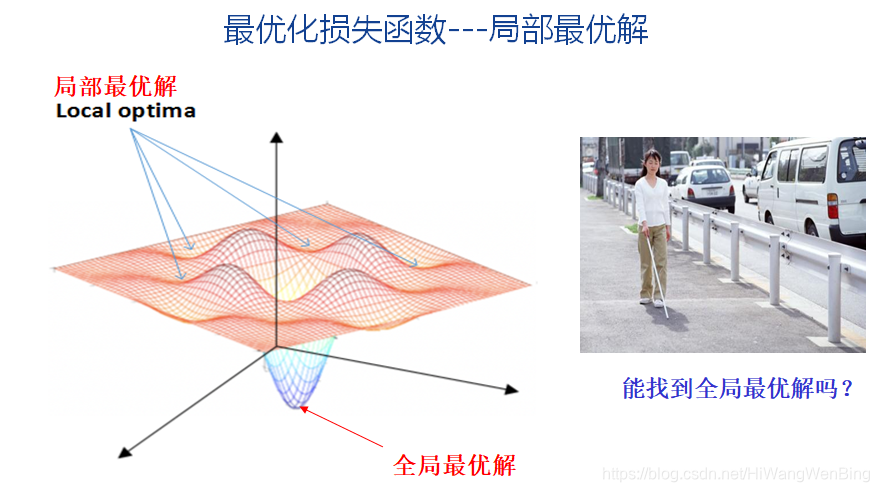
4.2 逐渐逼近法 -- 梯度下降法

作者主页(文火冰糖的硅基工坊):https://blog.csdn.net/HiWangWenBing
本文网址:https://blog.csdn.net/HiWangWenBing/article/details/119325116











 本文介绍了导数的基本概念及其几何意义,探讨了导数与函数极值的关系,并讲解了如何利用导数来求解函数的极值问题,特别是在深度学习中的应用。
本文介绍了导数的基本概念及其几何意义,探讨了导数与函数极值的关系,并讲解了如何利用导数来求解函数的极值问题,特别是在深度学习中的应用。


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










