2023年IMO几何预选题第4题

在锐角 $△ABC$ 中, $AB<AC$, $\Omega$ 是外接圆, $S$ 是弧 $BAC$ 的中点. 过 $A$ 作 $BC$ 的垂线交 $BS$ 于点 $D$, 交 $\Omega$ 于点 $E$. 过 $D$ 作 $BC$ 的平行线交直线 $BE$ 于点 $L$, 设 $△BDL$ 的 外接圆 $\omega$ 与 $\Omega$ 交于另一点 $F$. 求证: $\omega$ 在 $P$ 处的切线与直线 $BS$ 的交点在 $\angle BAC$ 的平分线上.

证明:

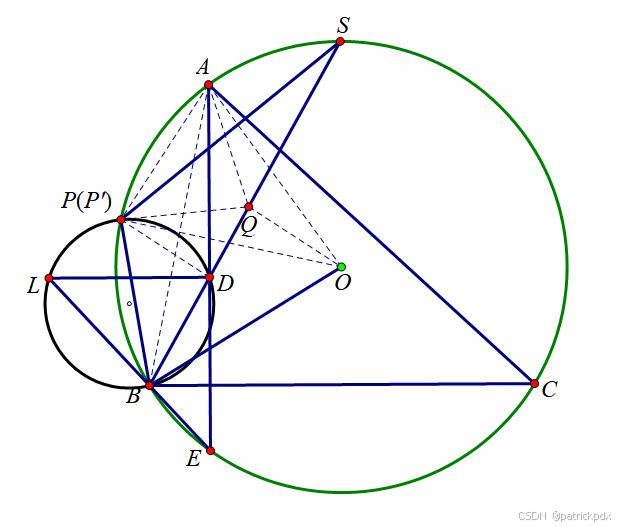
$\angle DPB=\angle DLB=\angle EBC=\angle EAC=\frac{\pi }{2}-C$

$\therefore AP\perp PD$. 设 ($\angle BAC$ 的平分线交 $BS$ 于点 $Q$).

设以 $Q$ 为圆心, $AQ$ 为半径的圆交 $(ABC)$ 于 $P^{\prime }$.

倒角可知, $\angle ADQ=\angle OAQ=\angle ABS=|\frac{B}{2}-\frac{C}{2}|$

$\therefore △AQD\sim △BQA$, $A{Q}^2=(A{P}^{\prime }{)}^2=QD\cdot QB$

进而 $△DQ{P}^{\prime }\sim △PQB$, $\angle D{P}^{\prime }Q=\angle PBS$

设弧 $B{P}^{\prime }$所对的圆周角为 $x$.

$\angle D{P}^{\prime }Q=\frac{\pi }{2}-\frac{A}{2}-x$

显然, $OQ\perp A{P}^{\prime }$, 且 $\angle Q{P}^{\prime }O=\angle QAO=|\frac{B}{2}-\frac{C}{2}|$

不妨设 $\angle B>\angle C$

则易知 $\angle D{P}^{\prime }O=\angle D{P}^{\prime }Q-\angle Q{P}^{\prime }O=C-x=\angle POQ$.

$\therefore OP$ 平行于 $D{P}^{\prime }$. $D{P}^{\prime }\perp A{P}^{\prime }$. 进而 $P$ 和 $P^{\prime }$ 同为以 $AD$ 为直径的圆与 $(ABC)$ 的交点, 因此重合.

$\because Q{P}^2=QD\cdot QB$.

$\therefore QP$ 与 $(DLB)$ 相切.