种子填充法原理
关于种子填充法的详细原理可以参考OpenCV_连通区域分析(Connected Component Analysis/Labeling)
大致算法如下:
设二值化图像A中,像素值为255的点是前景,为0的点是背景。A(x, y)为坐标(x, y)处的像素值,遍历图像的每个像素:
1、 如果像素值不等于255,则继续访问下一个元素。
2、 如果像素值为A(x, y) = 255,则新建一个新的label,当前值A(x, y) = label,并且
-
a. 检查其4个邻域,如果有属于前景的像素也给它赋予label值,并将它的坐标压栈。
-
b. 弹出栈顶坐标,重复a的过程,知道堆栈为空。
此时,便找到了一个连通区域,该区域内的像素值被标记为label。
3、 重复1、2的过程,检测出所有的区域。

废话少说,上代码!
实现程序
该程序基于OpenCV2.4.9 和VS2010平台:
#include <opencv2\opencv.hpp>
#include <iostream>
#include <vector>
#include <stack>
using namespace std;
using namespace cv;
typedef struct _Feather
{
int label;
int area;
Rect boundingbox;
} Feather;
int bwLabel(Mat & src, Mat & dst, vector<Feather> & featherList)
{
int rows = src.rows;
int cols = src.cols;
int labelValue = 0;
Point seed, neighbor;
stack<Point> pointStack;
int area = 0;
int leftBoundary = 0;
int rightBoundary = 0;
int topBoundary = 0;
int bottomBoundary = 0;
Rect box;
Feather feather;
featherList.clear();
dst.release();
dst = src.clone();
for( int i = 0; i < rows; i++)
{
uchar *pRow = dst.ptr<uchar>(i);
for( int j = 0; j < cols; j++)
{
if(pRow[j] == 255)
{
area = 0;
labelValue++;
seed = Point(j, i);
dst.at<uchar>(seed) = labelValue;
pointStack.push(seed);
area++;
leftBoundary = seed.x;
rightBoundary = seed.x;
topBoundary = seed.y;
bottomBoundary = seed.y;
while(!pointStack.empty())
{
neighbor = Point(seed.x+1, seed.y);
if((seed.x != (cols-1)) && (dst.at<uchar>(neighbor) == 255))
{
dst.at<uchar>(neighbor) = labelValue;
pointStack.push(neighbor);
area++;
if(rightBoundary < neighbor.x)
rightBoundary = neighbor.x;
}
neighbor = Point(seed.x, seed.y+1);
if((seed.y != (rows-1)) && (dst.at<uchar>(neighbor) == 255))
{
dst.at<uchar>(neighbor) = labelValue;
pointStack.push(neighbor);
area++;
if(bottomBoundary < neighbor.y)
bottomBoundary = neighbor.y;
}
neighbor = Point(seed.x-1, seed.y);
if((seed.x != 0) && (dst.at<uchar>(neighbor) == 255))
{
dst.at<uchar>(neighbor) = labelValue;
pointStack.push(neighbor);
area++;
if(leftBoundary > neighbor.x)
leftBoundary = neighbor.x;
}
neighbor = Point(seed.x, seed.y-1);
if((seed.y != 0) && (dst.at<uchar>(neighbor) == 255))
{
dst.at<uchar>(neighbor) = labelValue;
pointStack.push(neighbor);
area++;
if(topBoundary > neighbor.y)
topBoundary = neighbor.y;
}
seed = pointStack.top();
pointStack.pop();
}
box = Rect(leftBoundary, topBoundary, rightBoundary-leftBoundary, bottomBoundary-topBoundary);
rectangle(src, box, 255);
feather.area = area;
feather.boundingbox = box;
feather.label = labelValue;
featherList.push_back(feather);
}
}
}
return labelValue;
}
int main(int argc, char *argv[])
{
Mat src(imread("shape.jpg", 0));
if(src.empty())
exit(-1);
threshold(src, src, 127, 255, THRESH_BINARY);
vector<Feather> featherList;
Mat dst;
cout << "连通域数量: " << bwLabel(src, dst, featherList) << endl;
for( int i = 0; i < dst.rows; i++)
{
uchar *p = dst.ptr<uchar>(i);
for( int j = 0; j < dst.cols; j++)
{
p[j] = 30*p[j];
}
}
cout << "标号" << "\t" << "面积" << endl;
for(vector<Feather>::iterator it = featherList.begin(); it < featherList.end(); it++)
{
cout << it->label << "\t" << it->area << endl;
rectangle(dst, it->boundingbox, 255);
}
imshow("src", src);
imshow("dst", dst);
waitKey();
destroyAllWindows();
system("pause");
return 0;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
- 156
- 157
- 158
- 159
- 160
- 161
- 162
- 163
运行结果:
原图:

检测结果:
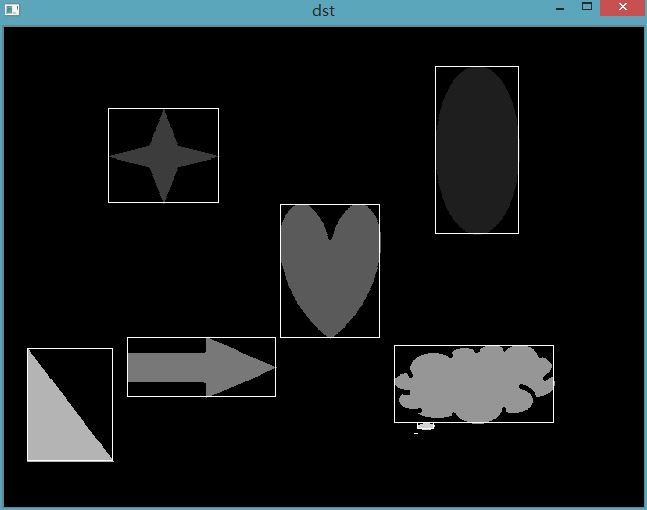
特征清单:
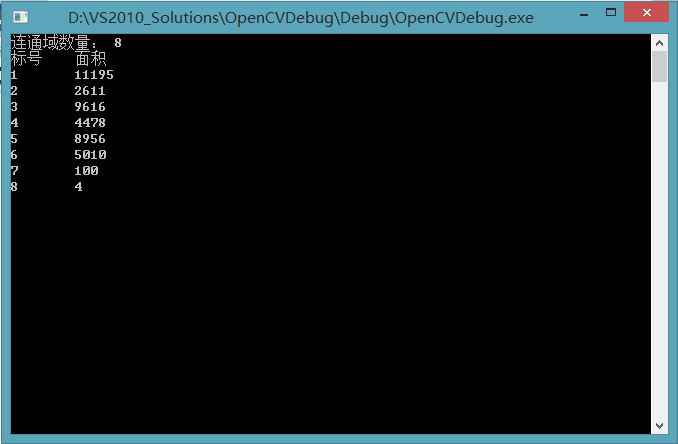





























 6802
6802

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








