概率论：随机变量之非离散变量

在讲非离散变量之前，先要讲讲分布函数：

相信你也发现了，这就是概率密度函数的积分。

分布函数有几条性质：

 有了分布函数这个工具以后，我们就可以学习连续的随机变量了。

概率密度就是分布函数的微分。

概率密度的性质没什么好说的，但有一条挺有意思：

可以理解为“区间”无限小，可能性就没有了。

接下来讲讲几种分布类型：

就是密度处处相等的意思。

指数分布有一个很有意思的特性：

正态分布：

 

还有标准正态分布：

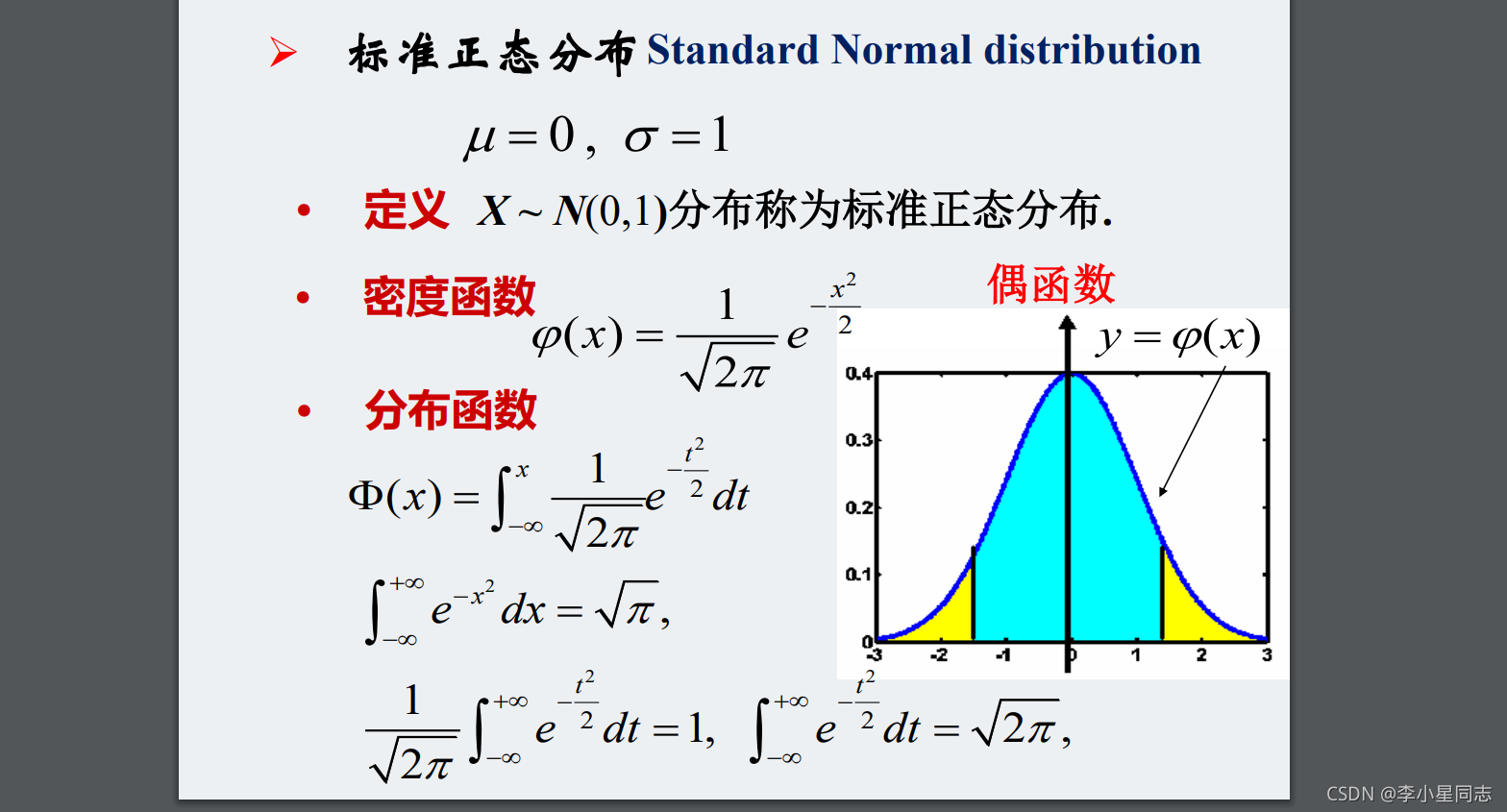
注意，密度是小fai,分布是大fai。

普通的正态分布也可以变成标准的：

 因此，普通的正态分布也可以用查表的方式求出来了：

接下来就有了经典的3欧比噶法则：

这个3欧比噶相当于标准正态分布的3.

接下来就要学X的函数的性质了：

那很多变量是非离散的呀，怎么办？：

也就是说，求的时候从分布函数入手，因为分布函数可以直接转换，和刚刚的正态分布有点像。

 我们特别地拿正态分布举个例子：

刚刚的普通正态分布变成标准正态分布其实就是一个特殊例子。

于是我们有了一些结论：

真的吗？我觉得直接写更快呀。数学问题嘛。

这个也很好证。