假设检验通过统计学手段判断样本数据是否支持某个假设,从而基于数据作出推断。
1. T检验(T-test)
T检验适用于比较2个样本平均值之间是否存在显著差异。
1.1 T检验原理
假设2个样本有相同的分布,如果2个样本平均值差异显著,则表明两者可能为不同分布。
原假设(H0):2个样本平均值无显著差异,即 μ1=μ2。
备择假设(H1):2个样本平均值有显著差异,即 μ1≠μ2 。
1.2 T检验公式
对于独立样本t检验(又称为双样本t检验):
分子表示2个样本的平均值之差,分母表示2个样本各自方差平方比上样本数量的算术平方根。
从下图公式可以看出,T检验需要计算t值,通过其判断2个样本平均值是否存在显著差异。

结论:
t值通过查找t分布表可得到p值,p值越小,越说明样本间差异显著;如果p值小于显著性水平阈值(通常为0.05),则拒绝原假设H0。
1.3 T检验适用范围:
T检验计算简单,适用于正态分布的样本数据,并要求比较样本之间方差大小相差较小;但当样本分布为非正态分布且样本数量较少,T检验一般不太适用。
在实际应用中,可用于比较实验组和控制组的2个样本的均值差异是否显著。
1.4 python实现实验组数据和对照组数据的T检验
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from scipy import stats
# 生成2个不同均值的样本数据(实验 VS 对照)
np.random.seed(123)
# 平均值为10,标准差为3,数据数量100个
experiment_data = np.random.normal(10, 3, 100)
# 平均值为15,标准差为4,数据数量100个
control_data = np.random.normal(15, 4, 100)
# t-test 两组数据的均值
t_stat, p_value = stats.ttest_ind(experiment_data, control_data)
print(f"T-value: {t_stat}, P-value: {p_value}")
# T-value: -9.353755620233024, P-value: 1.8665012625102836e-17
####### 核密度图 ########
# 设置图大小
plt.figure(figsize=(10, 6))
sns.kdeplot(experiment_data, label="experiment data (Mean=10)", shade=True)
sns.kdeplot(control_data, label="control data (Mean=15)", shade=True)
plt.legend()
plt.show()
####### 箱线图 #######
sns.boxplot(data=[experiment_data, control_data])
plt.xticks([0, 1], ["experiment data", "control data"])
plt.suptitle("T-Test between experiment and control", fontsize=12)
plt.tight_layout()
plt.show()
结论:
t值(T-value: -9.353755620233024),p值(P-value: 1.8665012625102836e-17)小于0.05,拒绝原假设H0,即2个样本数据集存在显著差异。
核密度图
核密度图曲线峰值为2个数据集的平均值,反应了2个数据集的数据分布情况。

箱线图
箱线图上横线和下横线分别表示上四分位数、下四分位数,箱子中间横线表示平均值,原点表示异常值,可直观看出2个数据集在均值上的差异。

2. Z检验(Z-test)
Z检验主要用于样本数量较多且已知总体的标准差的情况,可检验单个样本与总体样本平均值之间的差异,也可以比较2个样本之间平均值的差异。
2.1 Z检验原理
原假设(H0):样本均值与总体均值无显著差异,或两个样本均值无显著差异。
备择假设(H1):样本均值与总体均值有显著差异,或两个样本均值有显著差异。
2.2 Z检验公式
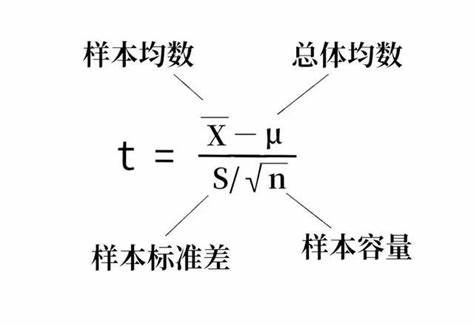
|Z|值与P值结论

2.3 Z检验适用范围:
样本较大、已知标准差,并不适用于小样本数据。
2.4 python实现单个样本和总体样本的Z检验
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from scipy import stats
# 已知总体均值和方差数据
# 假设总体均值为15,总体SD为3.5,样本数量100个,进行单样本z检验
total_mean = 15
total_sd = 3.5
n = 100
np.random.seed(123)
# 从正态分布总体数据中获取样本数据
sample = np.random.normal(total_mean , total_sd , n)
# 求样本均值和标准差
sample_mean = np.mean(sample)
sample_std = np.std(sample, ddof=1)
# 计算公式
p_value = 2 * (1 - stats.norm.cdf(abs((sample_mean - total_mean) / (total_sd / np.sqrt(n)))))
print(f"Z-value: {z_stat}, P-value: {p_value}")
# z_value: -3.9513638778274593, P-value: 7.770706713938758e-05
plt.figure(figsize=(10, 6))
# 核密度图
sns.kdeplot(sample, label="Sample Distribution", shade=True)
# 添加总体均值和假设均值的竖线
plt.axvline(np.mean(sample), linestyle='--', label='Sample Mean')
plt.axvline(total_mean, color='red', linestyle='--', label='Total sample Mean')
plt.legend()
plt.title("Z-Test")
plt.tight_layout()
plt.show()
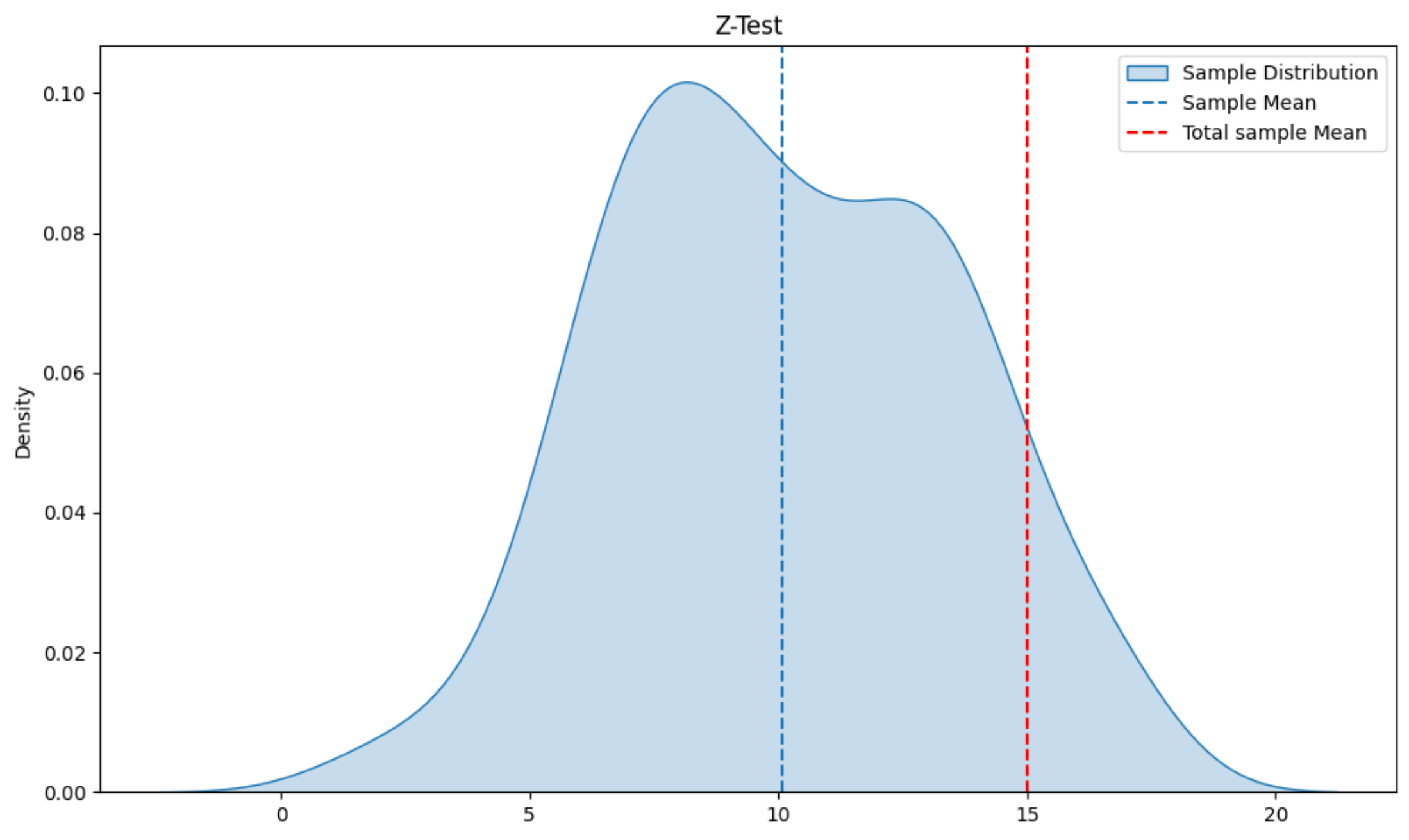 结论:
结论:
通过z统计量和p值,我们可以判断样本均值与假设均值是否有显著差异。如果p值小于0.05,则拒绝原假设;上述z-value绝对值2.68且大于p-value小于0.01, 单样本与总体均值差异非常显著。


























 177
177

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










