【MIMO-OFDM】基于Matlab模拟天线阵列几何形状大规模 MIMO-OFDM系统半盲结构化信道估计性能的影响分析

✅作者简介：热爱科研的Matlab仿真开发者，修心和技术同步精进，代码获取、论文复现及科研仿真合作可私信。

🍎个人主页：Matlab科研工作室

🍊个人信条：格物致知。

更多Matlab完整代码及仿真定制内容点击👇

智能优化算法       神经网络预测       雷达通信       无线传感器        电力系统

信号处理              图像处理               路径规划       元胞自动机        无人机

物理应用        机器学习

🔥 内容介绍

随着5G及未来无线通信技术的快速发展，大规模MIMO技术因其高数据速率和高频谱效率等优势而备受关注。然而，大规模MIMO系统面临着信道估计复杂度高、训练开销大的挑战。半盲信道估计技术利用信道先验信息，降低了训练开销，并提高了信道估计性能，是解决这一问题的有效方法。本文将对天线阵列几何形状对大规模MIMO-OFDM系统半盲结构化信道估计性能的影响进行深入分析。

1. 引言

大规模MIMO技术，即Massive MIMO，通过在基站配备数百甚至上千根天线，可大幅提高系统容量和能量效率，成为未来无线通信的关键技术。然而，大规模MIMO系统中信道估计的复杂度和训练开销也随之大幅增加。为了克服这一挑战，近年来，半盲信道估计技术得到了广泛关注。半盲信道估计技术利用信道先验信息，例如信道稀疏性、空间相关性等，以较少的训练开销实现准确的信道估计。

在半盲信道估计中，信道结构的先验信息对于估计性能至关重要。而天线阵列的几何形状直接影响着信道结构。不同的天线阵列几何形状会导致不同的信道空间相关性，进而影响半盲信道估计的性能。因此，深入分析天线阵列几何形状对半盲结构化信道估计性能的影响，对于优化大规模MIMO系统的设计和性能至关重要。

2. 系统模型

考虑一个单小区大规模MIMO-OFDM系统，基站配备𝑁N根天线，用户配备𝑀M根天线。假设系统采用OFDM调制，每个子载波上的信道可以表示为一个𝑀×𝑁M×N的矩阵，其元素表示不同天线之间的信道增益。

在半盲结构化信道估计中，假设信道矩阵可以分解为一个低秩矩阵和一个稀疏矩阵之和：

𝐻

​=AB+S

3. 天线阵列几何形状的影响

天线阵列的几何形状会影响信道矩阵的结构，进而影响半盲信道估计的性能。常见的几种天线阵列几何形状包括：

• 均匀线性阵列 (ULA)：天线均匀分布在一条直线上，这种阵列具有较高的空间分辨率，但其在垂直于阵列方向上的空间相关性较差。

• 均匀圆形阵列 (UCA)：天线均匀分布在圆周上，这种阵列具有全方向的空间覆盖能力，但其在不同方向上的空间分辨率不同。

• 非均匀线性阵列 (NULA)：天线非均匀分布在直线上，这种阵列可以灵活调整天线间距，以优化信道估计性能，但其设计复杂度较高。

不同的天线阵列几何形状会影响信道的空间相关性，进而影响AA矩阵的秩和SS矩阵的稀疏度，最终影响半盲信道估计的性能。例如，ULA阵列在水平方向上的空间相关性较高，而在垂直方向上的空间相关性较低，这会使得AA矩阵的秩较低，而SS矩阵的稀疏度较高。

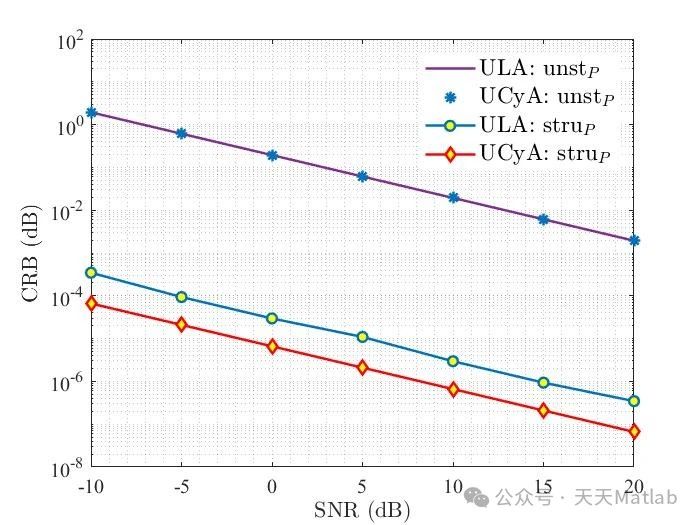
4. 仿真结果与分析

为了验证不同天线阵列几何形状对半盲结构化信道估计性能的影响，我们进行了仿真实验。在仿真中，我们使用不同的天线阵列几何形状，包括ULA、UCA和NULA，并使用不同的半盲结构化信道估计算法，例如基于低秩矩阵分解的算法和基于稀疏矩阵恢复的算法。

仿真结果表明：

• ULA阵列: 在水平方向上，ULA阵列可以有效地利用空间相关性，从而实现较高的信道估计精度；但在垂直方向上，其性能会受到限制。

• UCA阵列: UCA阵列在不同方向上的空间分辨率不同，这导致其信道估计精度在不同方向上存在差异。

• NULA阵列: NULA阵列可以通过优化天线间距来提高信道估计精度，但其设计复杂度较高。

仿真结果还表明，对于不同的信道估计算法，不同天线阵列几何形状的性能差异也存在不同。例如，基于低秩矩阵分解的算法更适合于ULA阵列，而基于稀疏矩阵恢复的算法更适合于NULA阵列。

5. 结论

天线阵列的几何形状对大规模MIMO-OFDM系统半盲结构化信道估计性能有显著影响。ULA阵列在水平方向上具有较高的性能，而UCA阵列具有全方向的空间覆盖能力，NULA阵列可以通过优化天线间距来提高性能。选择合适的阵列形状和信道估计算法，可以有效地提高半盲结构化信道估计性能。

⛳️ 运行结果

📣 部分代码

clear all;close all;clc; ​addpath('./funcs');​%% Declear​Nt      = 2;                    % number of transmit antennas​N_r_UCA = 8:8:64;               % UCANr_ULA  = 4;                    % UCyAsnr_i   = 5;loop    = 100;​gamma_f = {};AOA_f = {};ZOA_f = {};​CRB_SB_ULA_f         = [];CRB_SB_ULA_spec_f    = [];CRB_SB_UCyA_f        = [];CRB_SB_UCyA_spec_f   = [];​for Nr_UCA = N_r_UCA    fprintf('Working at Nr_UCA: %d.\n', Nr_UCA);    tic​    Nr      = Nr_UCA * Nr_ULA;      % ULA        L       = 1;                    % Channel order    d_H     = 4;                    % Number of propagation paths        Pxp     = 1;    K       = 64;                   % OFDM subcarriers    F       = dftmtx(K);    FL      = F(:,1:L);    sigmax2 = 1; ​    %% Generate position of elements in arrays    d_ULA_nor   = 0.5;    d_UCA_nor   = 0.5;    R_nor       = 0.5 * d_UCA_nor/sin(pi/Nr_UCA);        ULA_elements_nor    = zeros(3, 1, Nr);    UCyA_elements_nor   = zeros(3, Nr_ULA, Nr_UCA);        for Nr_index=1:Nr        ULA_elements_nor(1, 1, Nr_index) = (Nr_index-1) * d_UCA_nor;        ULA_elements_nor(2, 1, Nr_index) = 0;        ULA_elements_nor(3, 1, Nr_index) = 0;    end        for Nr_ULA_index=1:Nr_ULA        for Nr_UCA_index=1:Nr_UCA            UCyA_elements_nor(1, Nr_ULA_index, Nr_UCA_index) = R_nor * sin((Nr_UCA_index-1)*(2*pi/Nr_UCA)) ;         % x            UCyA_elements_nor(2, Nr_ULA_index, Nr_UCA_index) = R_nor * cos((Nr_UCA_index-1)*(2*pi/Nr_UCA)) ;         % y            UCyA_elements_nor(3, Nr_ULA_index, Nr_UCA_index) = (Nr_ULA_index-1) * d_ULA_nor;                         % z        end    end        %% Signal Generation    % we use the Zadoff-Chu sequences    U = 1:2:100;    ZC_p = [];    for u = 1 : Nt        for k = 1 : K            ZC(k,u) = sqrt(Pxp) * exp( ( -1i * pi * U(u) * (k-1)^2 ) / K );        end        ZC_p = [ZC_p; ZC(:,u)];    end        X = [];    for ii = 1 : Nt        X  = [X diag(ZC(:,ii))*FL];   

🔗 参考文献

[1] 董玥昕.基于子空间的改进STBC-MIMO-OFDM系统半盲信道估计算法[D].吉林大学,2007.DOI:CNKI:CDMD:2.2007.092773.

[2] 任雁,李艳萍.基于EM算法的MIMO-OFDM系统半盲信道估计研究[J].长治学院学报, 2011, 28(2):3.DOI:10.3969/j.issn.1673-2014.2011.02.006.

[3] 王忆冉,朱留存,蒋昊天,等.基于CS的大规模MIMO-OFDM信道估计[J].科技与创新, 2020(4):2.DOI:CNKI:SUN:KJYX.0.2020-04-059.

🎈 部分理论引用网络文献，若有侵权联系博主删除

👇 关注我领取海量matlab电子书和数学建模资料

🎁  私信完整代码和数据获取及论文数模仿真定制🌈

🌈 各类智能优化算法改进及应用

生产调度、经济调度、装配线调度、充电优化、车间调度、发车优化、水库调度、三维装箱、物流选址、货位优化、公交排班优化、充电桩布局优化、车间布局优化、集装箱船配载优化、水泵组合优化、解医疗资源分配优化、设施布局优化、可视域基站和无人机选址优化、背包问题、 风电场布局、时隙分配优化、 最佳分布式发电单元分配、多阶段管道维修、 工厂-中心-需求点三级选址问题、 应急生活物质配送中心选址、 基站选址、 道路灯柱布置、 枢纽节点部署、 输电线路台风监测装置、 集装箱调度、 机组优化、 投资优化组合、云服务器组合优化、 天线线性阵列分布优化、CVRP问题、VRPPD问题、多中心VRP问题、多层网络的VRP问题、多中心多车型的VRP问题、 动态VRP问题、双层车辆路径规划（2E-VRP）、充电车辆路径规划（EVRP）、油电混合车辆路径规划、混合流水车间问题、 订单拆分调度问题、 公交车的调度排班优化问题、航班摆渡车辆调度问题、选址路径规划问题、港口调度

🌈 机器学习和深度学习时序、回归、分类、聚类和降维

2.1 bp时序、回归预测和分类

2.2 ENS声神经网络时序、回归预测和分类

2.3 SVM/CNN-SVM/LSSVM/RVM支持向量机系列时序、回归预测和分类

2.4 CNN/TCN卷积神经网络系列时序、回归预测和分类

2.5 ELM/KELM/RELM/DELM极限学习机系列时序、回归预测和分类

2.6 GRU/Bi-GRU/CNN-GRU/CNN-BiGRU门控神经网络时序、回归预测和分类

2.7 ELMAN递归神经网络时序、回归\预测和分类

2.8 LSTM/BiLSTM/CNN-LSTM/CNN-BiLSTM/长短记忆神经网络系列时序、回归预测和分类

2.9 RBF径向基神经网络时序、回归预测和分类

2.10 DBN深度置信网络时序、回归预测和分类

2.11 FNN模糊神经网络时序、回归预测

2.12 RF随机森林时序、回归预测和分类

2.13 BLS宽度学习时序、回归预测和分类

2.14 PNN脉冲神经网络分类

2.15 模糊小波神经网络预测和分类

2.16 时序、回归预测和分类

2.17 时序、回归预测预测和分类

2.18 XGBOOST集成学习时序、回归预测预测和分类

方向涵盖风电预测、光伏预测、电池寿命预测、辐射源识别、交通流预测、负荷预测、股价预测、PM2.5浓度预测、电池健康状态预测、用电量预测、水体光学参数反演、NLOS信号识别、地铁停车精准预测、变压器故障诊断

🌈图像处理方面

图像识别、图像分割、图像检测、图像隐藏、图像配准、图像拼接、图像融合、图像增强、图像压缩感知

🌈 路径规划方面

旅行商问题（TSP）、车辆路径问题（VRP、MVRP、CVRP、VRPTW等）、无人机三维路径规划、无人机协同、无人机编队、机器人路径规划、栅格地图路径规划、多式联运运输问题、 充电车辆路径规划（EVRP）、 双层车辆路径规划（2E-VRP）、 油电混合车辆路径规划、 船舶航迹规划、 全路径规划规划、 仓储巡逻

🌈 无人机应用方面

无人机路径规划、无人机控制、无人机编队、无人机协同、无人机任务分配、无人机安全通信轨迹在线优化、车辆协同无人机路径规划

🌈 通信方面

传感器部署优化、通信协议优化、路由优化、目标定位优化、Dv-Hop定位优化、Leach协议优化、WSN覆盖优化、组播优化、RSSI定位优化、水声通信

🌈 信号处理方面

信号识别、信号加密、信号去噪、信号增强、雷达信号处理、信号水印嵌入提取、肌电信号、脑电信号、信号配时优化、心电信号、DOA估计、编码译码、变分模态分解、管道泄漏、滤波器、数字信号处理+传输+分析+去噪、数字信号调制、误码率、信号估计、DTMF、信号检测

🌈电力系统方面

微电网优化、无功优化、配电网重构、储能配置、有序充电、MPPT优化

🌈 元胞自动机方面

交通流 人群疏散 病毒扩散 晶体生长 金属腐蚀

🌈 雷达方面

卡尔曼滤波跟踪、航迹关联、航迹融合、SOC估计、阵列优化、NLOS识别