读《微波工程(第三版)》笔记 (3：介质中的边界条件)

The Darndest

已于 2022-10-11 20:05:32 修改

阅读量1.9k

点赞数 3

分类专栏：微波工程文章标签：射频工程

于 2022-10-11 11:42:46 首次发布

本文链接：https://blog.csdn.net/Within_Me/article/details/127258189

版权

微波工程专栏收录该内容

13 篇文章 11 订阅

订阅专栏

求解微分形式的麦克斯韦方程组(详见笔记1) ，必须已知边界上的值时，才能有完整切唯一的解。

常用的方法是：在一定的区域求解无源麦克斯韦方程组获得带有未知系数的通解，再利用边界条件来求得这些系数

我的理解：麦克斯韦方程组+边界条件=特解

一般材料分界面上的场

分析模型

考虑两种媒质之间的平面界面，如图3.1所示：

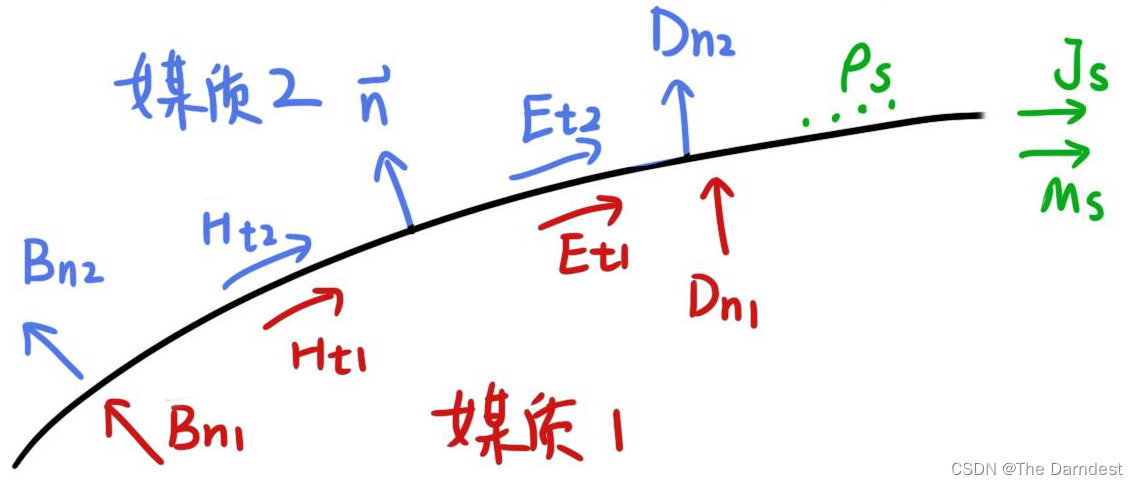
图 3.1

其中，两个介质内的场和分界面上的场都用颜色进行了区分。

利用积分形式的麦克斯韦方程组来推导分界面上的的法向、切向场的边界条件。

我们可以选取如图3.2所示的闭合高斯曲面作为分析工具，主要用来分析电位移矢量和磁感应强度。它是一个圆柱面，上下底面横跨两种媒质，并且要求高度h->0。

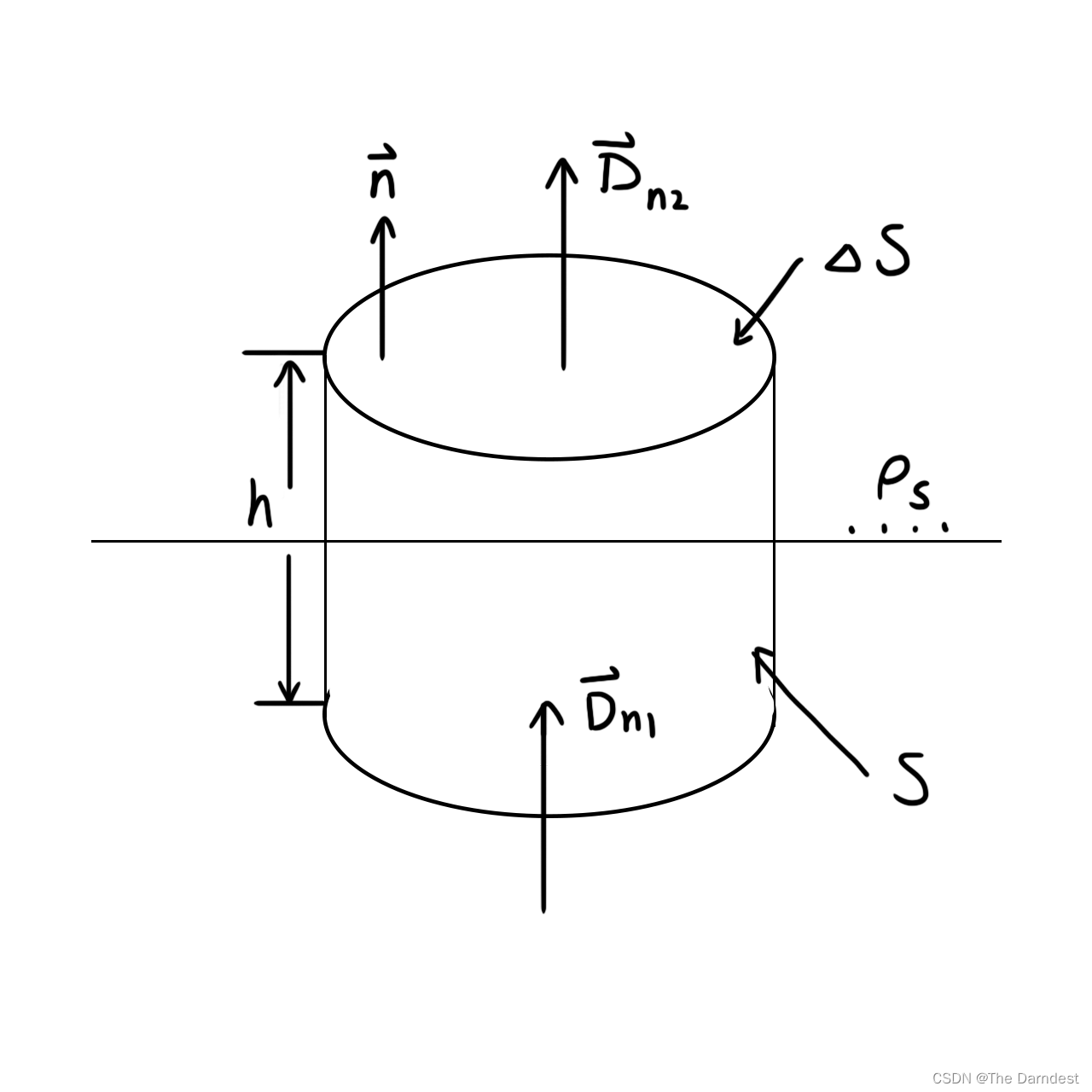
图 3.2

分析磁场、电场时，可以使用图3.3

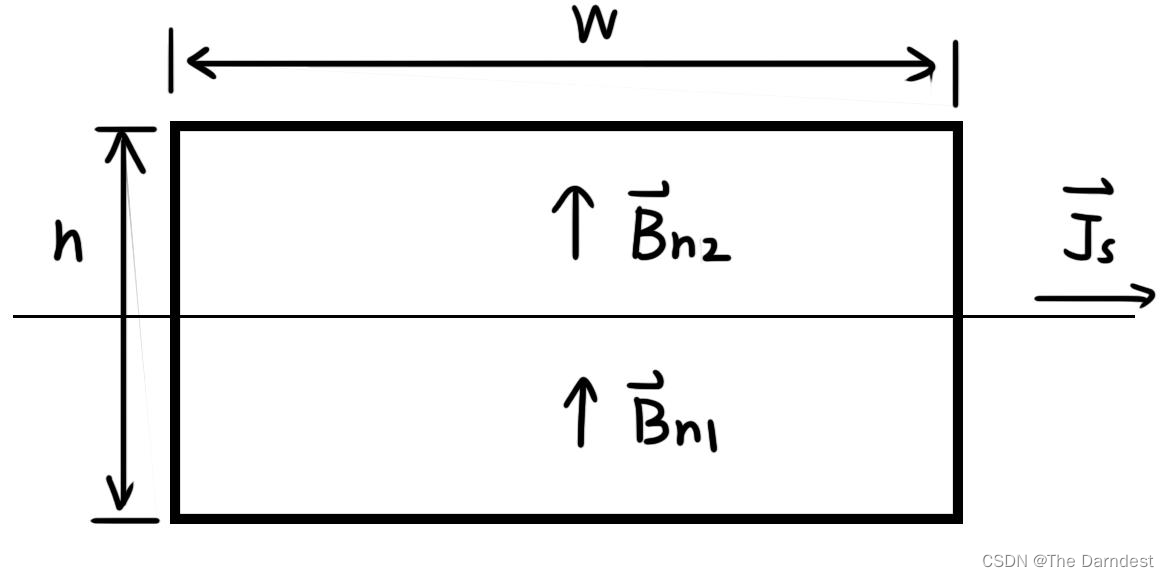
图 3.3（这里有点小错误，别管两个磁感应强度）

电位移矢量

电位移矢量满足高斯定理：

$\oint _{S}\overrightarrow{D}\cdot d\overrightarrow{s}=\int _{V}\rho d\nu=Q$

由于高度h趋于0，此时圆柱侧面的电位移通量贡献为0，可以简化为：

$\begin{} {\color{black} \Delta S\cdot D_{n2} - \Delta S\cdot D_{n1} = \Delta S\cdot \rho_{s}} \\\\ D_{n2}-D_{n1}=\rho_{s} \end{}$

如果写成矢量形式，则为：

$\widehat{n}\cdot (\overrightarrow{D_{2}}-\overrightarrow{D_{1}})=\rho_{s}$

也就是：电位移矢量在边界上法向不连续，数值相差为分界面上的面电荷密度。

磁感应强度

同样地，将磁通连续性方程的积分形式写出：

$\oint _{S}\overrightarrow{B}\cdot d\overrightarrow{s}=0$

同样由于侧面的磁通量贡献为0，可写出：

$\begin{} {\color{black} \Delta S\cdot B_{n2} - \Delta S\cdot B_{n1} = 0} \\\\ B_{n2}-B_{n1}=0 \end{}$

矢量形式则是：

$\begin{} {\color{black} \widehat{n}\cdot (\overrightarrow{B_{2}}-\overrightarrow{B_{1}})=0}\\ \\\widehat{n}\cdot\overrightarrow{B_{2}}=\widehat{n}\cdot\overrightarrow{B_{1}} \end{}$

也就是：磁感应强度在边界上法向连续。

电场强度

分析图3.3的模型。

写出电磁感应定律的积分形式：

$\oint _{C}\overrightarrow{E}\cdot d\overrightarrow{l}=-j\omega \int _{S}\overrightarrow{B}\cdot d\overrightarrow{s}-\int _{S}\overrightarrow{M}\cdot d\overrightarrow{s}$

当回路垂直于分界面的宽边h->0的时候，回路的面积趋于0，所以第一项 $\overrightarrow{B}$ 的曲面积分可以忽略不记。

对于 $\overrightarrow{M}$ 的曲面积分，这里就有不同于《简明微波》所介绍的情况了。如果分界面存在磁流密度 $\overrightarrow{M_{S}}$ ，则 $\overrightarrow{M}$ 的表面积分的贡献可能非0（有关这块我也不是很清楚，要涉及到狄拉克函数，可能是数理方程中的知识），最后得到的应该是：

$\begin{} {\color{black} \Delta w\cdot E_{t2} - \Delta w\cdot E_{t1} = -\Delta w\cdot M_{S} }\\\\ E_{t2}-E_{t1}=-M_{S} \end{}$

向量形式则是：

$(\overrightarrow{E_{2}}-\overrightarrow{E_{1}})\times \widehat{n}=-\overrightarrow{M_{S}}$

也就是：电场强度在边界上切向连续（不考虑磁流密度时）

磁场强度

安培环路定律的积分形式：

$\oint _{C}\overrightarrow{H}\cdot d\overrightarrow{l}=j\omega \int _{S}\overrightarrow{D}\cdot d\overrightarrow{s}+\int _{S}\overrightarrow{J}\cdot d\overrightarrow{s}$

同样的分析方法，可以得到：

$\begin{} {\color{black} \Delta w\cdot H_{t2} - \Delta w\cdot H_{t1} = \Delta w\cdot J_{S} }\\\\ H_{t2}-H_{t1}=J_{S} \end{}$

矢量形式则是：

$\widehat{n}\times (\overrightarrow{E_{2}}-\overrightarrow{E_{1}})=\overrightarrow{J_{S}}$

也就是：磁场强度在边界上切向不连续，数值相差为边界上的面电流密度。

介质分界面的场

两种无耗介质分界面，通常没有电荷、电流密度、磁流密度，也就是：

$\begin{} {\color{black} \rho_{S}=0}\\ J_{S}=0\\ M_{S}=0 \end{}$

则边界条件可以简化为：

$\begin{} {\color{black} \widehat{n}\cdot (\overrightarrow{D_{2}}-\overrightarrow{D_{1}})=0}\\ \\\widehat{n}\cdot (\overrightarrow{B_{2}}-\overrightarrow{B_{1}})=0\\\\ \widehat{n}\times (\overrightarrow{E_{2}}-\overrightarrow{E_{1}})=0\\ \\\widehat{n}\times (\overrightarrow{H_{2}}-\overrightarrow{H_{1}})=0 \end{}$

穿过分界面时，D和B法向连续，E和H切向连续。

理想导体（电壁）分界面的场

对于良导体，常常假设是无耗的（σ->∞）。这种情况下，良导体内部区域所有场分量必定为0。

$\begin{} {\color{black} \widehat{n}\cdot \overrightarrow{D}=\rho_{S}}\\\\\widehat{n}\cdot \overrightarrow{B_{}}=0\\\\ \widehat{n}\times \overrightarrow{E_{}}=0(-\overrightarrow{M})\\ \\\widehat{n}\times \overrightarrow{H_{}}=\overrightarrow{J_{S}} \end{}$

同时，这也能说明为什么导体具有有限电导率，而不是门外汉认为的“导电性越好电导率就越大”。因为当电导率趋于无穷时，趋肤深度（微波功率可以穿透到达的深度）则趋于0。

磁壁边界条件

是与电壁对偶的一种情况，其中 $\overrightarrow{H}$ 切向分量必须为0。（这种边界条件实际不存在，但可以用波纹表面来近似，或者在某些平面传输线问题中用它来近似）

它的边界条件如下：

$\begin{} {\color{black} \widehat{n}\cdot \overrightarrow{D}=0}\\\\\widehat{n}\cdot \overrightarrow{B_{}}=0\\\\ \widehat{n}\times \overrightarrow{E_{}}=-\overrightarrow{M}\\ \\\widehat{n}\times \overrightarrow{H_{}}=0 \end{}$