知乎推荐,所以慕名观看,同时记录一些笔记,如果涉及到侵权等问题,直接删。
第一期:射频放大器介绍
第二期:晶体管类别;BJT晶体管
本章概括
本章内容

本章将介绍晶体管部分
晶体管类别
主要讲解蓝框中的部分——晶体管。晶体管可以分为:
- Bipolar Transistor 双极性晶体管
- BJT(Bipolar Juction Transistor 双极结型晶体管)
- HBT(Heterojunction Bipolar Transistor 异质结双极晶体管)
- Field Effect Transistor(FET)场效应晶体管
- JFET(Junction FET 结型场效应晶体管)
- MOSFET(Metal Oxide Semi-conductor FET 金属-氧化物半导体场效应晶体管)做在Silicon上,用Oxide做隔离
- MESFET(Metal Semi-conductor FET 金属-半导体场效应晶体管)
- HEMT(High Electron Mobility Transistor 高电子迁移率晶体管)
- PHEMT(Pseudomorphic HEMT)它的截面不是真正的结晶,比HEMT性能更好
BJT
硅基BJT
横截面图

- 这是一个NPN型晶体管。
- BJT有三个电极:
- 基极B(Base)
- 发射极E(Emitter)
- 集电极C(Collector)
- 橙色部分代表基极,它的长度决定了晶体管的速度(相应地,宽度决定了电流大小)。
- 蓝色部分是集电极耗尽层(depletion layer),在这里带电载流子密度很低(因为是电子和空穴结合的区域)。
- P和N区之间会形成一个Junction(在图中是E级那边包着的一个镂空梯形,画了阴影线),中间有等效电容
C
b
e
C_{be}
Cbe。
C
b
e
C_{be}
Cbe是一个扩散电容,只是具有电容效应,不是真正存在的电容。
C
b
e
C_{be}
Cbe的表明能量的传递不完全依靠电子的移动,能量可以直接通过电容“漏”过去——位移电流。
公式: C b e = τ b g m C_{be}=\tau_b g_m Cbe=τbgm
其中 τ b \tau_b τb是电子在基极移动时的delaytime延迟时间, g m = 1 r e g_m=\frac{1}{r_e} gm=re1
所以也能写成: r e ⋅ C b e = τ b r_e\cdot C_{be}=\tau_b re⋅Cbe=τb(电容的时间常数公式)
这个公式就是用RC回路来模拟电子的延迟时间(和第三点对应,如果基极长度小,这个 τ b \tau_b τb会小,速度就越快) - b − e b-e b−e间的电流是 b − b ′ b-b^{'} b−b′间的电流的 1 + h f 1 1+hf1 1+hf1倍(我没听清楚这个“hf1”到底是怎么拼的,凑合一下。这东西基本就是模电的放大倍数)。如果扩散电容 C b e C_{be} Cbe漏电就会使射级损失很多电流。
- 电子要从N区进入P区,要有一个能级的跃迁,这一部分能量的消耗被等效为一个小电阻 r e r_e re(图中看起来是和等效电容并联着的)。
- 左侧电阻 r b b ′ r_{bb^{'}} rbb′是因为电子在移动时能量会持续地损失。真正的基极到
- C b c C_{bc} Cbc是真正的电容,是由于夹层而构成的电容。
- 最下层是集电极衬底(Collector Substrate),他最终能吸收来的电流并不是完全的 i e i_{e} ie, i e i_{e} ie有一部分漏到基极去了,所以集电极接受的电流是 α i e \alpha i_{e} αie(模电里面提过的 α \alpha α和 β \beta β两个系数,微波里喜欢用 α \alpha α, α < 1 \alpha<1 α<1)
俯视图

(能看到EB。C在底下看不到)
发射极伸入基极的部分,通过Emitter Width射级宽度和Emitter Periphery射级外围(也就是长度)形成了一个面积,这个面积决定了电流的大小。一般晶体管会给出多少电流每平方微米,单位是: m A / u m 2 mA/um^{2} mA/um2(就是电流密度)。
往往要让功率大,效率高,就要让电流密度大;要让电流密度大,就要让有效面积大。
这一张图其实是两个管子并联:
 工程中要做到电流大,采用的是多个管子并联: 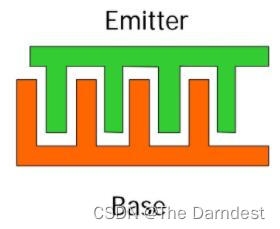 而不是一下子把面积做得很大,电流会不均匀。
工程中要做到电流大,采用的是多个管子并联:  而不是一下子把面积做得很大,电流会不均匀。
封装示意图
 教授举例了一些封装。 其中有的封装有多个Emitter引脚,弹幕说是一根射级不够走大电流。 并且如果是很大的级(就是字面意思,看上去很大),那一定是Emitter。
教授举例了一些封装。 其中有的封装有多个Emitter引脚,弹幕说是一根射级不够走大电流。 并且如果是很大的级(就是字面意思,看上去很大),那一定是Emitter。
注意图中最上面红色的,是一种常见的封装。

平面朝自己,引脚依次是EBC。(美规的是这样的,日规的不太一样是ECB)
HBT

主要构成
这是一个“砷化镓”或“砷化铝镓”的异质结双极型晶体管(PNP)。它的极都是金属制的。其中基极做了对称,是为了便于并联使用。
射级与基板之间有一块相对突出的材料,被叫做 E m i t t e r M e s a Emitter\;Mesa EmitterMesa,即:“发射极台面”。这块 n + n^+ n+性的材料是 A l G a A s AlGaAs AlGaAs; p p p性的基极材料使用的是 G a A s GaAs GaAs。它们之间形成了一个接面,称为
A l G a A s / G a A s H e t e r o j u n c t i o n AlGaAs/GaAs\;Heterojunction AlGaAs/GaAsHeterojunction 砷化铝镓/砷化镓异质结
最后的基底是半绝缘砷化镓基底。
制作方法
可以看到 l a y e r layer layer都是一层接一层的,采用的是蚀刻的制作工艺。
HBT的制作精度要求很高,中间的层厚度要控制的很精确;同时由于 G a A s GaAs GaAs等原料也更贵,所以HBT要比BJT贵很多。(但我不知道现在怎么样了)
常用材料组合
| 射级(Emitter)材料( n + n^+ n+) | 基极(Base)材料( p p p) | 衬底(Substrate)材料 |
|---|---|---|
| A l G a A s AlGaAs AlGaAs | G a A s GaAs GaAs | G a A s GaAs GaAs |
| I n A l A s InAlAs InAlAs | I n G a A s InGaAs InGaAs | I n G a A s InGaAs InGaAs |
| I n G a P \color{red}{InGaP} InGaP | G a A s \color{red}{GaAs} GaAs | G a A s \color{red}{GaAs} GaAs |
| S i \color{blue}{Si} Si | S i G e \color{blue}{SiGe} SiGe | S i G e \color{blue}{SiGe} SiGe |
其中,第三行标红的是应用最广泛的;第四行标蓝的组合性能也不错,价钱也稍微低一些。
MMIC布局

- (Emitter contact)最中间的是金属材质的电极;
- (Emitter mesa)射级电极紧贴着射级台面;
- (Base pedestal)射级台面长在基极基板上;
- (Base contact)同时基极电极也在基极基板上;
- (Collector contact)集电极电极独立于基极基板;
- (Isolation implant)最终所有东西都要被隔离外围隔离起来(用粒子把晶格破坏使其丧失导电性——就是前一张图中的Implantation damage离子注入损伤)
教授顺便提到说substrate最好也是绝缘的。如果它导电,有电阻,是lossy的,电磁波通过它被吸收消耗掉,损失功率。不过往往在生产中不做绝缘的,成本很高(田教授经典结论:老板不乐意)。
HBT vs Si BJT
-
相同点:都是纵向电流,且是双载流子(电子、空穴)。
-
不同点 BJT HBT 分析 BE接面 同质(Silicon) 异质 基极掺杂 5 × 1 0 8 c m − 3 5\times10^8\;cm^{-3} 5×108cm−3 > 4 × 1 0 9 c m − 3 >4\times10^9\;cm^{-3} >4×109cm−3 r b ′ e o r r e r_{b^{'}e}\;or\;r_{e} rb′eorre U T i b ( 常温下百 Ω 级 ) o r U T i e ( 常温下 Ω 级 ) \frac{U_T}{i_b}(常温下百\Omega级)\;or\;\frac{U_T}{i_e}(常温下\Omega级) ibUT(常温下百Ω级)orieUT(常温下Ω级) l o w e r lower lower 掺杂高,能障低,速度快 v s a t ( e − ) v_{sat}(e^-) vsat(e−)(电子饱和速度) 0.7 × 1 0 7 c m / s 0.7\times10^7\;cm/s 0.7×107cm/s > 2 × 1 0 7 c m / s >2\times10^7\;cm/s >2×107cm/s HBT3倍左右,更快 G a i n ( g m ) Gain(g_m) Gain(gm) i c U T \frac{i_c}{U_T} UTic h i g h e r higher higher HBT高增益更适合功放 基极厚度 0.1 μ m 0.1 \mu m 0.1μm(对BJT来说能障高,厚度再降收益也不高) 0.06 μ m 0.06\mu m 0.06μm 基极厚度越薄速度越快 f T f_T\; fT(电流增益降至1的频率) f T = g m 2 π C b ′ e f_T=\frac{g_m}{2\pi C_{b^{'}e}} fT=2πCb′egm h i g h e r higher higher Substrate 基板材料 L o s s y (阻性 = 有损耗) Lossy(阻性=有损耗) Lossy(阻性=有损耗) H i g h r e s i s t a n c e (高阻 = 不导电) High\;resistance(高阻=不导电) Highresistance(高阻=不导电) HBT没有导电损耗
小信号模型
在RF电路中,任何一个Bipolar Transistor都是将电压转换成电流的器件(模电中可以说成是电流放大)。
在RF中,主要使用 g m g_m gm,也就是模电中提到的“跨导”。注意这种小信号模型参数其实并不是常数,是随着偏置( i c , U c e i_c,U_{ce} ic,Uce)改变的(Bias Depended)。
由于小信号相对于直流偏置很小,所以加小信号后工作点“感觉没有变化”,才可以独立出直流偏置电路,通过偏置电路给出这些参数,再去计算交流通路。

如果无情一点,管子的模型是…

上文提到随偏置改变的主要就是橙色圈内的参数—— I n t r i n s i c m o d e l Intrinsic\;model Intrinsicmodel
随后,外部的封装难免会出现寄生的电感、电阻、电容成分,形成外部结构模型—— E x t r i n s i c m o d e l Extrinsic\;model Extrinsicmodel。封装是固定的,所以这些参数在封装时就确定不变化。

然后经过了奇奇怪怪的标注以后,这个图成了这个样子…大致重要的都在图中被标记了,这里就不多讲了。
其中的
α
\alpha
α在上一期提到过,但是没多讲。和模电定义一致,它的公式是:
α
=
h
f
e
1
+
h
f
e
,
h
f
e
就是指的
β
(2.1)
\alpha=\frac{hfe}{1+hfe},\;\; hfe就是指的\beta\tag{2.1}
α=1+hfehfe,hfe就是指的β(2.1)
并且在这里它是一个频率相关的函数:
α
=
A
(
f
)
\alpha=A(f)
α=A(f)。
大信号模型

教授说学微波的一定要了解。另外,专门讲模型的书可能会用三四十种公式来模拟所有的元件值(太可怕了),所有都随偏压而变。
混合 π \pi π模型(简化的)

- r b b ′ r_{bb^{'}} rbb′:基极金属电极到真正基极之间的电阻;
- r b ′ e r_{b^{'}e} rb′e:能级障碍等效的电阻;
- C b ′ e C_{b^{'}e} Cb′e:扩散电容,反映电子从射级到基极所需的时间 τ = C b ′ e ⋅ r e \tau=C_{b^{'}e}\cdot r_{e} τ=Cb′e⋅re(并不是和扩散电容并联的这个 r b ′ e r_{b^{'}e} rb′e!);
- C b ′ c C_{b^{'}c} Cb′c:基极和集电极之间真实的电容
- g m U b ′ e g_mU_{b^{'}e} gmUb′e:压控电流源转移函数,主要体现电压到电流的转换。
在这个模型里,所有的参数包括放大倍数都会随着直流偏置而变。如果是功放等有大交流信号成分,也会随着交流信号而变。本质上这个模型也是小信号模型,信号过大应该换用大信号模型。
H参数
“混合”一词的英文是 H y b r i d Hybrid Hybrid,相对应地,在混合 π \pi π模型中存在一个 [ h ] [h] [h]参数矩阵。

放大系数
h
f
e
hfe
hfe就是其中的
h
21
h_{21}
h21,物理含义是当
V
2
=
0
V_2=0
V2=0也就是输出短路时,输出电流与输入电流之比:
h
f
e
=
h
21
=
I
2
I
1
∣
V
2
=
0
(2.2)
hfe=h_{21}=\frac{I_2}{I_1}|_{V_2=0}\tag{2.2}
hfe=h21=I1I2∣V2=0(2.2)
h
f
e
hfe
hfe还有一个叫法是:“短路电流增益”。

从 r b b ′ r_{bb^{'}} rbb′过去的电流 i b i_b ib,大部分经过了 r b ′ e r_{b^{'}e} rb′e,记为 i b ′ i_b^{'} ib′。只有 i b ′ i_b^{'} ib′这一部分被放大,以 h f e D C ⋅ i b ′ hfe_{DC}\cdot i_b^{'} hfeDC⋅ib′的数值从集电极输出(这是用用电容来模拟放大倍数的频率变化,所以放大倍数是直流放大倍数;如果让放大倍数本身是频率的函数,这里就可以直接用 i b i_b ib)。
图中蓝色部分,电容(由于输出短路接地所以 C b ′ c C_{b^{'}c} Cb′c和 C b ′ e C_{b^{'}e} Cb′e就构成了并联关系,电容并联容值相加)会造成电流的泄露,这一部分没有被放大,直接流掉了。

所以 h f e = h f e ( f ) h_{fe}=h_{fe}(f) hfe=hfe(f)随频率递减变化。
封装模型

上图是一个封装模型。中间圈起来的BJT已在前面解释,我们关注的是外面的部分。
首先在三个电极两两之间都会有寄生电容(我觉得图中 n 1 , n 2 , n 3 n_1,n_2,n_3 n1,n2,n3三个点是引出来使用户接线的金属电极,真正的EBC是圈内的,所以应该是管子极间电容)。
其次是三段传输线。 T R L TRL TRL,代表 T r a n s m i s s i o n l i n e Transmission\;line Transmissionline即传输线模型。如果传输线长 l < 1 20 λ l<\frac{1}{20}\lambda l<201λ则可以画成:

如果 > 1 20 λ >\frac{1}{20}\lambda >201λ就只能用 T R L TRL TRL表示。
转移特性
在分析直流偏执特性前,先插入这一部分,主要是需要用到 I c I_c Ic公式。
I c − U b e I_c-U_{be} Ic−Ube曲线:

注意在这里我找了一张 I b − U b e I_b-U_{be} Ib−Ube的曲线,并不是所要说的。但是没关系,假定放大倍数确定,也就是简单的倍率关系。
言归正传,
I
c
−
U
b
e
I_c-U_{be}
Ic−Ube曲线,也就是输出电流-输入电压的转移特性曲线。它的关系如下:
I
c
=
f
(
u
b
e
)
≈
I
e
=
I
s
(
e
u
b
e
U
T
−
1
)
(2.3)
I_c=f(u_{be})\approx I_e=I_s(e^{\frac{u_{be}}{U_T}}-1)\tag{2.3}
Ic=f(ube)≈Ie=Is(eUTube−1)(2.3)
这样是最简单的形式。考虑到各种因素,写成这样样子才全面:
I
c
=
f
(
u
b
e
)
≈
I
e
=
I
s
(
e
u
b
e
n
U
T
−
1
)
,
n
代表修正因子
(2.4)
I_c=f(u_{be})\approx I_e=I_s(e^{\frac{u_{be}}{{\color{red}{n}}U_T}}-1),\;\;\;\;n代表修正因子\tag{2.4}
Ic=f(ube)≈Ie=Is(enUTube−1),n代表修正因子(2.4)
DC偏置特性

我将两张图片结合起来。左图是仿真做的图;右图是平时讲解管子特性时使用的输出特性曲线图。反映的是同样的东西。
h f e = I c I b hfe=\frac{I_c}{I_b} hfe=IbIc是电流放大倍数。交流信号使用电压->电流的跨导 g m = ∂ I c ∂ U b e g_m=\frac{\partial I_c}{\partial U_{be}} gm=∂Ube∂Ic。
放大倍数大小判断
如果要比较放大倍数,应该分析跨导公式。不过跨导公式的两个变量在此图中不能一下子看出来。
g
m
=
∂
I
c
∂
U
b
e
=
∂
[
I
s
(
e
u
b
e
U
T
−
1
)
]
∂
u
b
e
=
I
s
U
T
(
e
u
b
e
U
T
−
1
)
=
I
c
U
T
(2.5)
g_m=\frac{\partial I_c}{\partial U_{be}}=\frac{\partial [I_s(e^{\frac{u_{be}}{U_T}}-1)]}{\partial u_ {be}}=\frac{I_s}{U_T}(e^{\frac{u_{be}}{U_T}}-1)=\frac{I_c}{U_T}\tag{2.5}
gm=∂Ube∂Ic=∂ube∂[Is(eUTube−1)]=UTIs(eUTube−1)=UTIc(2.5)
所以在放大区内,
I
c
I_c
Ic大,放大倍数就大!
CE间模拟的大电阻 r o r_o ro

我们会发现,右图作为定性分析的简图,在放大区, I c I_c Ic就几乎不随 I b I_b Ib变化,完全是平行横轴的曲线。但实际上,左图可以看出, I c I_c Ic即便在放大区也是在变化的。而这也体现在小信号模型( π \pi π模型)中在 C E CE CE两极之间的电阻 r o r_o ro。
这个电阻的定义是: r o = ∂ U b e ∂ I c r_o=\frac{\partial U_{be}}{\partial I_{c}} ro=∂Ic∂Ube。
它的大小可以这样估计:在曲线的放大区中,取一小段 Δ U c e \Delta U_{ce} ΔUce(橙色双线),及其所对应的 Δ I c \Delta I_c ΔIc(红色双线),可以发现前者相对于后者是很大的,所以** r o r_o ro很大**,在模电(应该在模电里写作 r c e r_{ce} rce 吧)分析的时候常将其视作高阻短路。
简单来说,这个电阻就是用来模拟曲线的轻微倾斜而引入的,模电将其忽略就是代表简化倾斜曲线为平坦曲线了。
放大特性
直流偏置主要指的是 I C Q I_{CQ} ICQ和 U C E Q U_{CEQ} UCEQ,也就是不加交流时的 I C I_C IC和 U C E U_{CE} UCE。通过这两个值定位管子处于输出特性曲线中什么区域,然后再分析交流特性。
不论是模电中的电流放大,还是微波中的电压-电流信号转换,电流总归是输出。这个输出电流就是 I C I_C IC,控制输出电流的控制电压是 U B E U_{BE} UBE( U C E U_{CE} UCE是输出电压,不是控制电压)。

上图就是晶体管输出图解。其核心是
I
C
I_C
IC的转移特性曲线,不同的是加入了交流小信号——而交流小信号是直接加在控制电压
U
B
E
U_{BE}
UBE上的。用公式来说明:如果
E
m
i
t
t
e
r
Emitter
Emitter接地,则控制电压的大小如下——
U
B
E
=
U
B
B
+
u
−
U
B
E
(
O
N
)
U
B
B
代表基极电压,
u
代表交流信号,
U
B
E
(
O
N
)
为管压降
(2.6)
U_{BE}=U_{BB}+u-U_{BE(ON)}\\U_{BB}代表基极电压,u代表交流信号,U_{BE(ON)}为管压降\tag{2.6}
UBE=UBB+u−UBE(ON)UBB代表基极电压,u代表交流信号,UBE(ON)为管压降(2.6)
控制电压
U
B
E
U_{BE}
UBE和输出电流
I
C
I_C
IC又通过关系式
I
C
=
I
s
(
e
u
b
e
U
T
−
1
)
I_C=I_s(e^{\frac{u_{be}}{U_T}}-1)
IC=Is(eUTube−1) 关联,由此,
I
C
I_C
IC也会相应波动。
*注意这种波动并非完美的余弦,由于关系式的指数特性, I C I_C IC的“余弦”是上凸高度大于下凹深度的。
*补充一点,跨导 g m g_m gm是可以通过曲线的切线斜率来计算,公式仍就是上面那个,但是也不一定要化简成 g m = I C U T g_m=\frac{I_C}{U_T} gm=UTIC,只要知道 I C Q I_{CQ} ICQ对应那点(中心点)在知道一个挨得很近的点,利用两点法求个斜率就行(不精确但是很快)。
低通特性(整节中应该以“频率特性”为题)
3 d B 3dB 3dB截止频率 f β f_\beta fβ
由上面的分析可以知道,输出电流可以写为: I C = h f e D C ⋅ i b ′ I_C=hfe_{DC}\cdot i^{'}_b IC=hfeDC⋅ib′ 或者 I C = h f e ( f ) ⋅ i b I_C=hfe(f)\cdot i_b IC=hfe(f)⋅ib。
假设输入一定频率的信号,那么电流的分流关系可以用导纳来表示,可以写出:
i
b
′
=
i
b
⋅
1
r
b
′
e
1
r
b
′
e
+
j
ω
(
C
b
′
c
+
C
b
′
e
)
(2.7)
i^{'}_b=i_b\cdot \frac{\frac{1}{r_{b^{'}e}}}{\frac{1}{r_{b^{'}e}}+j\omega (C_{b^{'}c}+C_{b^{'}e})}\tag{2.7}
ib′=ib⋅rb′e1+jω(Cb′c+Cb′e)rb′e1(2.7)
因此,得到:
h
f
e
(
f
)
=
1
r
b
′
e
1
r
b
′
e
+
j
ω
(
C
b
′
c
+
C
b
′
e
)
⋅
h
f
e
D
C
=
1
1
+
j
f
f
β
⋅
h
f
e
D
C
,
其中
f
β
=
1
2
π
(
C
b
′
c
+
C
b
′
e
)
r
b
′
e
:
3
d
B
截止频率
(2.7)
hfe(f)=\frac{\frac{1}{r_{b^{'}e}}}{\frac{1}{r_{b^{'}e}}+j\omega (C_{b^{'}c}+C_{b^{'}e})}\cdot hfe_{DC}=\frac{1}{1+j\frac{f}{f_\beta}}\cdot hfe_{DC},\;\;\;\;\\其中f_\beta=\frac{1}{2\pi(C_{b^{'}c}+C_{b^{'}e})r_{b^{'}e}}:3dB截止频率\tag{2.7}
hfe(f)=rb′e1+jω(Cb′c+Cb′e)rb′e1⋅hfeDC=1+jfβf1⋅hfeDC,其中fβ=2π(Cb′c+Cb′e)rb′e1:3dB截止频率(2.7)
当
f
=
f
β
f=f_\beta
f=fβ时,说明
h
f
e
hfe
hfe已经比
h
f
e
D
C
hfe_{DC}
hfeDC掉
3
d
B
3dB
3dB(
h
f
e
(
f
β
)
=
1
1
+
j
h
f
e
D
C
hfe(f_\beta)=\frac{1}{1+j}hfe_{DC}
hfe(fβ)=1+j1hfeDC)了。掉
3
d
B
3dB
3dB也就意味着输出电流变成了理想的
1
2
\frac{1}{\sqrt{2}}
21,功率就变成了
1
2
\frac{1}{2}
21。
所以晶体管就构成了一个低通电路(RC回路),频率低放大特性好,频率高就寄寄啦!
转换频率 f T f_T fT(忘了模电的叫法了)
它是叫做:Transition frequency。
当 f = f T f=f_T f=fT时, h f e ( f T ) = 1 hfe(f_T)=1 hfe(fT)=1。
可以计算出此时(忽略掉分母的”+1“):
f
T
=
h
f
e
D
C
×
f
β
=
g
m
2
π
(
C
b
′
c
+
C
b
′
e
)
(2.8)
f_T=hfe_{DC}\times f_\beta=\frac{g_m}{2\pi(C_{b^{'}c}+C_{b^{'}e})}\tag{2.8}
fT=hfeDC×fβ=2π(Cb′c+Cb′e)gm(2.8)
电子通过能障的时间
f T = g m 2 π ( C b ′ c + C b ′ e ) = 1 2 π τ e c = 2 μ n U T 2 π W b 2 τ e c = C Σ g m ,此处 τ e c = τ e b ′ + τ b ′ c ,是电子从射级到基极,再从基极到集电极的时间。 (2.9) f_T=\frac{g_m}{2\pi(C_{b^{'}c}+C_{b^{'}e})}=\frac{1}{2\pi\tau_{ec}}=\frac{2\mu_nU_T}{2\pi W_b^2}\tag{2.9}\\ \tau_{ec}=\frac{C_\Sigma}{g_m},此处\tau_{ec}=\tau_{eb^{'}}+\tau_{b^{'}c},是电子从射级到基极,再从基极到集电极的时间。 fT=2π(Cb′c+Cb′e)gm=2πτec1=2πWb22μnUTτec=gmCΣ,此处τec=τeb′+τb′c,是电子从射级到基极,再从基极到集电极的时间。(2.9)
转换频率越高,就意味着电子跨越基极-射级能障的时间越短,响应速度越快。
由于 C b ′ e > C b ′ c C_{b^{'}e}>C_{b^{'}c} Cb′e>Cb′c,所以 τ b ′ e > τ b ′ c \tau_{b^{'}e}>\tau_{b^{'}c} τb′e>τb′c,电子穿过能障消耗的时间主要在be之间。
式最后一部分:
f
T
=
2
μ
n
V
T
2
π
W
b
2
μ
n
:电子移动率
V
T
:电子运动速度
W
b
:基极厚度
(2.10)
f_T=\frac{2\mu_nV_T}{2\pi W_b^2}\tag{2.10}\\ \mu_n:电子移动率\\ V_T:电子运动速度\\ W_b:基极厚度
fT=2πWb22μnVTμn:电子移动率VT:电子运动速度Wb:基极厚度(2.10)
可以通过HBTvsBJT的表格来判断HBT和BJT的性能差异。
实际上 τ e c \tau_{ec} τec这个时间写完整是很复杂的:
 $$ \begin{aligned} \tau_{ec}&=\tau_e(穿过射极材料所需时间)\\ &+\tau_{eb}(跨过射级和基极间能障所需时间,最大)\\ &+\tau_b(穿过基极材料所需时间)\\ &+\tau_{bc}(跨过基极和集电极能障所需时间)\\ &+\tau_{d}(跨过depletion\;layer耗尽层所需时间)\\ &+\tau_c(穿过集电极基板所需时间) \end{aligned}\tag{2.11} $$
$$ \begin{aligned} \tau_{ec}&=\tau_e(穿过射极材料所需时间)\\ &+\tau_{eb}(跨过射级和基极间能障所需时间,最大)\\ &+\tau_b(穿过基极材料所需时间)\\ &+\tau_{bc}(跨过基极和集电极能障所需时间)\\ &+\tau_{d}(跨过depletion\;layer耗尽层所需时间)\\ &+\tau_c(穿过集电极基板所需时间) \end{aligned}\tag{2.11} $$
波特图
波特图可以反映放大倍数随着频率的对数变化情况。

-
当 f < f β f<f_\beta f<fβ时,放大倍数几乎没有变化,都可以近似为 h f e ( f ) = h f e D C hfe(f)=hfe_{DC} hfe(f)=hfeDC;
-
在 f → f β f\rightarrow f_\beta f→fβ时,曲线略微下降,放大倍数开始降低;
-
当 f = f β f=f_\beta f=fβ时, h f e ( f ) = 1 2 h f e D C hfe(f)=\frac{1}{\sqrt{2}}hfe_{DC} hfe(f)=21hfeDC,在对数上是 − 3 d B ( − 3 d B = 20 l o g ( 0.707 ) ) {\color{red}{-3dB}}(-3dB=20log(0.707)) −3dB(−3dB=20log(0.707)),在功率上是 1 2 \frac{1}{2} 21;
-
当 f β < f < f T f_\beta<f<f_T fβ<f<fT时,稍微靠后有一段较直的倾斜线段,此处:
-
− 20 d B / d e c a d e -20dB/decade −20dB/decade
频率每提升 10 d B (变为 10 倍) {\color{red}{10dB}}(变为10倍) 10dB(变为10倍)
h f e hfe hfe就下降 20 d B (根据式 2.7 , h f e 真值变为 1 10 ,故 − 20 d B = 20 l o g ( 1 10 ) ) {\color{red}{20dB}}(根据式2.7,hfe真值变为\frac{1}{10},故-20dB=20log(\frac{1}{10})) 20dB(根据式2.7,hfe真值变为101,故−20dB=20log(101));
-
− 6 d B / o c t a v e -6dB/octave −6dB/octave(乐理中的八度)
频率每提升 3 d B (变为 2 倍) {\color{red}{3dB}}(变为2倍) 3dB(变为2倍)
h f e hfe hfe就下降 6 d B (根据式 2.7 , h f e 真值变为 1 2 ,故 − 6 d B = 20 l o g ( 1 2 ) ) {\color{red}{6dB}}(根据式2.7,hfe真值变为\frac{1}{2},故-6dB=20log(\frac{1}{2})) 6dB(根据式2.7,hfe真值变为21,故−6dB=20log(21));
-
-
当 f = f T f=f_T f=fT时,放大倍数 h f e = 0 d B = 1 hfe=0dB=1 hfe=0dB=1。
例子
比如已知 f = 300 M H z f=300MHz f=300MHz时 h f e = 10 d B hfe=10dB hfe=10dB,那么可以很容易得到 f T = f × 1 0 ( 10 / 10 ) × 1 2 = 300 M H z × 3.162 = 948.6 M H z f_T=f\times10^{(10/10)\times\frac{1}{2}}=300MHz\times3.162=948.6MHz fT=f×10(10/10)×21=300MHz×3.162=948.6MHz。
Miller效应
之前讨论的都是在输出短路情况下。如果负载接正电阻,则会引发 M i l l e r 效应 Miller效应 Miller效应。随着负载电阻增加,等效寄生电容增加, f β 、 f T f_\beta、f_T fβ、fT都会下降。
























 4534
4534

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








