Deep Learning：正则化（十二）

Dropout

Dropout (Srivastava et al., 2014) provides a computationally inexpensive but powerful method of regularizing a broad family of models.
To a first approximation, dropout can be thought of as a method of making bagging practical for ensembles of very many large neural networks. Bagging involves training multiple models, and evaluating multiple models on each test example. This seems impractical when each model is a large neural network, since training and evaluating such networks is costly in terms of runtime and memory.
Dropout provides an inexpensive approximation to training and evaluating a bagged ensemble of exponentially many neural networks.
Specifically, dropout trains the ensemble consisting of all sub-networks that can be formed by removing non-output units from an underlying base network:

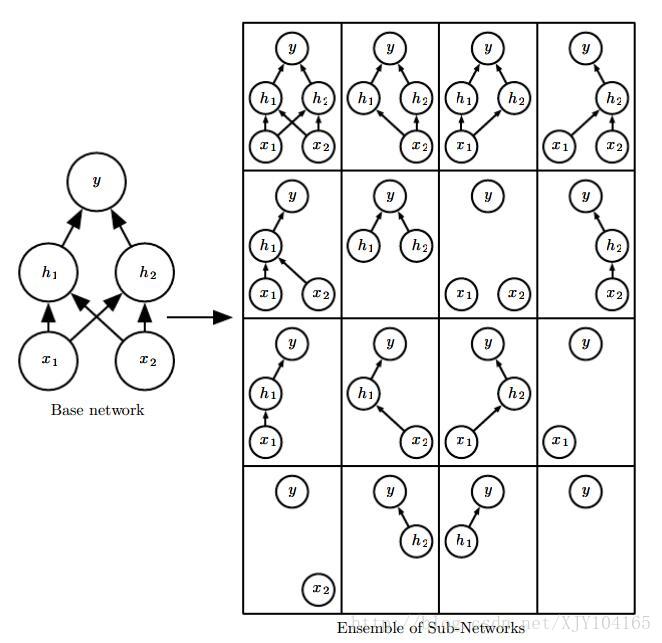
Recall that to learn with bagging, we define k different models, construct k different datasets by sampling from the training set with replacement, and then train model i on dataset i. Dropout aims to approximate this process, but with an exponentially large number of neural networks.
Specifically, to train with dropout, we use a minibatch-based learning algorithm that makes small steps, such as stochastic gradient descent.

• Each time we load an example into a minibatch, we randomly sample a different binary mask to apply to all of the input and hidden units in the network.
• The mask for each unit is sampled independently from all of the others. The probability of sampling a mask value of one (causing a unit to be included) is a hyperparameter fixed before training begins.
• Typically, an input unit is included with probability 0.8 and a hidden unit is included with
  probability 0.5. We then run forward propagation, back-propagation, and the learning update as usual.
• Dropout training is not quite the same as bagging training.
  (1) In the case of bagging, the models are all independent. In the case of dropout, the models share parameters, with each model inheriting a different subset of parameters from the parent neural network.
  (2) In the case of bagging, each model is trained to convergence on its respective training set. In the case of dropout, typically most models are not explicitly trained at all—usually, the model is large enough that it would be infeasible to sample all possible subnetworks within the lifetime of the universe. Instead, a tiny fraction of the possible sub-networks are each trained for a single step, and the parameter sharing causes the remaining sub-networks to arrive at good settings of the parameters.