计算机视觉 单应性 Homography

该博客内容发表在泡泡机器人公众号上，请尊重泡泡机器人公众号的版权声明

在ORB-SLAM初始化的时候，作者提到，如果场景是平面，或者近似平面，或者低视差时，我们能应用单应性矩阵(homography)，这三种情形在我应用SVO的过程中颇有同感，打破了我对 H 矩阵的固有映像，即只能用于平面或近似平面。但是我不知道如何去具体分析这里面的误差，比如不共面的情况时，应用 H 矩阵将一个图像坐标从图像1投影到图像2时，它会落在图像哪个位置？和实际位置的误差该怎么计算？误差会有多大？和哪些因素有关？另外，为何相机只做纯旋转运动时，不管平面还是非平面， H 矩阵都能应用？等等，一些列问题，让我感觉对homography了解很粗浅。

先简单回顾我脑海里的 H 矩阵，让大家有点代入感，原谅我的啰嗦，进入正文以后就会尽量言简意赅。在没做视觉SLAM以前，通过opencv大概知道：利用两个图像中至少四个特征点能够求解一个单应性矩阵(homography matrix)，然后用这个单应性矩阵 H 能够将图像1中的某个坐标 (u,v) 变换到图像2中对应的位置 (u′,v′) 。然而，那时忽略了两个图像能够计算 H 的前提条件。在学SLAM过程中，知道 H 矩阵的推导是来自于相机在不同位姿拍摄同一个三维平面，所以使用opencv计算单应性矩阵 H 的时候前提是两个图像对应区域必须是同一平面。

最近，刘浩敏师兄的RKSLAM里面用了多 H 矩阵来提高鲁棒性，以及加上开头的那些疑问让我有迫切进一步学习 H 矩阵的想法。本文将包括三部分： H 的由来， H 矩阵的扩展：相机的纯旋转和非共面情形，由 H 矩阵到6点法估计本征矩阵 E 。

H 矩阵的由来

假设相机在两个不同位姿处拍摄一个平面，该平面在frame 1中的法向量为 N ，到frame 1原点距离为 d ，具体如下图所示

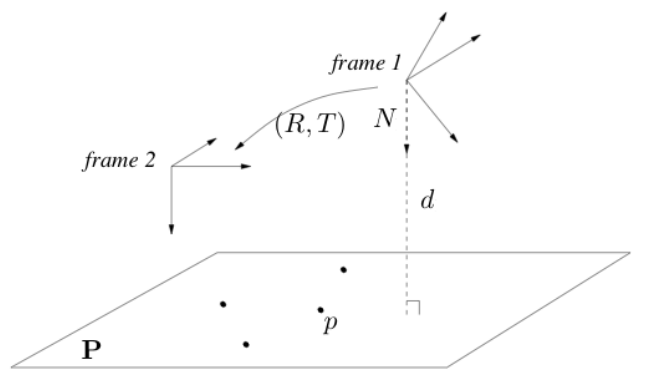
于是，坐标系1中的点可以用下式转换到坐标系2中：

X2=RX1+T

注意， 大写粗体 X 表示的是 三维空间点。同时，由于三维点 X1 所在平面上，由简单的直角三角形，可知该点沿着法线方向的投影距离应等于 d ：

NTX1=n1X+n2Y+n3Z=d

或者

1dNTX1=1∀X1∈P

结合起来我们能够得到：

X2=RX1+T1dNTX1=HX1

所以我们就得到了平面单应性矩阵

H=R+T1dNT,H∈R3×3

回忆之前提到过本征矩阵 xT2Ex1=xT2T^Rx1=0 ，它只是把点对应到一条极线，而 单应性矩阵约束更强，是点到点的一一对应。

注意，本征矩阵约束公式是对于归一化图像平面坐标 x=(x,y,1)T 而言的，而上述推导的 H 是对三维空间点的。从3d到2d, 只需要将3d点向归一化图像平面 z=1 上投影。三维空间点到归一化图像平面只是对坐标缩放了 z ，有：

λ1x1=X1,λ2x2=X2→λ2x2=Hλ1x1

从这里我们可以发现，从归一化图像平面坐标 x2 到 Hx1 之间还存在一个尺度因子，因此我们利用两个图像对应的坐标对能恢复 H ，但从该 H 中无法将平移 T 和 d 分离出来，就导致了尺度的不确定性。而利用 H ，我们能得到 x2∼Hx1 ，注意虽然这里是用的相似符号，但是我们还是能得到图像坐标的一一对应，计算出 x=Hx1 以后，将 x 的坐标都除以 xz 进行坐标归一化，就能得到 x2 。

H矩阵的扩展：相机的纯旋转和非共面情形

先看纯旋转情形，三维坐标关系如下：

X2=RX1

对应的有

H=R+T1dNT,T=0

我们可以发现公式H和深度d没有关系了，无论三维点是否在一个平面上， H 矩阵都能完美的符合他们之前的转换关系。同时，平移向量为0，可以等价于所有点位于无穷远平面上，即 d←∞ 。从另一个角度来看，如果位移为0，也无法计算d，d为任意值都能满足上面点的转换关系。所以， 大家在做全景拼接的时候，要尽量只用纯旋转哦！当然，如果相机全景拼接算法好，就当我没说。
好了，让我们回到另一个问题，即非共面情形，又不是纯旋转，那我们使用一个 H 矩阵来进行坐标点的转换误差会咋样?

假设我们有一些非共面点，通过RANSAC算法估计了一个满足大多数点对应关系的 H 矩阵，那么对于不在三维平面上的 p′ 用矩阵 H 转换以后， H 会强迫它落到三维平面上，然后投影到另一个图像归一化平面，示意图如下：

也就是说 p′ 实际应该对应 x′2 ，由于使用了错误的模型 H ，它会落到 x2 。 x2 的横纵坐标通过H矩阵能够算出， x′2 坐标通过将 p′ 进行旋转矩阵 R 和平移 T ，再投影以后也能算出。因此两个坐标相减就能得到误差模型。不需要精确的数学计算，单单从上面的图，我们就能直观的感受到 当相机的平移向量相对于场景深度而言足够小时， x′2 和 x2 之间的误差是可被接受的，即这种情况下依然可以使用H矩阵来算坐标的一一对应，这应该就是orbslam中提到的低视差情形。

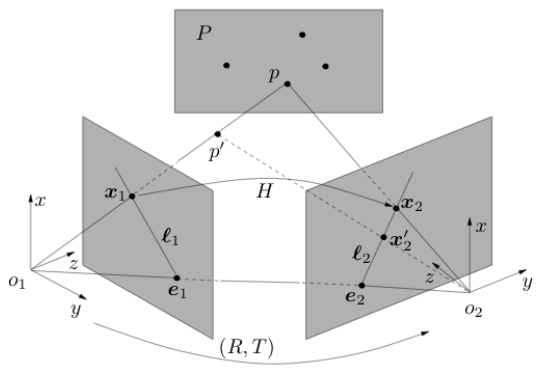
一个重要的启示是： H 矩阵的这种直接计算图像坐标一一对应关系的性质给解决SLAM中像素点的匹配又提供了一条思路，如果一个 H 矩阵不行，那一幅图片就用多个 H 矩阵，这正是浩敏师兄那篇ISMAR 2016论文的重要框架基础。而通过本征矩阵 E 只能计算极线，还需要沿着极线匹配。

由 H 矩阵到本征矩阵 E 的一点遐想

既然说到了极线，顺着上面的思路，干脆探一探本征矩阵 E 。其实，上面图中，大家伙都看到 x′2 和 x2 是位于极线上的，他们坐标都知道，就能得到极线方程，如果还有另外一个点再确定一条极线，如下图所示

那么外极点 e2 就能确定，极点确定了，H也知道，那么其他任意点的极线就能画出来了，不用本征矩阵我们也可以构造极线几何。这就是所谓的“六点法”，四个共面点确定H,两个非共面点确定极点。

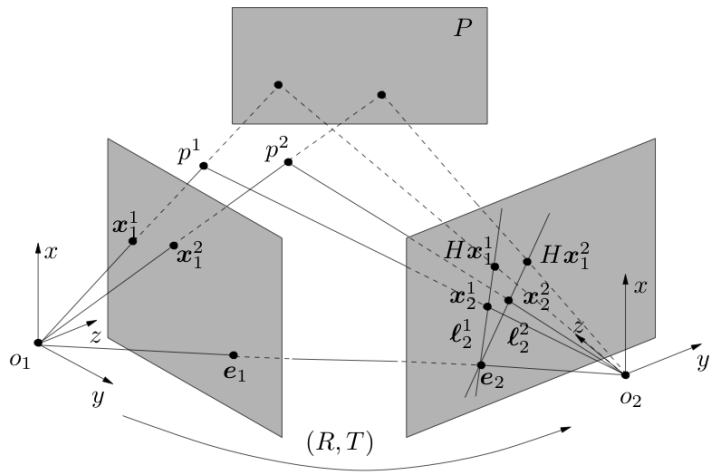
另外，还可以解释为什么8点法计算求解本征矩阵不能应用于共面的情形。我们知道一个向量和自己叉乘结果等于0，所以有

x^2x2=0→x^2Hx1=0

另外，任意三维向量 u 和 x2 的叉乘肯定垂直于向量 x2 ，所以有：

u^x2⊥Hx1⇒(u^x2)THx1=0⇒−xT2u^Hx1=0⇒xT2u^Hx1=0

所以我们能得到 E=u^H ，这说明 E 在这种情况下有无穷多解都能满足 xT2Ex1=0 ，这个时候还用8点法，肯定是不行了。

总结

总算写完了，推荐大家去读Yi Ma的书《An Invitation to 3D vision》上面几乎都来自于这本书，同时之前也提到过TUM的Prof.Cremers上课就是用的这本书。除此之外，再推荐个基于该书的课程。视觉几何真心水深，没有理论积累，没有前人指点，坑是填不完的，祝好(对大家，也是对自己)。

（转载请注明作者和出处： http://blog.csdn.net/heyijia0327 未经允许请勿用于商业用途）

【版权声明】泡泡机器人SLAM的所有文章全部由泡泡机器人的成员花费大量心血制作而成的原创内容，希望大家珍惜我们的劳动成果，转载请务必注明出自【泡泡机器人SLAM】微信公众号，否则侵权必究！同时，我们也欢迎各位转载到自己的朋友圈，让更多的人能否进入到SLAM这个领域中，让我们共同为推进中国的SLAM事业而努力！
【注】商业转载请联系刘富强（liufuqiang_robot@hotmail.com）进行授权。普通个人转载，请保留版权声明，并且在文章下方放上“泡泡机器人SLAM”微信公众账号的二维码即可。

ref：已在总结中指出，不再列举。