其实这篇文章讲的就是类似于MATLAB中的mesh函数的实现原理。想要实现的功能就是已知网格三维坐标,如何将转成在某个视角下的二维坐标。说白了就是如何将三维坐标用电脑呈现出来(因为电脑平面是二维的)。比如下面这些三维坐标点。
具体步骤
主要分为三步骤:
1、选定观察点P(默认与x轴37度,与z轴30度,与原点距离(R)足够远)
2、通过空间坐标变换,将原来的空间坐标系转换为以观察点为原点,PO为z轴的空间坐标系。
3、通过投影将三维空间坐标映射到平行于xoy平面的画布上。
步骤一
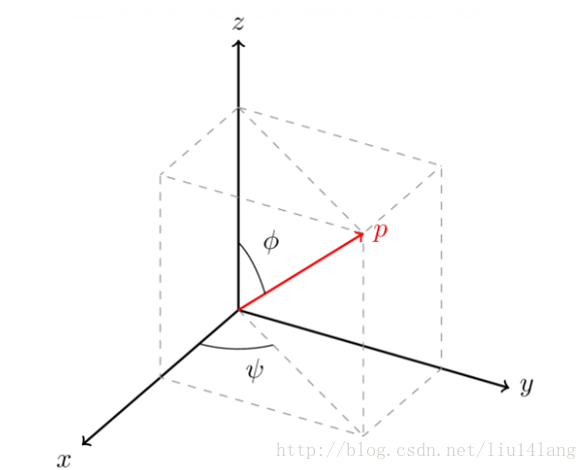
选定观察点,如下图的观察点P
步骤二
通过空间坐标变换,将原来的空间坐标系转换为以观察点为原点,PO为z轴的空间坐标系。
我们所说的空间坐标变换就是换个参考系,比如绕X,Y,Z轴旋转。可以感受一下(此三幅图,盗取的他人的,来源已不详,若给作者造成不便,还望与我联系)
绕X轴:
绕Y轴:
绕Z轴:
以上是直观的显示,那我们如何求得变换后的坐标呢,这不,旋转矩阵派出用场了。
空间坐标变换——旋转矩阵(维基百科)
旋转可分为主动旋转与被动旋转。主动旋转是指将向量逆时针围绕旋转轴所做出的旋转。被动旋转是对坐标轴本身进行的逆时针旋转,它相当于主动旋转的逆操作。
所以要想实现第二步骤,则只需这两步:
步骤三
通过投影将三维空间坐标映射到平行于变换后参考系的xoy平面的画布上。
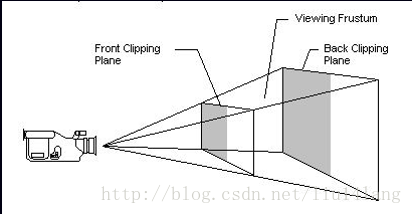
如下两图:
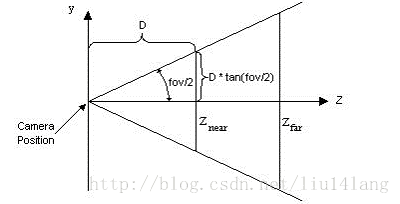
先来解释第一幅图什么意思,第一幅图的意思是那个摄像机的位置就相当于观察点位置,那两平面左边的就是画布,右边代表的是经过任何一个待映射空间点Q且平行于xoy平面的平面。类似于从摄像机位置发出一条直线指向Q,与画布有一个交点R,我们最终要求的就是这个R在画布上的坐标。
第二幅图的意思就是如何求R在画布上的坐标,在这求x为例(求y类似)。途中绿点代表Q,图中的×代表R,我们会给定观察点与画布的距离。
所以R坐标求解如下图所示:
大功告成!!!












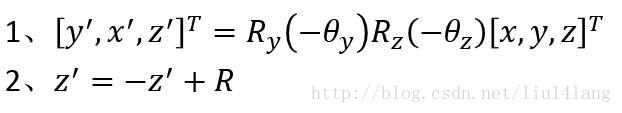

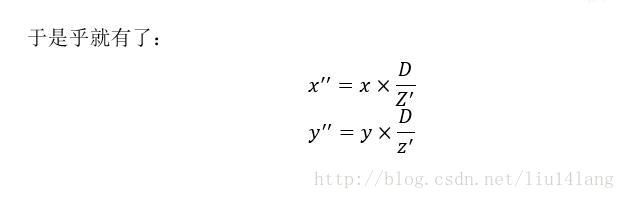
















 3642
3642

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








