【永磁同步电机】基于自适应SDRE的非线性无传感器速度控制PMSM驱动器研究（Simulink仿真实现）

最新推荐文章于 2025-05-07 11:32:59 发布

长安程序猿

最新推荐文章于 2025-05-07 11:32:59 发布

阅读量535

点赞数 15

文章标签：算法

本文链接：https://blog.csdn.net/Yan_she_He/article/details/147742523

版权

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

一、引言

二、研究背景与意义

三、系统动态模型

四、自适应SDRE控制器设计

五、无传感器速度估计器实现

六、控制器与估计器连接

七、仿真与实验验证

八、结论与展望

📚2 运行结果

🎉3 参考文献

🌈4 Simulink仿真、Matlab代码实现

💥1 概述

基于自适应SDRE的非线性无传感器速度控制PMSM驱动器的方法是基于状态相关的Riccati方程（SDRE）控制技术的最新进展。该方法通过梯度型神经网络的实时计算方法，实现了在线控制PMSM的目标。这一创新性的方法不仅克服了传统控制方法中对传感器的依赖，还提高了控制系统的鲁棒性和性能。通过实时计算方法，系统可以更加灵活地应对外部环境变化和负载扰动，从而确保PMSM驱动器的稳定性和可靠性。这一方法的提出将为PMSM驱动器的控制领域带来新的突破，为工业应用和科研领域提供了更加可靠和高效的控制方案。

基于自适应SDRE的非线性无传感器速度控制PMSM驱动器研究是指基于自适应系统动态逆控制（SDRE）的技术，针对永磁同步电机（PMSM）驱动器，研究开发一种无传感器的非线性速度控制方法。

永磁同步电机是一种高性能的电机，通常用于需要高效率和高性能的应用领域，如电动汽车、工业驱动和风力发电等。传统的PMSM速度控制通常需要使用传感器来获取电机的转速信息，但传感器的使用会增加成本和复杂性，因此研究无传感器的速度控制方法对于PMSM驱动器的发展具有重要意义。

自适应系统动态逆控制（SDRE）是一种非线性控制方法，可以适应系统的非线性特性，并且不需要精确的系统模型。基于SDRE的无传感器速度控制方法通过利用电机的非线性特性，结合自适应控制策略，实现对PMSM驱动器的高性能速度控制，同时避免了传感器的使用。

这项研究的目标是开发一种高效、高性能的PMSM速度控制方法，通过实验和仿真验证，证明基于自适应SDRE的非线性无传感器速度控制方法在PMSM驱动器中的可行性和优越性。这样的研究有望为PMSM驱动器的应用提供更加先进和可靠的控制技术。

一、引言

永磁同步电机（PMSM）因其高性能、高效率的特点，在现代工业驱动系统中得到了广泛应用。然而，传统的PMSM速度控制方法通常依赖于传感器来获取电机的转速信息，这不仅增加了系统的复杂性和成本，还可能因传感器故障而导致系统不稳定。因此，研究无传感器的速度控制方法对于PMSM驱动器的发展具有重要意义。本文旨在探讨基于自适应系统动态逆控制（SDRE）的非线性无传感器速度控制方法在PMSM驱动器中的应用。

二、研究背景与意义

PMSM作为一种高性能电机，具有低速性能优良、动态特性好、调速范围宽广等优点，在电动汽车、工业驱动和风力发电等领域得到了广泛应用。然而，传统的速度控制方法依赖于传感器，这限制了其在某些特定场合的应用。无传感器速度控制方法能够克服这一限制，提高系统的可靠性和稳定性。基于自适应SDRE的非线性无传感器速度控制方法，通过利用电机的非线性特性，结合自适应控制策略，实现对PMSM驱动器的高性能速度控制，具有重要的研究价值和应用前景。

三、系统动态模型

为了实现基于自适应SDRE的非线性无传感器速度控制，首先需要建立PMSM的动态模型。该模型通常由磁链方程、电流方程和机械方程等组成，描述了电机的电磁和机械特性。根据电机的具体参数和特性，可以推导出系统的状态空间表达式，为后续控制器的设计提供基础。

四、自适应SDRE控制器设计

自适应SDRE控制是一种基于Riccati方程调节器的非线性控制方法，它通过自适应参数来优化控制器的性能。基于系统的状态空间表达式，采用自适应SDRE控制策略进行设计，具体步骤包括：

设置控制器结构，定义控制误差目标和性能指标。
计算状态反馈增益矩阵和Riccati方程解，以得到控制器的参数。
引入自适应机制，根据系统的实时状态调整控制器参数，以实现更优的控制效果。

五、无传感器速度估计器实现

由于无传感器速度控制需要获取电机的转速信息，因此需要实现无传感器速度估计器。可以采用滑模观测器或其他速度估计器来实现这一功能，以获得无传感器的速度测量。无传感器速度估计器的准确性对于控制系统的性能至关重要。

六、控制器与估计器连接

将自适应SDRE控制器和无传感器速度估计器与电机的动态模型相连接，确保控制器能够接收估计到的速度信号，并提供相应的控制输出。这一步骤是实现无传感器速度控制的关键。

七、仿真与实验验证

在Simulink环境中建立仿真模型，进行仿真验证。通过逐步参数调整和性能评估，对控制系统进行调试和优化。同时，进行实验研究，以验证所提方法在实际应用中的可行性和优越性。

八、结论与展望

本文研究了基于自适应SDRE的非线性无传感器速度控制方法在PMSM驱动器中的应用。通过仿真和实验验证，证明了该方法的有效性和优越性。未来，将进一步研究如何提高无传感器速度估计的准确性和鲁棒性，以及如何将该方法应用于更广泛的工业驱动系统中。

📚2 运行结果

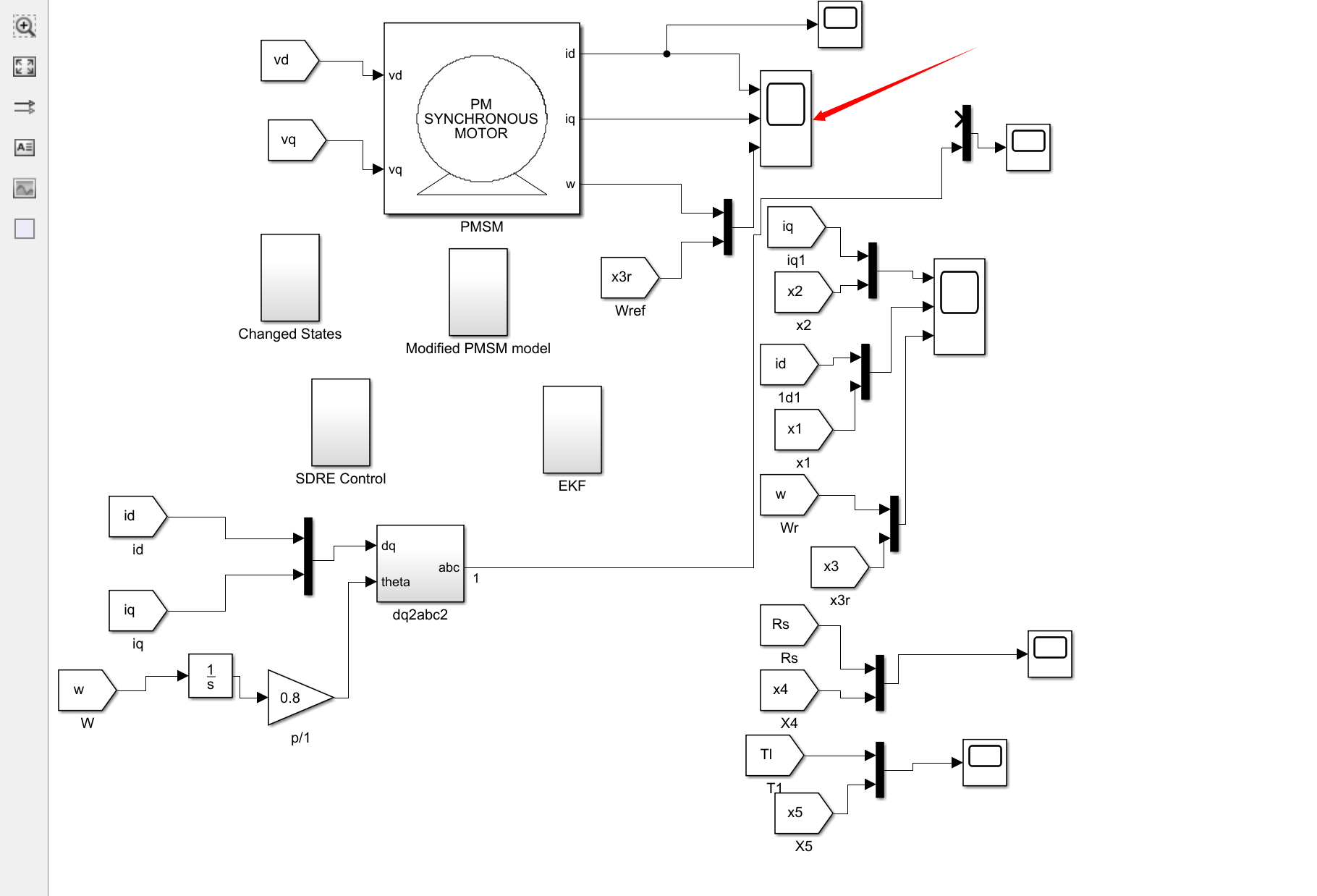
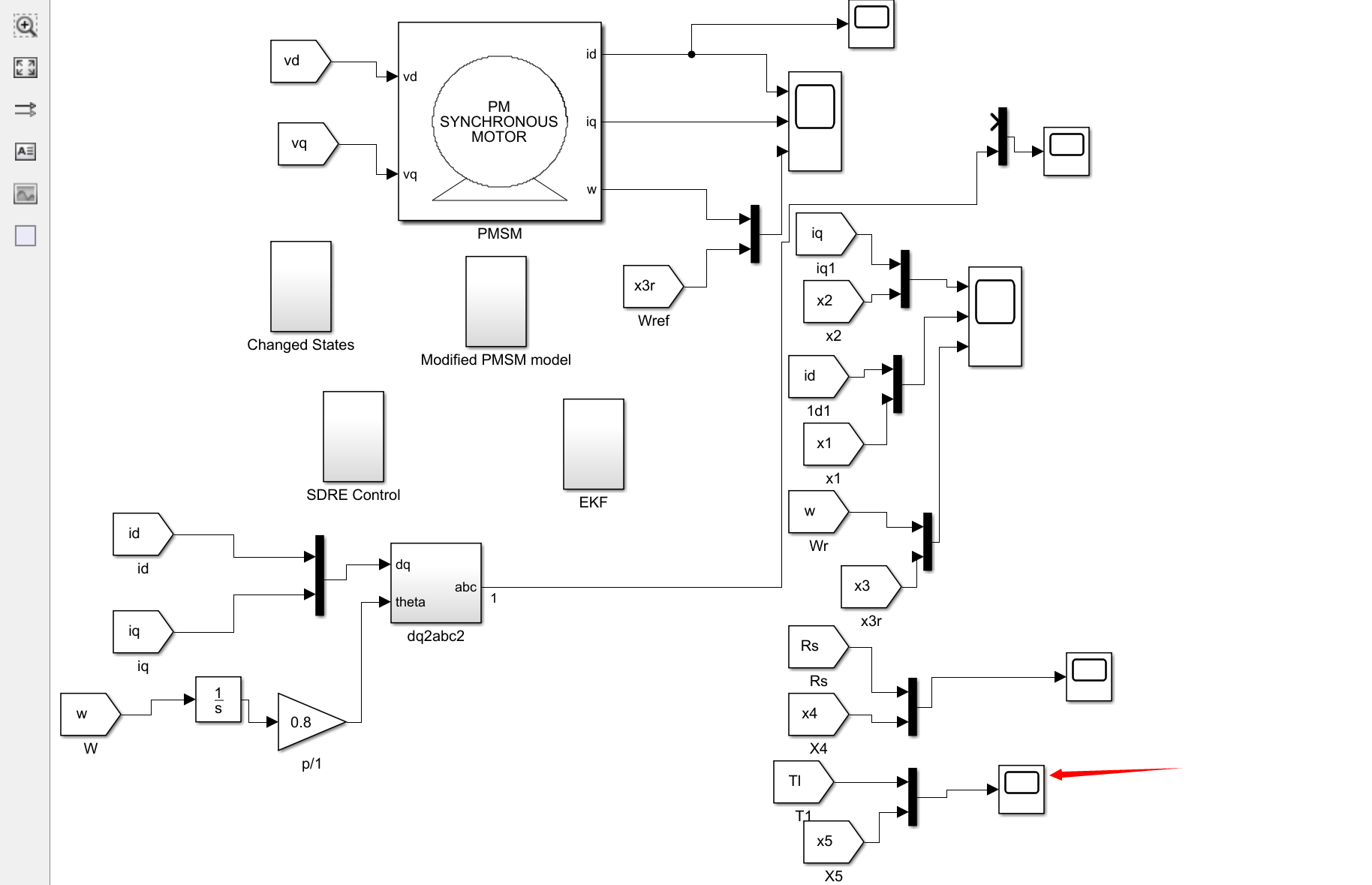
Matlab代码：

clc
clear all

Rs=0.625
Ld=0.036
Lq=0.051
phi=0.545
J=7.5e-4
F=0.036
P=2
% a1=R/Ld
a2=P*Lq/Ld
a3=P*Ld/Lq
% a4=R/Lq
a5=P*phi/Lq
a6=3/2*P*phi/J
a7=F/J
B=[1 0;0 1;0 0]

Qc=[1 0 0;0 1 0;0 0 1]
R=[1 0;0 10]
x2dot=0
x3dot=0
gama=0.1
% syms a1 a2 a3 a4 a5 a6 a7 x1 x2 x3 R
% f=[-a1*R*x1+a2*x2*x3; -a3*x1*x3-a4*R*x2-a5*x3; a6*x2-a7*x3-1/J*Tl;0]
% jacobian(f,[x1 x2 x3 R ])
% E=4300170000*[1e-6 0 0 0 ;0 1e-6 0 0 ;0 0 1e-6 0 ;0 0 0 1e-6 ]
Rk=0.09*[1 0;0 1]
E=4300180000*[1e-6 0 0 0 0 ;0 1e-6 0 0 0 ;0 0 1e-6 0 0 ;0 0 0 1e-2 0; 0 0 0 0 1e-5]