【AlphaFold2】深入浅出，讲解Evoformer|学习笔记

• 博主简介：努力学习的22级计算机科学与技术本科生一枚🌸
• 博主主页： @Yaoyao2024
• 往期回顾：【AlphaFold2】Feature extraction：提取特征，为模型输入做准备|Datapipeline讲解
• 每日一言🌼: 坚持读书，坚持思考，坚持成为你自己🌺

0、前言

本篇博客是围绕youtube德国博主Kilian Mandon(https://www.youtube.com/@KilianMandon/videos)的《从头实现AlphaFold2：AlphaFold Decoded https://www.youtube.com/watch?v=gY4-vVRTkpk》的第五期视频讲解和note-book内容写成的笔记，加上了自己的理解和对相关概念的解释。

再次再次对Kilian Mandon表示感谢！

---

上期我们讲解了AlphaFold2的特征提前的部分【AlphaFold2】Feature extraction：提取特征，为模型输入做准备|Datapipeline讲解。本期，我们将介绍AlphaFold2中最为庞大且最为重要的部分——Evoformer。

一、Evoformer的介绍

就模型参数的数量来说，Evoformer是整个AlphaFold模型中最庞大的部分。整个AlphaFold模型大约有93M参数，其中Evoformer占了88M。Evoformer是类似于Transformer的一种注意力机制框架，从它最后一层网络得出的注意力权重可以看出，它对蛋白质的三维结构已经有了坚实的掌握和理解：

下面的热度图，可视化了注意力权重在训练过程中的变化。底部一行的热度图表明了在哪些氨基酸被用来作为注意力进行更新，它和c图的最终$\text{CA-CA}$（代表每个氨基酸中$\text{C}A$原子之间的距离，是最终模型的预测）距离矩阵的模式非常的相似。

在Evoformer之后的结构模块（ Structure Module）将上述的概念（concept）转换为了真正预测的原子坐标（ actual predicted atom coordinates）。

evoformer由一些相同模块（indentical blocks）组成，其中注意力是它的核心机制（core mechanism)。他比transformer的框架还要复杂一点，但是在这篇博客中我们也会一步一步的去讲解和实现各个部分。

在上期博客讲解特征提取的时候，我们已经看过下图。在feature extraction中，我们已经成功构建了左侧的四个张量。

• extra_msa_feat
• the residue_index
• the target_feat
• the msa_feat

现在我们将先跳过中间的从输入张量到特征编码部分，直接到右侧的Evoformer。

Source: Jumper, J., Evans, R., Pritzel, A. et al. Highly accurate protein structure prediction with AlphaFold. Nature 596, 583–589 (2021).

关于输入编码(input embeddings)我们将在下期进行讲解。因为其中的Extra MSA Stack，相当于是小型的evoformer，所以我们先学习evoformer随后再学习input-embedding这样的方式会相当于比较简单。

如果等不及了，这里先对输入编码进行有一个简单的讲解：

• linear layers：也就是全连接层，进行特征通道维度的变换。
• Outer sum：操作过程和外积(outer product) 很像，只不过把元素乘积的部分换成了元素相加。
• relpos：是AlphaFold对位置编码（positional encodings)的一种处理。
   传统Transformer的位置编码（如正弦函数或可学习向量）直接为每个绝对位置分配一个固定向量，而AlphaFold的relpos创新性地采用残基对的相对位置差作为编码基础。这种设计源于蛋白质结构的核心特性.
• tiling：就是广播（broadcasting)，将其张量广播到更大的形状。（ps: tile本身的疑问含义就是铺地砖，这就和对张量的每个元素看作一个方块地砖进行铺砖，就相当于广播）
• R：可以看到上图右半部分有两个$\text{R}$的操作，它代表的是循环编码（Recycling Embedding），也就是循环执行以上编码操作，用上一轮的输出来更新下一轮的pair和MSA表示（representation）。

---

好，那么现在，我们只需要知道，经过输入特征编码后，我们得到了：

• pair representation ： shape $(\mathrm{r},\mathrm{r},{\mathrm{c}}_z)$
• MSA representation: shape $(s_c,r,c_m)$

($r$代表蛋白质的氨基酸个数， $s_c$是我们选取作为聚类中心的序列数，$c_z$ and $c_m$是编码的特征通道数。

和transformer很像，evoformer也是由一定数量相同的blocks组成，其中每一个Block如下：

它作用于MSA representation 和pair representation，然后将其进行各种变换操作得到具有和输入相同形状的输出。

整个模块如下被分为两个大部分：

• MSA stack
• pair stack

在这两个部分直接有两个information channels，进行信息的交互。

Evoformer的基本idea如下：

我们想对输入实施注意力机制（有关注意力机制的讲解可以看前面几期博客），但是输入展平成序列后对于注意力机制来说太大了（too big to do a full attention mechanism.）。想象一些我们对一个有400个氨基酸长度的蛋白质序列进行操作，那么得到的pair-representation 将会有160,000 项（entries，词目）作为一个序列输入注意力机制。对于注意力机制来说，这是一个长度极长的序列。对比于标准的GPT-4模型（用于8k tokens的上下文窗口），我们的160，000长度的序列输入注意力机制，按照要求，我们得到得分矩阵的大小是序列长度的平方，意味着我们需要102 Gigabytes的显存仅仅用来存储一个注意力模块。

经过上述分析，想完整对整个蛋白质的pair-represengtation来进行注意力机制的运算，几乎是不可能的，其实也没有必要。于是AlphaFold的提出了一种新型的注意力机制： row-wise or column-wise attention（行注意力 & 列注意力）。

如下图所示，对于400个氨基酸，如果进行行注意力，我们将单独的对每一行的序列进行注意力运算，意味着每一行我们仅仅需要 $400^2$ 的注意力得分，总共只需要$400^3$，大概是256 megabytes一个注意力矩阵。

我们可以在以下Evoformer的算法流程图中，看到它是如何使用这种注意力机制的：

1. 在 MSA stack 中，使用行注意力（用pair-representation作为bias)、列注意力、transition（其实就是两层前馈全连接神经网络）、外积（沿着氨基酸的维度作外积然后在序列维度进行平均）来将MSA-representation转为$(s,r,r)$的形状，来和下面 的的pair-representation进行逐元素相加。

整个evoformer的伪代码表示如下（来源于alphafold2的supplement材料）。

2. 在 pair stack 中可能会和之前的注意力模块稍微不太一样。它一共也是有两个注意力模块

• triangle attention around starting node
• triangle attention around ending node （使用pair representation本身作为偏置）。

我们可以注意到，这两个注意力机制的名字都有个 ‘triangle’，其实这来源于一个很cool的解释：

  使用注意力机制中的bias作为第三条边来完成氨基酸之间的三元相互作用建模（这个会在之后具体讲解）。

在这个三角注意力之前还有两个关于三角的更新模块，为： row-wise and column-wise sum-products 。同样也是使用这个’triangle’的Idea。transition module和前面MSA的transition module一样，都是两层前馈(feed forward)神经网络。

不过这些注意力机制也都是基于我们前面实现过了的multihead-attention，只需要指定不同的注意力实施的维度（attn_dim)即可实现行注意力和列注意力，同时在需要的时候指定所用的bias。

---

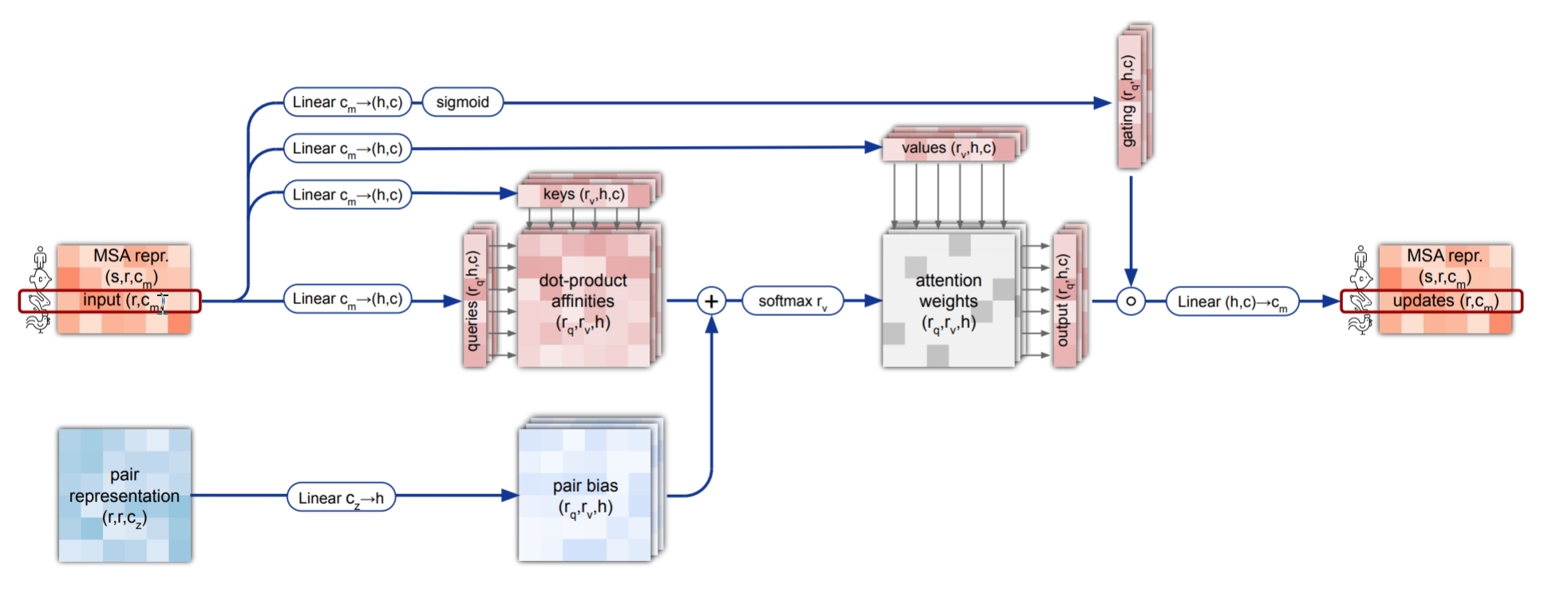
在我们开始之前，我们先简单的回顾一下注意力机制。如下图，对于有偏置的门控自注意力机制（gated self-attention with bias), 我们首先会通过四个线性层对我们的输入序列进行编码得到4个如下的embedding：

1. key
2. query
3. value
4. gate

我们对每个query和每个key进行缩放点积操作（scaled dot-product of each query with each key），得到注意力得分矩阵，并加上bias，再使用softmax进行归一化后得到注意力权重。

然后，对于每个query，我们会按照这个query对应的每个key的权重，区队当前value进行加权求和得到这个query的结果。每个query都是这样计算便得到最终的输出。随后将其和门控编码（gate embeddings)相乘，被$sigmoid$函数归一化到$(0,1)$ 。再传入先行曾，得到最终和输入形状大小一致的输出。

注意，在线性层我们看到它把输入的特征通道从从$c_i$转换到 $(h,c)$，其实是把$c_i$先通过线性层转换为$h\ast c$，随后将其reshape成$(h,c)$

所以可以看到，如果我们想要对MSA representation 或者 Pair representation进行注意力机制的操作，我们首先的第一件事就是： 确定我们的输入序列是什么 (select the input sequence)！

如下图，如果它是 行注意力（ rowwise attention） 机制，注意力的输入就是每一行的对应的序列（one row of the representation）。我们可以看到，在MSA-Stack的行注意力机制中，使用pair-representation作为偏置bias，这样可以工作的很好，因为偏置和注意力权重的矩阵几乎吻合。我们只需要用一个线性层把bias的特征通道的维度进行转换成注意力头数h。

ps：下图中的pair-representation虽然可视化的看上去好像不是都是三阶张量，但是其实只是因为在pair-representation可视化的张量形状上来看，每一个有颜色的小方块都可以看作一个容器，它的每个元素都是$c_z$维的向量；但在bias中，每个方框也同样是一个容器，但是每个元素就是一个具体的数值。所以从张量的结束来看，他们都是三阶张量，都有三个dimesions。

现在我们了解了大致的原理，让我们从MSA-stack到pair-stack输入学习以下每一个模块的实现和作用。

2. msa-stack

2.1 行注意力—row_wise attention

下面是AlphaFOld论文中有关行的门控自注意力机制以pair-representation作为bias的伪代码，可以在其补充材料中找到。

符号规定：

• $\mathbf{m}$：张量，也就是上图中的注意力左侧的输入：MSA representation。形状为(*, N_seq, N_res, c_m)

• ${\mathbf{m}}_{si}$：向量，代表每个特征编码后的氨基酸的向量。可以理解为第$s$条序列的第$i$个氨基酸，用$c_m$维向量进行了编码；$s$也就是行坐标（row-index)、$j$是列坐标（column-index)。

• { m s i } \{\mathbf{m}_{si}\} {msi​}：集合，可以认为是包含了每个氨基酸的集合，每个元素是一个特征向量。

• $\mathbf{z}$：张量，pair-representation。形状为shape (*, N_res, N_res, c_z)

• ${\mathbf{z}}_{ij}$:向量，第$i$行第$j$列的pair特征编码。

• { z i j } \{\mathbf{z}_{ij}\} {zij​}：同上，含义类比。

• ${\mathbf{q}}_{si}^h,{\mathbf{k}}_{si}^h,{\mathbf{v}}_{si}^h$：向量，每个氨基酸被重新编码，改变特征维度为$c$.($h$代表是第$h$个注意力头。

• $b_{ij}^h$：单个数字，代表第h个注意力头对应的注意力权重矩阵$(i,j)$位置的分数所需要加上的偏置。

讲解：

代码首先进行了一个对每个氨基酸特征维度编码的归一化（normalization)。第2行和第4行，通过输入线性层为注意力机制构建query,key,value,gate embeddings。

在第3行，pair-representation的特征维度$c_z$被无偏置的线性层重新编码为$h$，再进行归一化，为每一个注意力头提供偏置bias。

Note：加粗的字符代表的是向量（vector)，没有加粗的代表是数字，比如$b$。

列坐标决定了注意力机制的发生（The column index on the other side is where the attention mechanism happens）。

在第5行和第六行，我们可以看到数学表达式的行注意力机制。之所以是行注意力机制是因为在q,k,v进行计算的过程中，一直带着行坐标$s$( row index, s)，以及在进行门控操作时。但其实，真正的注意力发生的维度（真正进行信息交互的维度）即attn_dim，是列维度。其中在query中，$i$表示列维度（第s行第i列）；在key中，$j$表示列维度（第s行，第j列）。可以看到行始终还是一行，是同一行中的元素（不同列）之间在点积的过程进行信息的交互。同时，注意力维度决定了softmax进行归一化的时候沿着哪个维度。

所谓注意力维度attn_dim其实在上上篇讲注意力机制的实现那篇博客讲过了。这里再次回顾一下，所谓的attn_dim就是在哪个维度上对应了具体不同的一个个key或者query，这个维度的每个元素之间进行交互，计算之间的相似度，得到注意力得分。显然，在上述讲述的行注意力当中，行坐标s只是觉得了选取哪个作为输入序列，真正注意力发生的维度还是列坐标，同一行不同列之间的元素进行信息的交互，不同行之间没有信息交互。

在第7行，注意力头的输出被拼接在一起，然后送到输出的线性层，将氨基酸的特征维度重新编码回 $c_m$。

这个伪代码表示的过程和上面行注意力机制的流程图是一致的，即使符号表示上有些奇怪。

因为我们已经实现了多头注意力机制，这里我们只需将其当成现成的，准备好输入张量输入到注意力模块即可得到输出。如下图右侧的实现代码差不多

讲解：

第一行相当于左侧伪代码的第1，3行。$\text{b.moveaxis}(-1,-3)$ 移动坐标交换维度，是因为在我们实现的注意力模块中，注意力头的数量需要在倒数第三个维度，即-3，所以将其最后一个维度和倒数第三个维度进行了交换（(*, z, z, N_head) -> (*, N_head, z, z))。

在真正的行注意力算法的实现过程中，我们所需要做的是把msa矩阵$\mathbf{m}$还有pair得到的bias矩阵$\mathbf{b}$都输入到多头注意力mha模块当中，指定注意力发生的维度即可）。

Note： 对于row-wise行注意力，我们需要指定column dimension列维度最为注意力维度（ for row-wise attention, we’d need to specify the column dimension as the attention dimension, ），因为在行注意力执行的过程中，列索引是真正被cycle through遍历，以及是后面进行与value矩阵的相乘后求和的维度。

---

2.2 列注意力—colum-wise

列注意力和行注意力流程基本一致，不一样的地方如下

• 没有偏置bias
• 注意力维度发生在列维度。

从下图中可以看到，列索引 $i$ 在注意力机制执行的过程中一直被保留，keys和queries的 每一个元素向量的相乘 （each-with-each vector multiplication） 是沿着行维度进行的( happens along the row-dimension)，分布用$t,s$表示。即：$t,s$是注意力发生的维度，即 attn_dim！

Note：上图的伪代码由视频博主给出，和AlphaFold2中论文补充材料里给定的伪代码在第五行并不一致，这里我也认为博主的写法是正确的。

2.3 msa-transition：

MSA Transition是Evoformer中MSA堆栈的最终处理层，其实就是两层前馈神经网络（在输入前进行了normalization归一化）。其核心作用是通过非线性特征变换增强MSA表示的表达能力。它采用标准的 前馈神经网络(FFN) 架构，主要实现。

它首先对输入的张量的特征通道数×4，得到一个更高维的特征表示，然后再将其变化回原来的形状。

类比总结：

步骤	榨汁机类比	AlphaFold实际操作	作用
扩展维度	把苹果切块详细检查	64维 → 256维	拆解特征细节
ReLU	扔掉发苦的果块	负数归零，正数保留	过滤噪声
压缩维度	榨成一杯混合果汁	256维 → 64维	综合关键信息

• Pre-LN的优势：先归一化再变换，提升训练稳定性（尤其对深度网络）
• 4倍扩展的合理性：
  • 足够空间编码氨基酸替代矩阵（20×20的组合效应）
  • 与注意力头维度（通常32）形成互补表征
• 无残差连接：因Evoformer外层已有残差连接，避免冗余

下面这样一个前馈神经网络是transformer典型的一个模块。其中 n =4 作为放缩因子——scaling factor.

2.4 外积+平均——Outer Product Mean

到这里，我们已经讲完了MSA-stack的前三个模块,其输出通过Outer Product Mean与 pair-stack相连。

Outer Product Mean的作用就是将MSA-representation的形状reshape到pair-representation相同的形状。

之前在张量的操作那篇博客里面也讲到，一般外积操作就是用来调整张量的形状的。

$⨂$：for the outer product（外积）

讲解：

1. 从代码可以看到，外积并不是$\mathbf{m}$和$\mathbf{m}$自己做内积，而是来自于通过来自于$\mathbf{m}$的线性编码的行序列$\mathbf{a}$和$\mathbf{b}$做外积。这样可以增加模型的灵活性（解耦特征：避免原始特征的强耦合。）来给外积的结果带来意义（模型可以学习不同的相互作用模式。）。

2. AlphaFold 的 Outer Product Mean 操作实际上包含两个层次的外积计算：

   • 位置维度外积（i 与 j 的交互）：决定哪些残基对需要计算相互作用

   • 通道维度外积（c 与 c 的交互）：决定这些残基如何相互作用

     这就像相亲配对时：

   • 第一重外积：确定谁和谁见面（i-j 配对）

   • 第二重外积：记录他们聊了什么话题（化学键/疏水作用等)；具体来说，就是特征维度不同通道之间的元素相乘（c outer-product c -> c x c)。

   为什么需要这个？
   原始通道可能代表：

   • a 的通道：电荷、极性
   • b 的通道：疏水性、体积

   外积后得到 所有特征的组合（如电荷×疏水性），捕捉更复杂的相互作用。

3. 通过这样的外积操作后（${\mathbf{a}}_{si}\otimes {\mathbf{b}}_{sj}$），得到的张量的形状为(*,N_seq, N_res, N_res, c, c)。然后再沿着序列也就是行的维度进行压缩求平均：${\text{mean}}_s({\mathbf{a}}_{si}\otimes {\mathbf{b}}_{sj})$ 得到的张量的形状为(*,N_res, N_res, c, c)。然后对最后两个特征维度flatten，得到张量的形状为：(*,N_res, N_res, c*c)

4. 第四行对再次经过线性层，reshape特征维度（c*c -> c_z)。最终得到的张量形状为(*,N_res, N_res, c_z)，和pair_representation的形状一致。

python的实现代码如下图右侧所示（一个爱因斯坦操作即可代表二重外积+求和操作，在最后除以N_seq进行平均）。

在上述python的实现代码中的einsum表达式，我们沿着序列维度，也就是行的维度N_seq进行了收缩（求和），之后在线性输出层输出后进行除以N_seq求平均。这和论文中的伪代码的操作流程稍有不同。这对模型的预测没有很大的影响。但是如果想训练模型的话，最好还是按照伪代码的流程进行代码的实现让模型得到更好的效果。

---

3. pair-stack

MSA-stack执行完后，接下来到了pair-stack。在之前的Evoformer的架构图和伪代码中，我们注意到，大部分模块都是以三角（triangle)开头命名的。在正式讲解具体算法之前，我们来聊聊这个triangle。

深入解析 Pair Stack 中的三角机制与信息流动：

在理解三角机制之前，我们来思考一下特征表示应该怎么真正的进行编码。对于上面讲到的MSA-representation，它的编码含义就很容易理解。

3.1 MSA和pair编码的含义

1. MSA表示的本质

MSA（多序列比对）矩阵可以看作一个进化信息库：

• 行（Row）方向：不同同源物种的序列（如人类、小鼠、果蝇的同一蛋白质）
• 列（Column）方向：蛋白质的残基位置（如第10位氨基酸在所有物种中的变异情况）

序列/残基	位置1	位置2	…	位置N
物种A	Val	Leu	…	Asp
物种B	Ile	Leu	…	Glu
…	…	…	…	…
物种S	Ala	Phe	…	Asp

2. 行操作 vs 列操作的生物学意义

操作类型	计算维度	生物信息流	结构预测作用
行操作	同物种内跨位置	单个蛋白质内部的残基间协同进化	捕捉局部结构（如α螺旋的周期性）
列操作	同位置跨物种	不同物种间同一残基的保守性/变异模式	识别关键功能位点（如活性中心）

但是，到了氨基酸对表示pair-representation，它的编码意义就没有那么的明晰了。根据它的名字，我们希望是每一项能够能够表示一对氨基酸之间的关系信息（ information on the interaction between pairs of residues）。事实上，对于每一对氨基酸，对应一个矩阵里的两项：(i, j) 和 (j, i)。把两个氨基酸i,j看作一个节点，(i, j) 和 (j, i)就像两条有向边：

1. ij代表从i到j的信息
2. ji代表从j到i的信息

1. Pair Representation 的本质
Pair Stack 的核心是残基对表示矩阵 Z ∈ ℝ^(N×N×c_z)，其中每个 Z[i,j] 和 Z[j,i] 是两个独立的向量。这种设计隐含了方向性信息传递的假设：

条目	理论解释	类比	生物学意义
Z[i,j]	残基i→残基j的信息流	“i 对 j 说的话”	i的化学性质如何影响j的空间位置
Z[j,i]	残基j→残基i的信息流	“j 对 i 的回复”	j的结构约束如何反馈给i

示例场景：

• 谷氨酸（i，带负电）→ 甘氨酸（j，中性）：
  Z[i,j] 可能编码静电排斥作用
  Z[j,i] 可能编码甘氨酸的构象灵活性带来的容忍度

2. 为什么需要双向条目？

场景	单向表示的问题	双向表示的优势
静电相互作用	无法区分 donor/acceptor	Z[i,j]和Z[j,i]可分别编码
氢键网络	只能描述单方向供体-受体	完整描述双向氢键可能性
空间位阻	无法区分i-j和j-i的碰撞	独立建模两个方向的立体约束

3. 学习到的特征（Learned Features）
尽管缺乏明确的物理解释，实践中这些向量会自组织地编码：

• 局部相互作用（3-5Å）：
  • Z[i,j]：i的侧链如何影响j的主链构象
  • Z[j,i]：j的二级结构倾向如何限制i的旋转
• 全局协调（>10Å）：
  • 通过多轮信息传递实现长程协调

4. 成功的关键因素

1. 冗余设计：
   双向条目提供信息冗余，增强模型容错能力（即使一个方向信号噪声较大）
2. 几何完整性：
   三角机制确保 Z[i,j] 和 Z[j,i] 最终收敛到物理合理的对称状态（如距离矩阵必须对称）
3. 层次化学习：
   • 浅层网络：学习局部物理化学规则（如范德华半径）
   • 深层网络：整合长程协调（如结构域间相互作用）

5. 与MSA Stack的协同作用

---

3.2 介绍：用三角注意力更新

有上面对pair-representation的编码表示，我们知道每一项表示的是两个氨基酸之间的直接交互信息，现在让我看一下基于这个pair矩阵，注意力机制是如何执行的。

如下图，假如说我们想通过ik来更新ij项（update the pair ij from the pair ik.）：

将i代表的氨基酸节点看作起始节点，用ik边去更新ij，这被称为：

外展更新（Outgoing Update / 起始节点更新 update around the starting node）：

操作逻辑

• 目标：用所有以残基i为起点的边（z_ik）来更新目标边z_ij
• 关键点：引入第三边z_jk作为偏置（bias），形成完整三角形

数学实现

1. 注意力权重计算：
   $${\alpha }_{ijk}=\text{softmax}\left(\frac{Q(z_{ij})\cdot K(z_{ik})}{\sqrt{d}}+b(z_{jk})\right)$$

   • Q(z_ij)和K(z_ik)：查询-键交互，衡量i-j与i-k的相关性
   • b(z_jk)：偏置项，编码j-k的物理约束

2. 加权聚合：
   $$z_{ij}^{\text{new}}=\sum _k{\alpha }_{ijk}\cdot V(z_{ik})$$

生物学意义

• 空间合理性：防止更新后的z_ij与z_ik、z_jk产生几何冲突
  • 例：若z_ik=5Å且z_jk=3Å，则z_ij必须满足2Å ≤ z_ij ≤ 8Å
• 方向性建模：i→j的信息流受i的其他连接（i→k）影响

内收更新（Incoming Update / 终止节点更新）:

操作逻辑

• 目标：用所有以残基j为终点的边（z_kj）来更新目标边z_ij
• 关键点：引入转置边z_ki作为偏置

与Outgoing Update的对比

特性	Outgoing Update	Incoming Update
固定索引	起始节点i（行操作）	终止节点j（列操作）
依赖边	z_ik（同源边） + z_jk	z_kj（同源边） + z_ki
生物意义	调控i的局部环境	调控j的局部环境

为什么需要两种更新？

• 结构完整性：
  • Outgoing更新确保残基i的连接自洽
  • Incoming更新确保残基j的连接合理
• 信息互补：
  • 例：活性位点残基i需要同时考虑：
    • 它如何影响周围残基（Outgoing）
    • 周围残基如何约束它（Incoming）

💡有了以上关于三角机制的概念，我们再来看到整个pair-stack的架构：
第一个和第三个block使用了外展边/起始节点注意力，可以被认为是一种行的操作（可以把i看作行的索引）—— row-wise operations,
其他两个利用三角机制更新的block使用了incoming edges和终止节点注意力，是列操作——column-wise operations.

3.3 三角乘积更新

在论文中具体的三角形乘积更新也分为外展更新和内收更新的图示和伪代码如下：

符号规定：

• $\odot$：逐元素乘法

讲解：

乘法更新，首先从pair-representation构建两个a,b编码：${\mathbf{a}}_{ij},{\mathbf{b}}_{ij}=\mathrm{sigmoid}\left(\mathrm{Linear}({\mathbf{z}}_{ij})\right)\odot \mathrm{Linear}({\mathbf{z}}_{ij}){\mathrm{a}}_{ij},{\mathbf{b}}_{ij}\in {\mathbb{R}}^c$。 然后使用${\mathbf{g}}_{ij}=\text{sigmoid}\left(\mathrm{Linear}({\mathbf{z}}_{ij})\right)$构建门控编码。

真正有意思的是第四行的代码，也是真正的在不同位置（不同氨基酸）之间的信息交流（ actual cross-talk between the positions）。使用外展边，ik,jk，其中k是列索引，i,j是固定的行索引也是起始节点。我们的目的是更新边i-j时，考虑所有通过i连接的i-k边和对应的j-k边。

在后面讲到的三角注意力机制，我们也需要把j-k边考虑在内。在这里，我们的实现方式是：估计i和j（行操作），便利k，其中每个a_ik和⭐a_jk向量进行哈达玛积，也就是逐个元素相乘得到新的向量a_ijk，然后将其沿着维度k进行求和，再送入归一化层，然后通过一个线性层之后和门控编码相乘。

对于内收边，我们的操作几乎相同。主要不同的点在下图中用黄色高亮标出。这里，我们同样是对pair-representation中的元素ij进行更新，但是我们是从内收边的角度进行更新，即固定j遍历k，得到所有的kj（内收边）来进行更新ij。同时，为了完成三角关系的建模，我们还需要考虑ki，具体的操作同样还是逐元素相乘，操作对象是ki和kj两列，然后沿着行的维度进行求和。

综上，使用外展边，相当于行操作，我们对a_ik和b_jk进行操作；使用内收边，我们对两列进行操作：a_ki和b_kj。

3.4 三角注意力更新

在进行完三角乘法更新后，会来到两个三角注意力模块，同样分别使用外展边、内守边的概念。

看如下伪代码，是起始节点的三角门控注意力机制，其实就是行注意力机制，只不过使用pair-representation作为了偏置。在第三行，我们可以看到和之前一样，我们也是同样使用线性层来改变输入的张量矩阵的特征通道数为注意力头数，来构建多头注意力机制的偏置。

这种偏置的构建和使用，完全符合我们想要的三角关系：

在更新ij项的时候，ij项本身作为一个query，它可以被所有的k_ik（固定i遍历k，代表的是以i为起始节点的外展边)进行更新。但是同时，我们的注意力得分也受到偏置b_jk的影响，也就是三角形中的第三条边。

终止节点的三角注意力计算过程是基本相同的，不同的点也在下图中用黄色高亮标出。类似的，使用终止节点和之前所讲的列注意力很像，只不过是使用pair-representation自己作为了偏置。

在第五行的索引可以看到：
对于q和k,列索引j是固定的，遍历的是行，索引它是列注意力。使用 query的索引，i作为第一个维度，key的索引k作为第二个维度（是注意力真正发生的维度，也就是行维度），得到的注意力得分矩阵的得分索引为ik。

我们使用ki来索引偏置矩阵得到b_ki（而不是b_ik)，意味着我们在使用pytorch进行实现的过程中，先要对b矩阵进行转置，然后再将其与注意力矩阵相加。

3.5 pair transition

pair-representation的最后一部分也是两个前馈网络，和MSA的前馈网络基本一致。

3.6 整合

综上，我们将以上模块整合到一起，构建整个Evoformer。也就是下面黄色高亮的模块。

可以看到，这些方法按照流程图中的关系和顺序，被有序的调用：首先是MSA-stack——MSARowAttentionWithPairBias, MSAColumnAttention, MSATransition, OuterProductMean；然后是Pair-stack：outgoing triangle multiplication, incoming triangle multiplication, attention around starting node, attention around ending node, and the pair transition.

除了调用这些方法外，我们还可以看到具体实现的一些细节：之前我们也说过，Evoformer是由许多相等的blocks（一共48个）构成，每一个都有自己的权重;上图中的rowwise 和 columnwise dropout可以忽略。 Dropout其实就是一种正则化，

其核心思想是：

• 训练阶段：随机将部分神经元输出置零（概率为p），保留的神经元按1/(1-p)缩放
• 推理阶段：保持原始输出不变（等效于关闭Dropout）
• 目的：防止过拟合，增强模型泛化能力

由于我们并不是训练，只是使用现有的权重进行推理，所以Dropout对我们来说暂时不重要。

另外一个比较重要的细节是，我们并没有直接将每个block的输出作为结果，而是把它和输入加起来。这种操作也被称为残差连接 residual connections 。这种残差连接的方法，能够让训练更加稳定。

如果我们想到类似于三角乘积的这种更新方法，将两行进行相乘，然后相加来得到一个全新的张量，其实这是一个非常transformative 的操作，对原有输大改变很大。在残差连接的情况下，输出只作为一小部分残差和原始输入相加，这意味着模型可以学习到较小的权重，使得嵌入向量的变化不大。残差连接允许输出更像是输入的微小调整（offset)，而不是完全替代。

最终，模型选取MSA representation 的第一行，并且将其输送到线性层，得到的结果称为 single representation，但是其实它只是MSA -representation通过MSA-stack后的一部分。剩下的部分被dropped 并且不会再被接下来的模型使用。事实上，当我们回想我们最初是怎么构建MSA-feature的，它的第一行的真实含义其实就是真正的目标序列（target sequence)，我们也就是要根据这个来预测蛋白质的三维结构。

4. 回顾整个架构

1. 总体结构
Evoformer 由多个相同的 Evoformer Block 堆叠而成，每个 Block 包含：

• MSA Stack（多序列比对栈）
• Pair Stack（配对栈）
• 两个信息通道（MSA ↔ Pair 信息交互）

2. MSA Stack
输入：MSA（Multiple Sequence Alignment）表示（形状：[序列数, 残基数, 隐藏层维度]）
组成模块：

1. Row-wise Attention（行注意力）
   • 对 MSA 的 每一行（序列） 进行自注意力计算。
   • 使用 Pair 表示作为偏置（bias）（类似 Transformer 的位置编码，但动态调整）。
2. Column-wise Attention（列注意力）
   • 对 MSA 的 每一列（残基位置） 进行自注意力计算。
   • 不同序列的相同位置进行交互（类似蛋白质家族中保守残基的建模）。
3. Transition Module（过渡模块）
   • 一个简单的 2 层前馈神经网络（MLP），用于非线性变换。

3. MSA → Pair 信息流动
MSA 表示通过 Outer Product Mean（外积平均） 转换为 Pair 表示：

• 操作：
  1. 对 MSA 的 残基维度（即每个位置的特征） 计算外积（[序列数, 残基A, 隐藏层] × [序列数, 残基B, 隐藏层]）。
  2. 沿 序列维度（sequence dimension） 取平均，得到 [残基A, 残基B, 隐藏层] 的 Pair 表示。
• 作用：
  • 捕捉 残基对（pair） 之间的协同进化信号（如共突变）。
  • 计算后，该结果会 加（add） 到 Pair Stack 的表示中，实现信息流动。

4. Pair Stack
输入：Pair 表示（形状：[残基数, 残基数, 隐藏层]）
组成模块：

1. Multiplicative Updates（乘法更新）
   • 计算方式：
     • 选择 Pair 表示的 两行（或两列），进行逐元素相乘并求和（类似点积）。
     • 例如：output = sum(row_i * row_j)，类似于残基对的相互作用建模。
   • 作用：
     • 增强 Pair 表示中的局部依赖关系。
2. Attention Updates（注意力更新）
   • Row-wise Attention（行注意力）：
     • 对 Pair 表示的 每一行 进行自注意力计算，使用 Pair 表示本身作为偏置。
   • Column-wise Attention（列注意力）：
     • 对 Pair 表示的 每一列 进行自注意力计算，使用 Pair 表示的转置作为偏置。
   • 作用：
     • 建模 长程残基相互作用（如蛋白质三维结构中的远距离接触）。
3. Transition Module（过渡模块）
   • 另一个 2 层 MLP，用于进一步调整 Pair 表示。

5. 关键设计思想

1. 分而治之（Row-wise + Column-wise Attention）
   • 直接对整个 MSA（[序列数 × 残基数]）做全局注意力计算量太大，因此拆分为 行注意力 + 列注意力，降低复杂度。
2. Triangle Attention（三角注意力）
   • Pair Stack 的注意力机制 使用 Pair 表示自身作为偏置，形成类似“三角更新”的机制：
     • 行注意力：Pair[i,j] 受 Pair[i,:] 影响。
     • 列注意力：Pair[i,j] 受 Pair[:,j] 影响。
   • 这种设计能隐式建模 残基对的对称性和传递性（如 Pair[i,j] 和 Pair[j,k] 影响 Pair[i,k]）。
3. 信息流动（MSA ↔ Pair）
   • MSA 提供 序列家族进化信息，Pair 提供 结构约束信息，二者通过 Outer Product Mean 和 残差连接 交互，实现协同优化。

6. 对比 Transformer

特性	Transformer	Evoformer
输入	1D 序列（如句子）	2D 矩阵（MSA + Pair）
注意力机制	全局自注意力	行注意力 + 列注意力 + 三角注意力
偏置	固定位置编码	动态 Pair 表示作为偏置
核心目标	建模序列内部关系	建模序列进化 + 结构约束（3D 接触）
计算效率	适合中等长度序列	通过分解注意力降低大矩阵计算复杂度

7. 总结

• Evoformer 的核心创新：
  • 分解注意力（Row/Column-wise） 处理大矩阵。
  • 三角注意力机制 建模残基对的对称依赖。
  • MSA ↔ Pair 双向信息流动 结合进化与结构信号。
• 虽然比 Transformer 复杂，但每个模块（注意力、外积平均、MLP）本身是简单的，组合后能高效建模蛋白质序列-结构关系。