向量的概念:
向量:
简单理解:具有大小和方向的量称为向量
单位向量:
单位向量是指模等于1的向量。由于是非零向量,单位向量具有确定的方向。
一个非零向量除以它的模(向量长度),可得单位向量:e= AB→|AB|
零向量:
长度(模)等于0的向量叫零向量,零向量方向不确定。
向量的基本运算
向量加法:
向量加法满足三角形法则和平行四边形法则:
假设,a=( x1 , y1 ),b=( x2 , y2 );则:a+b=( x1 + x2 , y1 + y2 )
交换律: a+b=b+a;
结合律: (a+b)+c=a+(b+c);
向量减法:
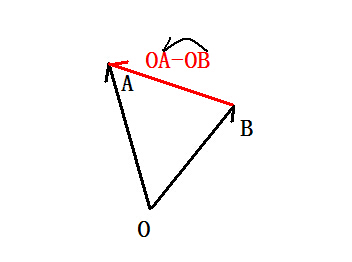
如图所示,两个向量有共同的起点(O),则两个向量的差是以减向量的终点(B)为始点,被减向量的终点(A)为终点的向量(BA)。或简记为“终点向量减始点向量”
通过上图还可以推断出:“从一个向量减去另一个向量等于加上这个向量的相反向量”
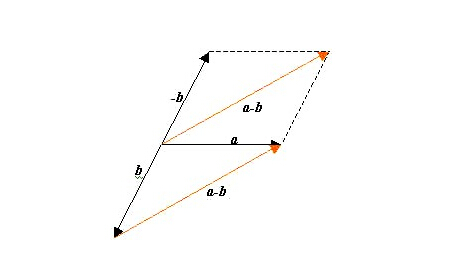
假设,a=( x1 , y1 ),b=( x2 , y2 );则:a-b=( x1 - x2 , y1 - y2 )
交换律: a+(-b)=a-b
向量的数乘:
设λ是一个数量,向量 a⃗ 与λ的乘积规定如下:
1、当λ>0时:向量λ








 本文详细介绍了向量的基础知识,包括向量的概念、单位向量和零向量的定义,以及向量的加法、减法、数乘、正射影和内积的运算。此外,还讨论了向量在坐标系中的表示,如数量积的坐标表达式、向量的长度和距离公式以及夹角公式。这些内容对于理解和应用向量至关重要。
本文详细介绍了向量的基础知识,包括向量的概念、单位向量和零向量的定义,以及向量的加法、减法、数乘、正射影和内积的运算。此外,还讨论了向量在坐标系中的表示,如数量积的坐标表达式、向量的长度和距离公式以及夹角公式。这些内容对于理解和应用向量至关重要。
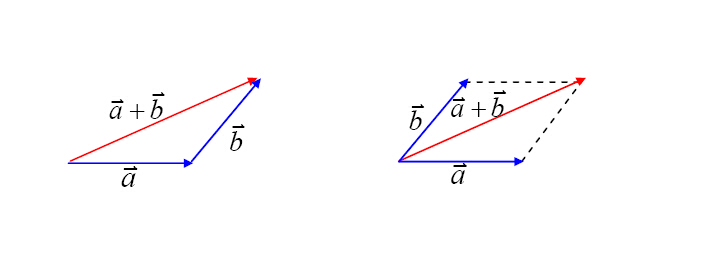
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 873
873

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








