射线与球相交的判断

如下图：

设射线原点是A，射线方向的单位向量是B。

点P在射线上的表示形式是：

               

再设球的原点是C，半径是R，如果点P在球面上，则有：

把 P(t)=A+tB代入上式得：

因为A和C是固定的两点，把A-C=D，即得

然后解方程如下图：

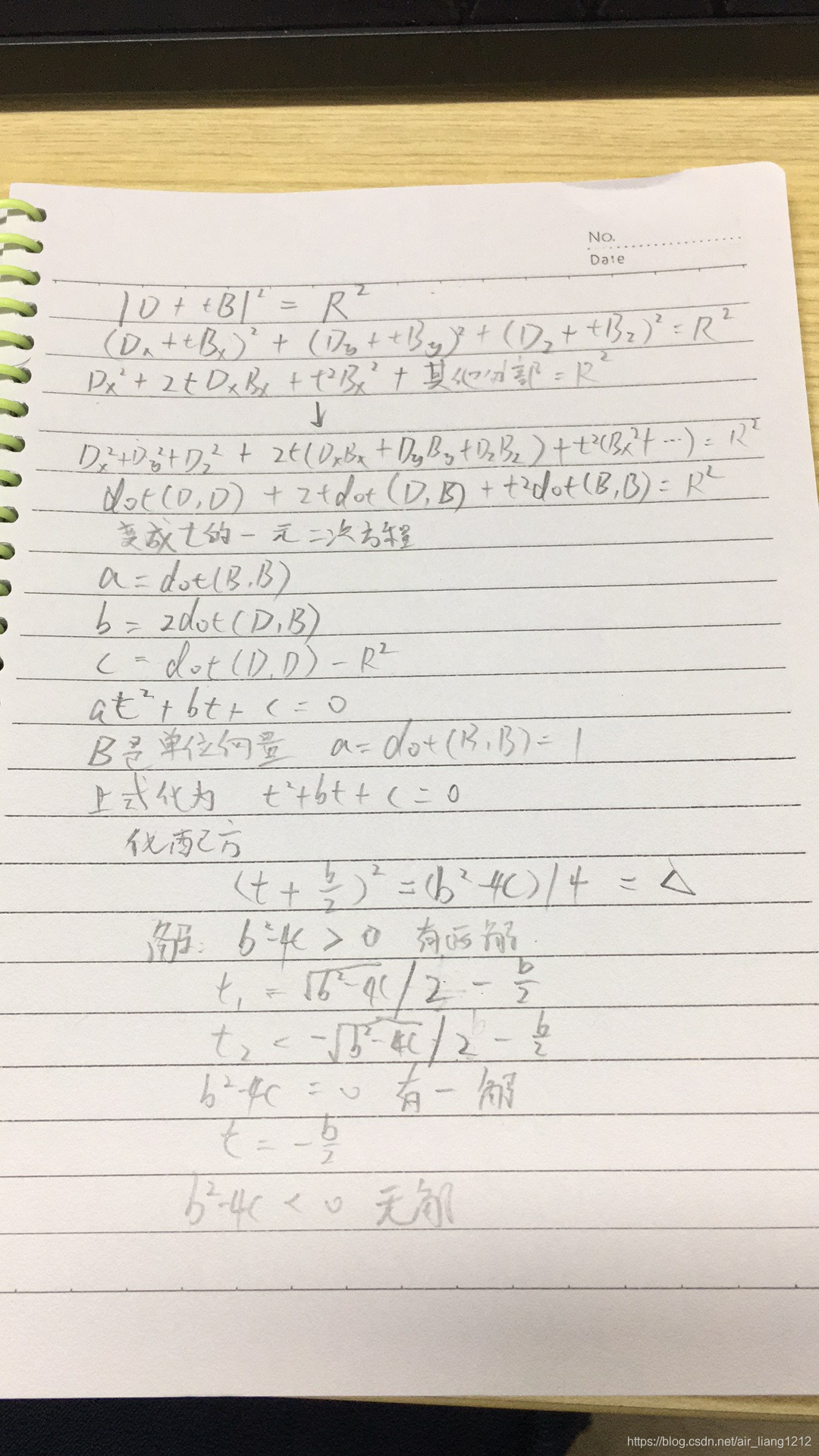
我定定义t0是近点，t1是远点，返回t0代入P(t)就是我们要求的点，代码如下：

bool Hit(const Ray& ray, float& t0, float& t1) const
{
	glm::vec3 oc = ray.mOrig - m_position;
	float a = glm::dot(ray.mDirection, ray.mDirection);
	//一般a是1
	float b = 2.0f * glm::dot(oc, ray.mDirection);
	float c = glm::dot(oc, oc) - mRadius * mRadius;
	float discriminant = b * b - 4 * a * c;

	if (discriminant < 0)
	{
		return false;
	}
	else
	{
		float discriminantK = sqrt(discriminant);
		t0 =  (-b - discriminantK) / (2.0f * a);
		t1 = (-b + discriminantK) / (2.0f * a);

		if (t0 < 0)
		{
			t0 = t1;
		}
	}

	return true;
}