在泛函分析中,卷积(捲積)、旋積或摺積,是通过两个函数f 和g 生成第三个函数的一种数学算子,表征函数f 与经过翻转和平移的g 的重叠部分的累积。如果将参加卷积的一个函数看作区间的指示函数,卷积还可以被看作是“滑动平均”的推广。
目录[隐藏] |
[编辑]简单介绍
卷积是分析数学中一种重要的运算。设: 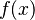 ,
,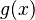 是
是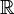 上的两个可积函数,作积分:
上的两个可积函数,作积分:
可以证明,关于几乎所有的  ,上述积分是存在的。这样,随着
,上述积分是存在的。这样,随着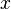 的不同取值,这个积分就定义了一个新函数
的不同取值,这个积分就定义了一个新函数 ,称为函数
,称为函数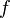 与
与 的卷积,记为
的卷积,记为 。容易验证,
。容易验证, ,并且
,并且 仍为可积函数。这就是说,把卷积代替乘法,
仍为可积函数。这就是说,把卷积代替乘法, 空间是一个代数,甚至是巴拿赫代数。
空间是一个代数,甚至是巴拿赫代数。
卷积与傅里叶变换有着密切的关系。利用一点性质,即两函数的傅里叶变换的乘积等于它们卷积后的傅里叶变换,能使傅里叶分析中许多问题的处理得到简化。
由卷积得到的函数  一般要比
一般要比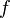 和
和 都光滑。特别当
都光滑。特别当 为具有紧支集的光滑函数,
为具有紧支集的光滑函数,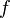 为局部可积时,它们的卷积
为局部可积时,它们的卷积 也是光滑函数。利用这一性质,对于任意的可积函数
也是光滑函数。利用这一性质,对于任意的可积函数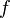 ,都可以简单地构造出一列逼近于
,都可以简单地构造出一列逼近于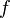 的光滑函数列
的光滑函数列 ,这种方法称为函数的光滑化或正则化。
,这种方法称为函数的光滑化或正则化。
卷积的概念还可以推广到数列、测度以及广义函数上去。
[编辑]定义
函数f 与g 的卷积记作 ,它是其中一个函数翻转并平移后与另一个函数的乘积的积分,是一个对平移量的函数。
,它是其中一个函数翻转并平移后与另一个函数的乘积的积分,是一个对平移量的函数。
积分区间取决于f 与g 的定义域。
对于定义在离散域的函数,卷积定义为
[编辑]快速卷积算法
当 ![f[n]\,](http://upload.wikimedia.org/wikipedia/zh/math/a/8/0/a80b9f5d6619a493eb3f0746f97875c1.png) 是有限长度
是有限长度 ,需要约
,需要约 次运算。借由一些快速算法可以降到
次运算。借由一些快速算法可以降到 复杂度。
复杂度。
最常见的快速卷积算法是借由圆周卷积利用快速傅里叶变换。也可借由其它不包含 FFT 的做法,如数论转换。
[编辑]多元函数卷积
按照翻转、平移、积分的定义,还可以类似的定义多元函数上的积分:
[编辑]性质
各种卷积算子都满足下列性质:
其中Df 表示f的微分,如果在离散域中则是指差分算子,包括前向差分与后向差分两种:
- 前向差分:

- 后向差分:

[编辑]卷积定理
卷积定理指出,函数卷积的傅里叶变换是函数傅里叶变换的乘积。即,一个域中的卷积相当于另一个域中的乘积,例如时域中的卷积就对应于频域中的乘积。
其中 表示f 的傅里叶变换。
表示f 的傅里叶变换。
这一定理对拉普拉斯变换、双边拉普拉斯变换、Z变换、Mellin变换和Hartley变换(参见Mellin inversion theorem)等各种傅里叶变换的变体同样成立。在调和分析中还可以推广到在局部紧致的阿贝尔群上定义的傅里叶变换。
利用卷积定理可以简化卷积的运算量。对于长度为 的序列,按照卷积的定义进行计算,需要做
的序列,按照卷积的定义进行计算,需要做 组对位乘法,其计算复杂度为
组对位乘法,其计算复杂度为 ;而利用傅里叶变换将序列变换到频域上后,只需要一组对位乘法,利用傅里叶变换的快速算法之后,总的计算复杂度为
;而利用傅里叶变换将序列变换到频域上后,只需要一组对位乘法,利用傅里叶变换的快速算法之后,总的计算复杂度为 。这一结果可以在快速乘法计算中得到应用。
。这一结果可以在快速乘法计算中得到应用。
[编辑]在群上的卷积
若 G 是有某 m 测度的群(例如豪斯多夫空间上哈尔测度下局部紧致的拓扑群),对于G 上 m-勒贝格可积的实数或复数函数f 和g,可定义它们的卷积:
对于这些群上定义的卷积同样可以给出诸如卷积定理等性质,但是这需要对这些群的表示理论以及调和分析的彼得-外尔定理。
[编辑]应用
卷积在工程和数学上都有很多应用:
- 统计学中,加权的滑动平均是一种卷积。
- 概率论中,两个统计独立变量X与Y的和的概率密度函数是X与Y的概率密度函数的卷积。
- 声学中,回声可以用源声与一个反映各种反射效应的函数的卷积表示。
- 电子工程与信号处理中,任一个线性系统的输出都可以通过将输入信号与系统函数(系统的冲激响应)做卷积获得。
- 物理学中,任何一个线性系统(符合叠加原理)都存在卷积。











 卷积是泛函分析中的重要运算,涉及函数的翻转、平移与积分。它与傅里叶变换密切相关,常用于信号处理、统计学、概率论及线性系统等领域。快速卷积算法通过FFT降低计算复杂度,卷积定理则揭示了时域与频域之间的关系。卷积还可推广到多元函数、数列、测度和广义函数上。
卷积是泛函分析中的重要运算,涉及函数的翻转、平移与积分。它与傅里叶变换密切相关,常用于信号处理、统计学、概率论及线性系统等领域。快速卷积算法通过FFT降低计算复杂度,卷积定理则揭示了时域与频域之间的关系。卷积还可推广到多元函数、数列、测度和广义函数上。

 and then offset by
t, making it
and then offset by
t, making it
 . The area under the resulting product gives the convolution at
t. The horizontal axis is
. The area under the resulting product gives the convolution at
t. The horizontal axis is
 for
f and
g, and t for
for
f and
g, and t for
 .
.

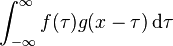

![(f \star g)[m] = \sum_n {f[n] g[m - n]}](http://upload.wikimedia.org/wikipedia/zh/math/f/b/f/fbf78d835408b40ef5900e49810101b4.png)



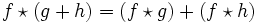

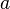 为任意
为任意


















 1348
1348

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








