2. YOLO11网络结构详细解析（以n版本为例）

置顶 已于 2025-04-29 09:02:48 修改
阅读量2.4k 收藏 43
点赞数 20
分类专栏： FXGroup：深度学习 文章标签： 算法 人工智能 深度学习
于 2025-04-23 10:01:02 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/as_grf/article/details/144801501
版权

YOLO11-n的网络结构图，如下：

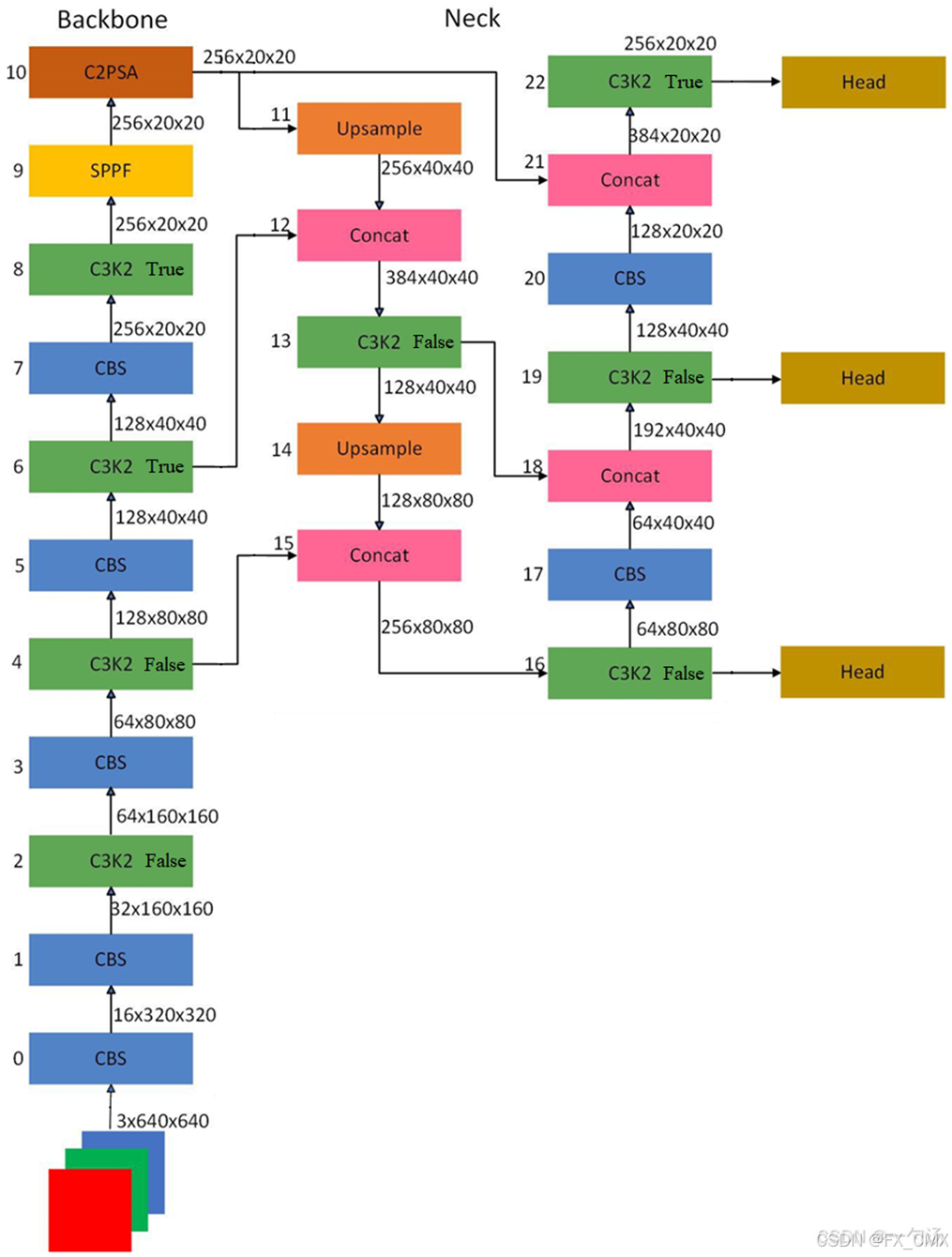
网上的关于YOLO11网格结构图，要么有错误，要么细节不清晰。这是我找到最好的版本，原图见博文：YOLO11 沉浸式讲解 YOLOV11网络结构以及代码剖析-CSDN博客

YOLO11网格结构的具体实现，可以在nn/task.py中parse_model函数显示的位置设置断点，调试过程中观察yaml文件被一行一行的解析。

具体解析如下：

YOLO11-backbone（n版本）

结构图

模块图

scales:

  # [depth, width, max_channels]

  n: [0.50, 0.25, 1024]

backbone:

  # [from, repeats, module, args]

  - [-1, 1, Conv, [64*0.25, 3, 2]] # 0-P1/2

  - [-1, 1, Conv, [128*0.25, 3, 2]] # 1-P2/4

  - [-1, 2*0.50, C3k2, [256*0.25, False, 0.25]]

  - [-1, 1, Conv, [256*0.25, 3, 2]] # 3-P3/8

  - [-1, 2*0.50, C3k2, [512*0.25, False, 0.25]]

  - [-1, 1, Conv, [512*0.25, 3, 2]] # 5-P4/16

  - [-1, 2*0.50, C3k2, [512*0.25, True]]

  - [-1, 1, Conv, [1024*0.25, 3, 2]] # 7-P5/32

  - [-1, 2*0.50, C3k2, [1024*0.25, True]]

  - [-1, 1, SPPF, [1024*0.25, 5]] # 9

  - [-1, 2*0.50, C2PSA, [1024*0.25]] # 10

CBS:

 

Bottleneck:

C3K:

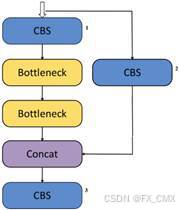
C3K2(False):

 

C3K2(True):

 SPPF:

 

C2PSA:  

YOLO11-backbone

层号

说明

  - [-1, 1, Conv, [64*0.25, 3, 2]] # 0-P1/2

0

640→320, c1=3, c2=64*0.25=16, CBS: k=3 s=2

  - [-1, 1, Conv, [128*0.25, 3, 2]] # 1-P2/4

1

320→160, c1=16, c2=128*0.25=32, CBS: k=3 s=2

  - [-1, 2*0.5, C3k2, [256*0.25, False, 0.25]]

2

160→160, c1=32, c2=256*0.25=64, e=0.25,

C3K2(False):

    第1个CBS: cin=c1=32, cout=c2*e*2=32, k=1 s=1

    Split: 2个c=c2*e=16

    Bottleneck: n=2*0.5=1个, cin=cout=c=16, shortcut=true, 2个CBS:

        第1个CBS: cin=16, cout=16*0.5=8, k=3 s=1

        第2个CBS: cin=16*0.5=8, cout=16, k=3 s=1

    Concat: (2+n)*c=48

    第2个CBS: cin=(2+n)*c=48, cout=c2=64, k=1 s=1

  - [-1, 1, Conv, [256*0.25, 3, 2]] # 3-P3/8

3

160→80, c1=64, c2=256*0.25=64, CBS: k=3 s=2

  - [-1, 2*0.5, C3k2, [512*0.25, False, 0.25]]

4

80→80, c1=64, c2=512*0.25=128, e=0.25,

C3K2(False):

    第1个CBS: cin=c1=64, cout=c2*e*2=64, k=1 s=1

    Split: 2个c=c2*e=32

    Bottleneck: n=2*0.5=1, cin=cout=c=32, shortcut=true, 2个CBS:

        第1个CBS: cin=32, cout=32*0.5=16, k=3 s=1

        第2个CBS: cin=32*0.5=16, cout=32, k=3 s=1

    Concat: (2+n)*c=96

    第2个CBS: cin=(2+n)*c=96, cout=c2=128, k=1 s=1

  - [-1, 1, Conv, [512*0.25, 3, 2]] # 5-P4/16

5

80→40, c1=128, c2=512*0.25=128, CBS: k=3 s=2

  - [-1, 2*0.5, C3k2, [512*0.25, True]]

6

40→40, c1=128, c2=512*0.25=128, e=0.5(默认值),

C3K2(True):

    第1个CBS: cin=c1=128, cout=c2*e*2=128, k=1 s=1

    Split: 2个c=c2*e=64

    C3K: n=2*0.5=1, cin=cout=c=64, shortcut=true

        CBS-1: cin=c=64, cout=c*e=32, k=1 s=1

        CBS-2: cin=c=64, cout=c*e=32, k=1 s=1

        2个Bottleneck: cin=c*e=32, cout= c*e=32, shortcut=true

            第1个CBS: cin= c*e=32, cout= c*e =32, k=3 s=1

            第2个CBS: cin= c*e =32, cout= c*e=32, k=3 s=1

        Concat: c*e + c*e=64

        CBS-3: cin= c*e + c*e=64, cout=c=64, k=1 s=1

    Concat: (2+n)*c=192

    第2个CBS: cin=(2+n)*c=192, cout=c2=128, k=1 s=1

  - [-1, 1, Conv, [1024*0.25, 3, 2]] # 7-P5/32

7

40→20, c1=128, c2=1024*0.25=256, CBS: k=3 s=2

  - [-1, 2*0.5, C3k2, [1024*0.25, True]]

8

20→20, c1=256, c2=1024*0.25=256, e=0.5(默认值),

C3K2(True):

    第1个CBS: cin=c1=256, cout=c2*e*2=256, k=1 s=1

    Split: 2个c=c2*e=128

    C3K: n=2*0.5=1, cin=cout=c=128, shortcut=true

        CBS-1: cin=c=128, cout=c*e=64, k=1 s=1

        CBS-2: cin=c=128, cout=c*e=64, k=1 s=1

        2个Bottleneck: cin=c*e=64, cout= c*e=64, shortcut=true

            第1个CBS: cin= c*e=64, cout= c*e =64, k=3 s=1

            第2个CBS: cin= c*e =64, cout= c*e=64, k=3 s=1

        Concat: c*e + c*e=128

        CBS-3: cin= c*e + c*e=128, cout=c=128, k=1 s=1

    Concat: (2+n)*c=384

    第2个CBS: cin=(2+n)*c=384, cout=c2=256, k=1 s=1

  - [-1, 1, SPPF, [1024*0.25, 5]] # 9

9

20→20, c1=256, c2=1024*0.25=256, k=5,

SPPF:

  第1个CBS: cin=c1=256, cout=c1/2=128, k=1 s=1

  MaxPool2d: k=5, s=1, p=2

  Concat: (c1/2)*4=512

  第2个CBS: cin=(c1/2)*4=512, cout=c2=256, k=1 s=1

  - [-1, 2*0.5, C2PSA, [1024*0.25]] # 10

10

20→20, c1=256, c2=1024*0.25=256,

C2PSA:

    第1个CBS: cin=c1=256, cout=256, k=1 s=1

    Split: 2个c=c1*0.5=128

    PSABlock: n=2*0.5=1,

        Attention: cin=c=128, cout=128, shortcut=true

        FNN: cin=c=128, cout=128, shortcut=true

            第1个CBS: cin=128, cout=256, k=1 s=1

            第2个CBS: cin=256, cout=128, k=1 s=1

    Concat: 128+128=256

    第2个CBS: cin =256, cout=256, k=1 s=1

YOLO11-head

结构图

head:

  - [-1, 1, nn.Upsample, [None, 2, "nearest"]]

  - [[-1, 6], 1, Concat, [1]] # cat backbone P4

  - [-1, 2*0.5, C3k2, [512*0.25, False]] # 13

  - [-1, 1, nn.Upsample, [None, 2, "nearest"]]

  - [[-1, 4], 1, Concat, [1]] # cat backbone P3

  - [-1, 2*0.5, C3k2, [256*0.25, False]] # 16 (P3/8-small)

  - [-1, 1, Conv, [256*0.25, 3, 2]]

  - [[-1, 13], 1, Concat, [1]] # cat head P4

  - [-1, 2*0.5, C3k2, [512*0.25, False]] # 19 (P4/16-medium)

  - [-1, 1, Conv, [512*0.25, 3, 2]]

  - [[-1, 10], 1, Concat, [1]] # cat head P5

  - [-1, 2*0.5, C3k2, [1024*0.25, True]] # 22 (P5/32-large)

YOLO11-head

层号

说明

  - [-1, 1, nn.Upsample, [None, 2, "nearest"]]

11

20→40, c1=256, c2=256

Upsample(scale_factor=2.0, mode='nearest')

  - [[-1, 6], 1, Concat, [1]] # cat backbone P4

12

40→40, c1=128+256, c2=384

  - [-1, 2*0.5, C3k2, [512*0.25, False]] # 13

13

40→40, c1=384, c2=512*0.25=128, e=0.5(默认值),

C3K2(False):

    第1个CBS: cin=c1=384, cout=c2*e*2=128, k=1 s=1

    Split: 2个c=c2*e=64

    Bottleneck: n=2*0.5=1个, cin=cout=c=64, shortcut=true, 2个CBS:

        第1个CBS: cin=64, cout=64*0.5=32, k=3 s=1

        第2个CBS: cin=64*0.5=32, cout=64, k=3 s=1

    Concat: (2+n)*c=192

    第2个CBS: cin=(2+n)*c=192, cout=c2=128, k=1 s=1

  - [-1, 1, nn.Upsample, [None, 2, "nearest"]]

14

40→80, c1=128, c2=128

Upsample(scale_factor=2.0, mode='nearest')

  - [[-1, 4], 1, Concat, [1]] # cat backbone P3

15

80→80, c1=128+128, c2=256

  - [-1, 2*0.5, C3k2, [256*0.25, False]] # 16 (P3/8-small)

16

80→80, c1=256, c2=256*0.25=64, e=0.5(默认值),

C3K2(False):

    第1个CBS: cin=c1=256, cout=c2*e*2=64, k=1 s=1

    Split: 2个c=c2*e=32

    Bottleneck: n=2*0.5=1个, cin=cout=c=32, shortcut=true, 2个CBS:

        第1个CBS: cin=32, cout=32*0.5=16, k=3 s=1

        第2个CBS: cin=32*0.5=16, cout=32, k=3 s=1

    Concat: (2+n)*c=96

    第2个CBS: cin=(2+n)*c=96, cout=c2=64, k=1 s=1

  - [-1, 1, Conv, [256*0.25, 3, 2]]

17

80→40, c1=64, c2=256*0.25=64, CBS: k=3 s=2

  - [[-1, 13], 1, Concat, [1]] # cat head P4

18

40→40, c1=128+64, c2=192

  - [-1, 2*0.5, C3k2, [512*0.25, False]] # 19 (P4/16-medium)

19

40→40, c1=192, c2=512*0.25=128, e=0.5(默认值),

C3K2(False):

    第1个CBS: cin=c1=192, cout=c2*e*2=128, k=1 s=1

    Split: 2个c=c2*e=64

    Bottleneck: n=2*0.5=1个, cin=cout=c=64, shortcut=true, 2个CBS:

        第1个CBS: cin=64, cout=64*0.5=32, k=3 s=1

        第2个CBS: cin=64*0.5=32, cout=64, k=3 s=1

    Concat: (2+n)*c=192

    第2个CBS: cin=(2+n)*c=192, cout=c2=128, k=1 s=1

  - [-1, 1, Conv, [512*0.25, 3, 2]]

20

40→20, c1=128, c2=512*0.25=128, CBS: k=3 s=2

  - [[-1, 10], 1, Concat, [1]] # cat head P5

21

20→20, c1=128+256, c2=384

  - [-1, 2*0.5, C3k2, [1024*0.25, True]] # 22 (P5/32-large)

22

20→20, c1=384, c2=1024*0.25=256, e=0.5(默认值),

C3K2(True):

    第1个CBS: cin=c1=384, cout=c2*e*2=256, k=1 s=1

    Split: 2个c=c2*e=128

    C3K: n=2*0.5=1, cin=cout=c=128, shortcut=true

        CBS-1: cin=c=128, cout=c*e=64, k=1 s=1

        CBS-2: cin=c=128, cout=c*e=64, k=1 s=1

        2个Bottleneck: cin=c*e=64, cout= c*e=64, shortcut=true

            第1个CBS: cin= c*e=64, cout= c*e =64, k=3 s=1

            第2个CBS: cin= c*e =64, cout= c*e=64, k=3 s=1

        Concat: c*e + c*e=128

        CBS-3: cin= c*e + c*e=128, cout=c=128, k=1 s=1

    Concat: (2+n)*c=384

    第2个CBS: cin=(2+n)*c=384, cout=c2=256, k=1 s=1

yolov11 项目结构
weixin_50993868的博客
03-25 53
YOLO网络架构
YOLOv11(ultralytics新作品-YOLOv8后续) | 一文带你深入理解yolov11全部内容（附网络结构图）
qq_41304809的博客
11-01 1万+
YOLOv11 是 Ultralytics 推出的最新的集目标检测、语义分割、图像分类等任务于一体的神经网络，其基本原理涉及到主干网络、颈部网络（neck）、检测头等部分，以下是详细介绍：变化1：C2f模块更换成了C3k2模块；变化2：在第九层SPPF之后，YOLOv11加上了一层C2PSA模块；变化三：在检测部分，YOLOv11也替换了C2F模块为C3K2模块；并且检测头内卷积更换成了深度可分离卷积下面详细介绍这三个变化：首先，第一个变化的C3k2模块其实并没有改变网络结构，其网络结构与C2F还是一样的，
YOLO系列结构图-visio
03-08
1.YOLOV3 2.YOLOV4 3.YOLOV5
YOLOv11网络结构
qq_54488514的博客
10-01 1万+
YOLOv11震撼来袭
YOLOv11 技术架构与模块解析
最新发布
weixin_43199439的博客
04-07 264
YOLOv11 作为 YOLO 系列演进的新版本，在保持 One-Stage 快速检测体系的前提下，引入多个结构创新模块，旨在平衡精度与速度之间的矛盾。
YOLO11 沉浸式讲解 YOLOV11网络结构以及代码剖析
qq_64693987的博客
10-01 6万+
YOLO11采用改进的骨干和颈部架构，增强了特征提取能力，提高了物体检测的精确度和复杂任务的表现。YOLO11引入精炼的架构设计和优化的训练流程，实现更快的处理速度，同时保持精度和性能之间的最佳平衡。通过模型设计的进步，YOLO11m在COCO数据集上实现了更高的均值平均精度（mAP），同时使用比YOLOv8m少22%的参数，使其在不妥协准确性的情况下更加计算高效。YOLO11可以无缝部署在各种环境中，包括边缘设备、云平台以及支持NVIDIA GPU的系统，确保最大灵活性。
YOLOv11来了，使用YOLOv11训练自己的数据集和推理(附YOLOv11网络结构图)
热门推荐
在职AI算法工程师，擅长计算机视觉，YOLO目标检测、分割等，擅长web、pyqt界面可视化，好内容持续更新中，来这里跟大家一起学习，共同进步
10-02 16万+
YOLOv11 由 Ultralytics 在 2024 年 9 月 30 日发布， 最新的 YOLOv11 模型在之前的 YOLO 版本引入了新功能和改进，以进一步提高性能和灵活性。YOLO11 在快速、准确且易于使用，使其成为各种对象检测和跟踪、实例分割、图像分类和姿态估计任务的绝佳选择。
Yolo11网络结构详解与对比
m0_64913373的博客
09-30 6943
可以发现，引入了自注意力机制，首先使用了卷积块提取特征，并分为两部分a,b,其中b会通过PSAblock进行注意力计算，最后再通过cat与a连接，并用一个卷积进一步提取特征。可以看到，相比于C2f，当超参数c3k=True时，瓶颈块替换为 C3k，否则还是C2f,而C3k相比于C3则是可以让使用者自定义卷积块大小，更加灵活。而在PSAblock中，则是使用了多头注意力和一个前馈神经网络ffn，ffn是通过两个1*1的卷积层实现的最后通过超参数判断是否残差连接，最后返回结果。
YOLOv10 | 手把手教你利用yolov10训练自己数据集（含环境搭建、参数解析 、数据集查找、模型训练、推理、导出）
Snu77的博客
05-26 3万+
本文内含YOLOv10网络结构图 + 各个创新模块手撕结构图 + 训练教程 + 推理教程 + 参数解析 + 环境搭建 + 数据集获取等一些有关YOLOv10的内容！目录一、前言二、整体网络结构图三、空间-通道分离下采样3.1 SCDown介绍3.2 C2fUIB介绍3.3 PSA介绍四、环境搭建五、数据集获取六、模型获取七、模型训练7.1 训练的三种方式7.1.1 方式一7.1.2 方式二（推荐）7.1.3 方式三八、模型验证/测试九、模型推理十、模型输出官方论文地址点击此处即可跳转。
YOLOv11一文弄懂 | YOLOv11网络结构解读 、yolov11.yaml配置文件详细解读与说明、模型训练参数详细解析 | 通俗易懂！入门必看系列！
qq_45972324的博客
12-22 3万+
YOLOv11是由Ultralytics公司开发的新一代目标检测算法，它在之前YOLO版本的基础上进行了显著的架构和训练方法改进。整合了改进的模型结构设计增强的特征提取技术和优化的训练方法。真正让YOLO11脱颖而出的是它令人印象深刻的速度准确性和效率的结合，使其成为Ultralytics迄今为止创造的最强大的型号之一。通过改进设计，YOLO11提供了更好的特征提取，这是从图像中识别重要模式和细节的过程，即使在具有挑战性的场景中，也可以更准确地捕捉复杂的方面。
YOLOv11训练自己的数据集，从代码下载到实例测试 （含YOLOv11网络结构图）
Limiiiing的博客
09-30 2万+
在Windows10上配置CUDA环境教程2024年9月30日，YOLOv11是最新发布的计算机视觉模型。支持多种任务，包括目标检测、实例分割、图像分类、姿态估计、有向目标检测以及物体跟踪等，本文主要讲述其检测任务的模型搭建训练流程。以上就是YOLOv11训练自己数据集的全部过程啦，欢迎大家在评论区交流~
yolo v3的网络结构
12-25
yolo v3的网络结构，用于目标检测，语义分割，内容较多，此处仅仅只是其网络结构。
YOLOv11 | 一文带你深入理解ultralytics最新作品yolov11的创新 | 训练、推理、验证、导出 （附网络结构图）
Snu77的博客
10-01 13万+
ultralytics发布了最新的作品YOLOv11，这一次YOLOv11的变化相对于ultralytics公司的上一代作品YOLOv8变化还是很大的（YOLOv9、YOLOv10均不是ultralytics公司作品），其中改变的位置涉及到C2f变为C3K2，在SPPF后面加了一层类似于注意力机制的C2PSA，还有一个变化大家从yaml文件是看不出来的就是它的检测头内部替换了两个DWConv，在损失函数方面就没有变化了还是采用的CIoU作为边界框回归损失，下面带大家深入理解一下ultralytics最新作品
YOLOv11改进 | 网络结构代码逐行解析(三) | 从yaml文件到网络结构解析到模型定义
Snu77的博客
10-21 5087
本文给大家带来的是YOLOv11项目的解读，之前给大家分析了YOLOv11的项目文件分析，这一篇文章给大家带来的是模型训练从我们的yaml文件定义到模型的定义部分的讲解，我们一般只知道如何去训练模型，和配置yaml文件，但是对于yaml文件是如何输入到模型里，模型如何将yaml文件解析出来的确是不知道的，本文的内容接上一篇的代码逐行解析(一) 项目目录分析，本文对于小白来说非常友好，非常推荐大家进行阅读，深度的了解模型的工作原理已经流程，下面我们从yaml文件来讲解。
YOLO11改进 | Head | 增加网络结构增强小目标检测能力【独家创新——附结构图】
kay_545
10-31 2054
yolo11改进，yolo11，小目标检测
万字详解YOLOv8网络结构Backbone/neck/head以及Conv、Bottleneck、C2f、SPPF、Detect等模块
专注于图像领域，主要研究内容包括计算机视觉和深度学习，特别是在图像分类、目标检测和图像生成等方面有深入的研究和实践经验。
05-26 8万+
YOLOv8是由Ultralytics开发的最先进的目标检测模型，推升了速度、准确性和用户友好性的界限。YOLO这一缩写代表“你只看一次”（You Only Look Once），通过在一次网络传递中同时预测所有边界框，提升了算法的效率和实时处理能力。相比之下，其他一些目标检测技术需要经过多个阶段或过程来完成检测。YOLOv8在流行的YOLOv5架构上进行了扩展，在多个方面提供了改进。
YOLO11改进 | 主干网络 | 将backbone替换为MobileNetV4【小白必备教程+附完整代码】
kay_545
10-24 2401
yolo11改进，yolo11，MobileNetV4
目标检测算法-YOLOV11解析
10-24 1万+
YOLOv11是由Ultralytics公司开发的新一代目标检测算法，它在之前YOLO版本的基础上进行了显著的架构和训练方法改进。整合了。
YOLOv11对比YOLOV8网络结构变化分析，帮助你真正的理解和学习yolo框架
qq_39128381的博客
10-15 1万+
yolov11 yolo
yolo网络结构图怎么下
03-26
### 如何获取 YOLO 网络结构图 要获取 YOLO 网络结构图，可以通过以下几种方式实现： #### 方法一：直接查找官方文档或论文中的图片 许多关于 YOLO 的研究都附带详细的网络结构图。这些图像通常可以在原始论文或者相关技术博客中找到。例如，在 YOLO 官方 GitHub 页面以及学术文章中，作者经常提供清晰的网络架构图[^1]。 如果需要高分辨率版本，可以尝试访问原作者发布的资源页面，或者查阅引用的相关资料，比如【YOLO系列】YOLO v3（网络结构图+代码）、【YOLO 系列】YOLO v4-v5先验知识等。 #### 方法二：利用绘图工具自行制作 对于更灵活的需求，可以选择使用专业的绘图软件来重新创建网络结构图。Visio 是一种常用的流程图设计工具，能够帮助用户按照需求调整并绘制复杂的神经网络结构。具体操作方法可参考有关教程，如通过 Visio 绘制 YOLOv8 和 YOLOv11 的网络结构图[^2]。 以下是简单的 Python 脚本用于生成基础的可视化图表（仅作为辅助手段），虽然它无法完全替代高质量的手动绘制效果，但在快速预览时非常有用： ```python import matplotlib.pyplot as plt from tensorflow.keras.utils import plot_model from tensorflow.keras.models import Sequential from tensorflow.keras.layers import Conv2D, MaxPooling2D, Flatten, Dense model = Sequential([ Conv2D(32, (3, 3), activation='relu', input_shape=(224, 224, 3)), MaxPooling2D((2, 2)), Conv2D(64, (3, 3), activation='relu'), MaxPooling2D((2, 2)), Flatten(), Dense(10, activation='softmax') ]) plot_model(model, to_file="yolo_structure.png", show_shapes=True) plt.show() ``` 此脚本会保存一张名为 `yolo_structure.png` 的文件到当前目录下，显示的是简化版卷积层和全连接层之间的关系示意图。 #### 方法三：在线搜索引擎查询公开素材 最后还可以借助 Google 图片搜索功能输入关键词 “YOLO network architecture diagram”，即可浏览大量已有的现成成果供下载选用。 ---
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值