PCL中GreedyProjection三角化算法简介与示例

---

---

前言

Delaunay三角剖分最初应用于2维领域，而与Greedy三角化算法的结合，使之成为目前在三维重建领域最为基础的算法原理之一，很多学者针对其原理进行改进用以三维点云模型的构建。

---

一、PCL点云三角化

1.1 Delaunay三角剖分

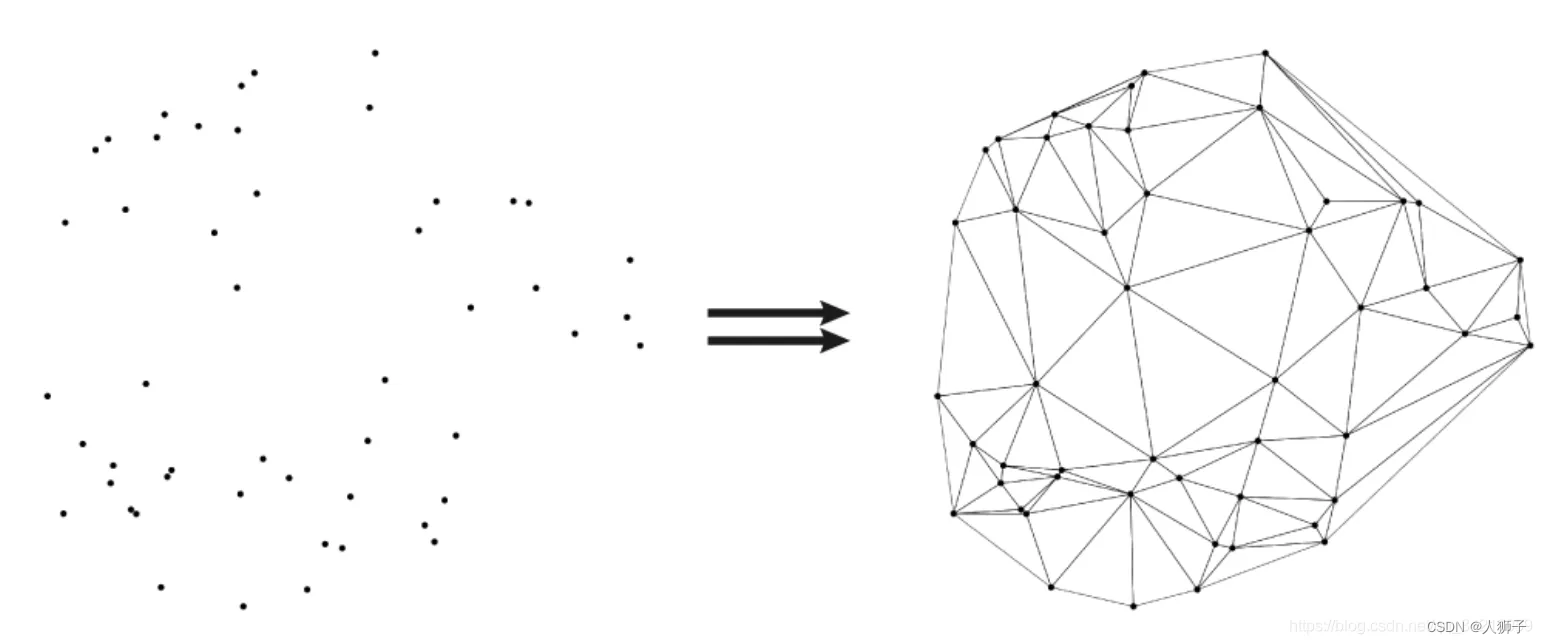
定义：假设点集中的一条边e（两个端点为a,b），e若满足下列条件，则称之为Delaunay边：存在一个圆经过a,b两点，圆内(圆上最多三点共圆)不含点集中任何其他的点。而Delaunay三角化就是指三角网格均是由Delaunay边组成，并满足最小角最大原则（在点集可能形成的三角剖分中，Delaunay三角剖分所形成的三角形的最小角最大）。

针对以上定义，目前已提出了很多经典的剖分算法，如Lawson算法、Bowyer-Watson算法。以上算法都很有意思，通过点插法实现，具体原理可以查看以下链接。
技术分享：Delaunay三角剖分算法介绍

1.2 贪婪三角化

PCL中采用将三维点云投影到二维平面的方法来实现三角剖分， 具体采用贪婪三角化算法。
其过程为：
1：计算点云中点的法线，再将点云通过法线投影到二维坐标平面。
2：使用基于Delaunay三角剖分的空间区域增长算法完成平面点集的三角化。
3：根据投影点云的连接关系确定原始三维点云间的拓扑关系，最终得到曲面模型。

PCL中的NormalEstimation和GreedyProjectionTriangulation类实现该计算过程。
源代码：

FFN和SFN是指两个不同方向的边缘邻域集，在connectPoint方法里完成计算。

/** \brief Index of the current query point **/
int R_;

std::vector<int> ffn_;
std::vector<int> sfn_;

// Locating FFN and SFN to adapt distance threshold
      double sqr_source_dist = (coords_[R_] - coords_[source_[R_]]).squaredNorm ();
      double sqr_ffn_dist = (coords_[R_] - coords_[ffn_[R_]]).squaredNorm ();
      double sqr_sfn_dist = (coords_[R_] - coords_[sfn_[R_]]).squaredNorm ();
      double max_sqr_fn_dist = (std::max)(sqr_ffn_dist, sqr_sfn_dist);
      double sqr_dist_threshold = (std::min)(sqr_max_edge, sqr_mu * sqrDists[1]); //sqr_mu * sqr_avg_conn_dist);
      if (max_sqr_fn_dist > sqrDists[nnn_-1])
      {
        if (0 == increase_nnn4fn)
          PCL_WARN("Not enough neighbors are considered: ffn or sfn out of range! Consider increasing nnn_... Setting R=%d to be BOUNDARY!\n", R_);
        increase_nnn4fn++;
        state_[R_] = BOUNDARY;
        continue;
      }
      double max_sqr_fns_dist = (std::max)(sqr_source_dist, max_sqr_fn_dist);
      if (max_sqr_fns_dist > sqrDists[nnn_-1])
      {
        if (0 == increase_nnn4s)
          PCL_WARN("Not enough neighbors are considered: source of R=%d is out of range! Consider increasing nnn_...\n", R_);
        increase_nnn4s++;
      }

计算法线：

// Get the normal estimate at the current point 
const Eigen::Vector3f nc = (*input_)[(*indices_)[R_]].getNormalVector3fMap ();

三角化：

// Triangulating
      if (angles_[2].visible == false)
      {
        if ( !( (angles_[0].index == ffn_[R_] && angles_[1].index == sfn_[R_]) || (angles_[0].index == sfn_[R_] && angles_[1].index == ffn_[R_]) ) )
        {
          state_[R_] = BOUNDARY;
        }
        else
        {
          if ((source_[R_] == angles_[0].index) || (source_[R_] == angles_[1].index))
            state_[R_] = BOUNDARY;
          else
          {
            if (sqr_max_edge < (coords_[ffn_[R_]] - coords_[sfn_[R_]]).squaredNorm ())
            {
              state_[R_] = BOUNDARY;
            }
            else
            {
              tmp_ = coords_[source_[R_]] - proj_qp_;
              uvn_s[0] = tmp_.dot(u_);
              uvn_s[1] = tmp_.dot(v_);
              double angleS = std::atan2(uvn_s[1], uvn_s[0]);
              double dif = angles_[1].angle - angles_[0].angle;
              if ((angles_[0].angle < angleS) && (angleS < angles_[1].angle))
              {
                if (dif < 2*M_PI - maximum_angle_)
                  state_[R_] = BOUNDARY;
                else
                  closeTriangle (polygons);
              }
              else
              {
                if (dif >= maximum_angle_)
                  state_[R_] = BOUNDARY;
                else
                  closeTriangle (polygons);
              }
            }
          }
        }
        continue;
      }

源码中大量代码关注于三角形的连接问题。
最后调用MeshConstruction类的reconstruct方法进行表面重建。

template <typename PointInT> void
MeshConstruction<PointInT>::reconstruct (std::vector<pcl::Vertices> &polygons)
{
  if (!initCompute ())
  {
    polygons.clear ();
    return;
  }

  // Check if a space search locator was given
  if (check_tree_)
  {
    if (!tree_)
    {
      if (input_->isOrganized ())
        tree_.reset (new pcl::search::OrganizedNeighbor<PointInT> ());
      else
        tree_.reset (new pcl::search::KdTree<PointInT> (false));
    }

    // Send the surface dataset to the spatial locator
    tree_->setInputCloud (input_, indices_);
  }

  // Set up the output dataset
  //polygons.clear ();
  //polygons.reserve (2 * indices_->size ()); /// NOTE: usually the number of triangles is around twice the number of vertices
  // Perform the actual surface reconstruction
  performReconstruction (polygons);

  deinitCompute ();
}

二、程序示例

//----------------------------------法线计算-----------------------------------
    pcl::NormalEstimation<pcl::PointXYZ, pcl::Normal> n;
    pcl::PointCloud<pcl::Normal>::Ptr normals(new pcl::PointCloud<pcl::Normal>);
    pcl::search::KdTree<pcl::PointXYZ>::Ptr tree1(new pcl::search::KdTree<pcl::PointXYZ>);
    tree->setInputCloud(cloud);
    
    n.setInputCloud(cloud);
    n.setSearchMethod(tree1);
    n.setKSearch(20);
    n.compute(*normals);
    
    pcl::PointCloud<pcl::PointNormal>::Ptr cloud_with_normals(new pcl::PointCloud<pcl::PointNormal>);
    pcl::concatenateFields(*cloud, *normals, *cloud_with_normals);//连接点云和法线
    pcl::search::KdTree<pcl::PointNormal>::Ptr tree2(new pcl::search::KdTree<pcl::PointNormal>);
    tree2->setInputCloud(cloud_with_normals);
    
    pcl::GreedyProjectionTriangulation<pcl::PointNormal> gp;
    pcl::PolygonMesh triangles;
    
    gp.setSearchRadius(0.025);//设置搜索半径，即连接点的最大距离
    gp.setMu(2.5); //加权因子，对于每个样本点，其映射所选球的半径由mu与离样本点最近点的距离乘积决定，用以解决点云密度不均匀的问题，mu一般取值2.5-3
    gp.setMaximumNearestNeighbors(600); //最大领域点个数
    gp.setMaximumSurfaceAngle(M_PI / 4);//临近点的法线和样本点法线的最大偏离角度
    gp.setMinimumAngle(M_PI / 18); //三角形最小角
    gp.setMaximumAngle(2 * M_PI / 3);//三角形最大角
    gp.setNormalConsistency(false); //保证法线朝向一致
    gp.setInputCloud(cloud_with_normals);
    gp.setSearchMethod(tree2);   
    gp.reconstruct(triangles);

总结

彻底理解三角化的源代码比较困难，缺少相关学习资料，欢迎共同研究，提出意见。