归一化原来这么重要！深入浅出详解Transformer中的Normalization

©PaperWeekly 原创 · 作者 | 李国趸

单位 | 浙江大学

研究方向 | 少样本学习

为了讲清楚 Transformer 中的归一化细节，我们首先需要了解下，什么是归一化，以及为什么要归一化。本文主要解决这两个问题：

• 什么是归一化？

• 为什要归一化？

从函数的等高线说起

1.1 函数的等高线是什么

讨论一个二元损失函数的情况，即损失函数只有两个参数： 。

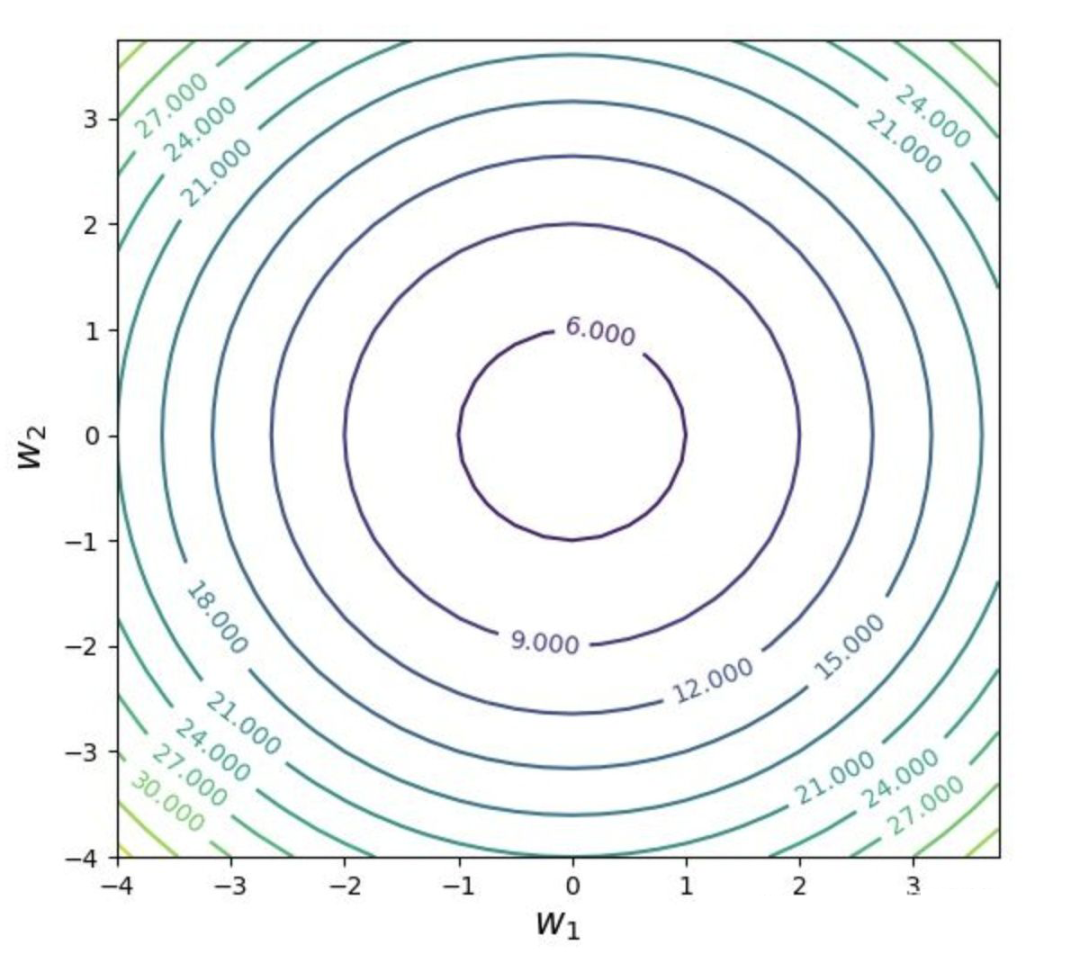
• 下图就是这个损失函数的图像，等高线就是函数 在参数平面 上的投影。

• 等高的理解：在投影面上的任意一个环中，所有点的函数值都一样。

• 等高的理解：在函数曲面上存在一个环，环上所有点的函数值一样，即距离投影平面的距离都一样。

具体看这个参数平面的话，绘制等高线图是：

• 任意一个环上的不同参数取值 ，其函数值都一样。

• 可以看到，当 时，函数值 = 5，即全局最小点。

1.2 梯度与等高线的关系

假设存在一个损失函数 ，在空间中是一个曲面，当其被一个平面 ，c 为常数所截后，得到的曲线方程是：

曲线在 xoy 平面上的投影是一个平面曲线，即 ，即损失函数在 xoy 平面的某一条等高线，在这条等高线上，所有函数值均为 。

在这条等高线上，任意一点的切线斜率为 。

由隐函数存在定理：

可知： 

任意一点的法线由于和切线垂直，所以斜率相乘为 -1，则法线斜率为：

又由梯度的定义：

梯度向量的斜率，即正切值= ，可以看到恰好等于法线的斜率，因此：

梯度的方向和等高线上的切线时时垂直。

1.3 从等高线看为什么特征归一化

采用梯度下降算法时，因为梯度的方向和等高线的切线是垂直的，所以沿着梯度反方向迭代时，实际就是垂直于等高线一步步迭代。如下图所示，这是两种不同的等高线采用梯度下降算法时的迭代情况。很明显，左图也就是等高线呈现正圆形时能够有最少的迭代步数，因此收敛速度更快。然而在有些情况下，等高线是椭圆形的，会有更多的迭代步数才能到达函数最低点，收敛变慢。

那么，什么时候会出现这种椭圆形的等高线情况呢？我们对线性回归和逻辑回归分别进行分析。

以线性回归为例，假设某线性回归模型为：

目标函数为（忽略偏置）：

从上式可以看出，由于 ，那么当 产生相同的增量时，后者能产生更大的函数变化值，从而产生椭圆形的环状等高线。本质上，这是因为输入的特征的尺度（即取值范围）不一样！

因此，在线性回归中若各个特征变量之间的取值范围差异较大，则会导致目标函数收敛速度慢等问题，需要对输入特征进行归一化，尽量避免形成椭圆形的等高线。

以逻辑回归为例，由于逻辑回归中特征组合的加权和还会作用上 sigmoid 函数，影响收敛的因素，除了梯度下降算法的效率外，更重要的是最后的输出 z 的大小的影响。

从上图可以看出，当z的值小于 -5 左右时，函数值约等于 0，当 z 的值大于 5 左右时，函数值约等于 1。这两种情况下面，梯度趋近于 0，使得参数无法得到更新。因此，对于逻辑回归来说，主要影响的是特征组合加权和后的 sigmoid 输出，而特征的输入范围又会影响最终的 sigmoid 输出，影响模型的收敛性，所以要对输入特征进行归一化，避免最后的输出处于梯度饱和区。

1.4 总结

总结来说，输入特征的尺度会影响梯度下降算法的迭代步数以及梯度更新的难度，从而影响训练的收敛性。

因此，我们需要对特征进行归一化，即使得各个特征有相似的尺度。

常见的特征归一化

上文我们讲了特征归一化，就是要让各个特征有相似的尺度。相似的尺度一般是讲要有相似的取值范围。因此我们可以通过一些方法把特征的取值范围约束到一个相同的区间。另一方面，这个尺度也可以理解为这些特征都是从一个相似的分布中采样得来。因此我们还可以通过一些方法使得不同特征的取值均符合相似的分布。

这里我们介绍一些常见的特征归一化方法的细节，原理和实现。

2.1 细节

rescaling (min-max normalization, range scaling)

这里是把每一维的值都映射到目标区间 。一般常用的目标区间是 。特别的，映射到 0 和 1 区间的的计算方式为：

402 Payment Required

。

mean normalization

。这里 指的向量的均值。与上面不同的是，这里减去的是均值。这样能够保证向量中所有元素的均值为 0。

standard normalization (z-score normalization)

。这里 指的是向量的标准差。更常见的是这种，使得所有元素的均值为 0，方差为 1。

scaling to unit length

。这里是把向量除以其长度，即对向量的长度进行归一化。长度度量一般采用 L1 范数或者 L2 范数。

范数（英语：Norm），是具有“长度”概念的函数。在线性代数、泛函分析及相关的数学领域，是一个函数，其为向量空间内的所有向量赋予非零的正长度或大小。Lp(p=1..n) 范数：

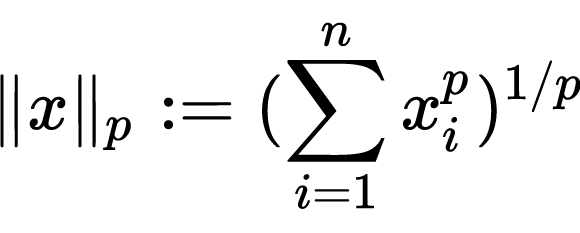
2.2 原理

总结来看，前三种特征归一化方法的计算方式是减一个统计量再除以一个统计量，最后一种为除以向量自身的长度。

减去一个统计量可以看做选哪个值作为原点（是最小值或者均值），然后将整个数据集都平移到这个新的原点位置。如果特征之间的偏置不同会对后续过程产生负面影响，则该操作是有益的，可以看做某种偏置无关操作。如果原始特征值是有特殊意义的，则该操作可能会有害。

如何理解：对于一堆二维数据，计算均值得到 (a,b)，减去这个均值点，就相当于把整个平面直角坐标系平移到这个点上，为什么呢？因为 (a,b)-(a,b)=(0,0) 就是原点，其他的点在 x 轴和 y 轴上做相应移动。

除以一个统计量可以看做在坐标轴方向上对特征进行缩放，用于降低特征尺度的影响，可以看做某种特征无关操作。缩放可以采用最大值和最小值之间的跨度，也可以用标准差（到中心点的平均距离）。

如何理解：(a,b)/3=(a/3, b/3)，就相当于这些点在 x 轴上的值缩小三倍，在 y 轴上缩小三倍。

除以长度相当于把长度归一化，把所有特征都映射到单位球上，可以看作某种长度无关操作。比如词频特征要移除文章长度的影响，图像处理中某些特征要移除光照强度的影响，以及方便计算向量余弦相似度等。

如何理解：除以向量的模，实际就是让向量的长度为 1，这样子，若干个 n 维向量就分布在一个单位球上，只是方向不同。

更直观地，可以从下图（来自于 CS231n 课程）观察上述方法的作用。下图是一堆二维数据点的可视化，可以看到，减去了每个维度的均值 以后，数据点的中心移动到了原点位置，进一步的，每个维度用标准差缩放以后，在每个维度上，数据点的取值范围均保持相同。

2.3 实现

上面我们讲了 4 种不同的归一化方式，