OPENCV之从calibrateCamera到solvePnP（二）

接上一篇。

看函数

第一个参数和第二个参数与上一篇类似，不过上一篇的是多幅图的多组点，类型为双重vector，这里是一副图中的一组点，类型为单重vector。

vector<Point3f> calcBoardCornerPositions(int gridW, int gridH, float squareSize)
{
    vector<Point3f> objectPoints;
        for (int i = 0; i < gridH; i++)
            for (int j = 0; j < gridW; j++)
                objectPoints.push_back(Point3f(float(j*squareSize), float(i*squareSize), 0));
    return objectPoints;
}
            vector<Point3f> objectPoints = calcBoardCornerPositions(grids.width, grids.height);

第二个参数

        vector<Point2f> corners;
        bool found = findChessboardCorners(images, grids, corners, CALIB_CB_ADAPTIVE_THRESH + CALIB_CB_NORMALIZE_IMAGE + CALIB_CB_FAST_CHECK);

第三四个参数既是上篇的结果，读入之。

再后两个参数是我们要得到的结果，声明后带入即可。

再其他参数默认就好。

那么得到rvecs, tvecs之后怎么得到棋盘的空间姿态呢，姿态坐标系又是什么呢？

rvecs是旋转向量，使用Rodrigues转成旋转矩阵。原理百度可查。

现在得到了旋转矩阵和平移矩阵了，那么根据标定公式就可以得到世界坐标了。
接下来求解三轴旋转角。原理如下：

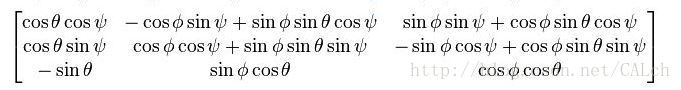
这个矩阵对应与旋转矩阵，由旋转矩阵即可反解欧拉角。

最终效果：

X,Y,Z是以镜头为原点的世界坐标单位0.1mm，ang_X,Y,Z是棋盘沿三轴的旋转角度，单位度。

代码实时运行，速度超过20FPS，精度1cm以内。

完整代码：

#include <cv.h>
#include <highgui.h>
#include <iostream>
#include <math.h>
#define pi 3.14159265358979323846
using namespace std;
using namespace cv;
vector<Point3f> calcBoardCornerPositions(int gridW, int gridH, float squareSize)
{
    vector<Point3f> objectPoints;
        for (int i = 0; i < gridH; i++)
            for (int j = 0; j < gridW; j++)
                objectPoints.push_back(Point3f(float(j*squareSize), float(i*squareSize), 0));
    return objectPoints;
}
vector<Point3f> calcBoardCornerPositions(int gridW, int gridH)
{
    vector<Point3f> objectPoints;
    for (int i = 0; i < gridH; i++)
        for (int j = 0; j < gridW; j++)
            objectPoints.push_back(Point3f(float(j * 89), float(i * 83), 0));
    return objectPoints;
}
int main()
{
    VideoCapture cap(1);
    if (!cap.isOpened()) return -1;
    //cap.set(CV_CAP_PROP_FRAME_WIDTH, 1920);
    //cap.set(CV_CAP_PROP_FRAME_HEIGHT, 1080);
    Mat images, gray;
    Size grids(9, 6);
    int Grids_Size = 260;
    float Ang_X, Ang_Y, Ang_Z;
    float X, Y, Z;
    char key; int i = 0;
    //float A[][3] = { { 644.8137843176841, 0, 302.6526363184274 },{0, 649.3562275395091, 286.5283609342574 },{0, 0, 1 }};
    //float B[] = { 0.01655500980525433, 0.1901812353222618, 0.003461616464410258, 0.002455084197033077, -1.444734184159016 };
    float A[][3] = { { 988.74755, 0, 309.709197 }, { 0, 988.2410178, 239.85705 }, { 0, 0, 1 } };
    float B[] = { -0.41287433, 1.80600373, 0.00250586, 0.0013610796, -7.6232044988 };
    Mat rvecs(3, 1, CV_32F), tvecs(3, 1, CV_32F), cameraMatrix(3, 3, CV_32F), distCoeffs(1, 5, CV_32F), R(3, 3, CV_32FC1);

    for (int i = 0; i < 3; i++)
        for (int j = 0; j < 3; j++)
        {
        cameraMatrix.at<float>(i, j) = A[i][j];
        R.at<float>(i, j) = 0;
        }
    for (int i = 0; i < 5;i++)
    distCoeffs.at<float>(0, i) = B[i];
    namedWindow("chessboard", 0);
    namedWindow("qqq", 0);
    cap >> images;
    while (1)
    {
        cap >> images;
        imshow("qqq", images);
        vector<Point2f> corners;
        bool found = findChessboardCorners(images, grids, corners, CALIB_CB_ADAPTIVE_THRESH + CALIB_CB_NORMALIZE_IMAGE + CALIB_CB_FAST_CHECK);
        if (found) 
        {
            cvtColor(images, gray, CV_BGR2GRAY);
            cornerSubPix(gray, corners, Size(11, 11), Size(-1, -1),
                TermCriteria(CV_TERMCRIT_EPS + CV_TERMCRIT_ITER, 30, 0.1));//0.1为精度
            drawChessboardCorners(images, grids, corners, found);
            vector<Point3f> objectPoints = calcBoardCornerPositions(grids.width, grids.height, Grids_Size);
            //vector<Point3f> objectPoints = calcBoardCornerPositions(grids.width, grids.height);
            solvePnP(objectPoints, corners, cameraMatrix, distCoeffs, rvecs, tvecs);
            Rodrigues(rvecs, R);

            Ang_X = asin(R.at<double>(1, 0) / cos(asin(-R.at<double>(2, 0)))) / pi * 180;
            Ang_Y = asin(-R.at<double>(2, 0)) / pi * 180;
            Ang_Z = asin(R.at<double>(2, 1) / cos(asin(-R.at<double>(2, 0)))) / pi * 180;

            X = R.at<double>(0, 0) *objectPoints[22].x + R.at<double>(0, 1)  * objectPoints[22].y + R.at<double>(0,2)  * objectPoints[22].z + tvecs.at<double>(0,0);
            Y = R.at<double>(1, 0) *objectPoints[22].x + R.at<double>(1, 1)  * objectPoints[22].y + R.at<double>(1, 2)  * objectPoints[22].z + tvecs.at<double>(1, 0);
            Z = R.at<double>(2, 0) *objectPoints[22].x + R.at<double>(2, 1)  * objectPoints[22].y + R.at<double>(2, 2)  * objectPoints[22].z + tvecs.at<double>(2, 0);
            putText(images, "X:"+to_string(X), { 1, 50 }, 0, 1.0f, CV_RGB(255, 0, 0), 2);
            putText(images, "Y:"+to_string(Y), { 1, 150 }, 0, 1.0f, CV_RGB(0, 255, 0), 2);
            putText(images, "Z:"+to_string(Z), { 1, 250 }, 0, 1.0f, CV_RGB(0, 0, 255), 2);
            putText(images, "Ang_X:" + to_string(Ang_X), { 300, 50 }, 0, 1.0f, CV_RGB(255, 0, 0), 2);
            putText(images, "Ang_Y:" + to_string(Ang_Y), { 300, 150 }, 0, 1.0f, CV_RGB(0, 255, 0), 2);
            putText(images, "Ang_Z:" + to_string(Ang_Z), { 300, 250 }, 0, 1.0f, CV_RGB(0, 0, 255), 2);
            imshow("chessboard", images);
        }
        key=waitKey(20);
        if (key == ' ')
            break;
    }
    return 0;
}

注意，代码中取objectPoints[22]计算是求解棋盘较为中间的点的坐标，若取0则是计算的棋盘第一个点坐标，这个不重要。

完了。

接下来如果有空的话把双目的也写上来。还有单目标定也可以用MATLAB工具箱，结果差不多。