% See also http://www.particleincell.com/blog/2012/matlab-fem/
close all
% Load mesh data, coordinates of element 'p' and connectivity 't'==========
load MeshVessel;
% Set nodes of Dirichlet- and Neumann bounaries============================
Neumann=[1 14;14 2;7 25;25 6];
Dirichlet=[4;24;5];
% Inlet velocity===========================================================
V0=5;
% =========================================================================
TotalNumberOfNodes=size(p,1);
NumberOfElements=size(t,1);
% Initialisation of K and F================================================
K=zeros(TotalNumberOfNodes,TotalNumberOfNodes);
F=zeros(TotalNumberOfNodes,1);
% Computation of Ke & assemblage of K======================================
for e=1:NumberOfElements
NodesOfElement=t(e,:);
P=[ones(1,3);p(NodesOfElement,:)'];
AreaOfElement=abs(det(P))/2;
Coeffs=inv(P);
diffPhi=Coeffs(:,2:end);
B{e}=[];
for i=1:3
Bsmall=[diffPhi(i,1);
diffPhi(i,2)];
B{e}=[B{e},Bsmall];
end
Ke=diffPhi*diffPhi'*AreaOfElement;
K(NodesOfElement,NodesOfElement)=K(NodesOfElement,NodesOfElement)+Ke;
end
% F_Gamma==================================================================
for e=1:size(Neumann,1)
knooppunten=Neumann(e,:);
P=p(knooppunten,:);
LengthOfElement=norm(diff(P));
% Value of directional derivative, perpendicular to the edge, and
% pointed inside, resulting in a negative sign
FeGamma=(-V0)*1/2*[1;1]*LengthOfElement;
F(knooppunten)=F(knooppunten)+FeGamma;
end
%==========================================================================
K(Dirichlet,:)=0;% put zeros in boundary rows of K and F
K(Dirichlet,Dirichlet)=eye(numel(Dirichlet),numel(Dirichlet));
% Set Dirichlet boundaries (value of fixed phi)============================
F(Dirichlet)=[0;0;0];
%==========================================================================
phi=K\F;
% Initalize matrix with centroids of each element==========================
Pmean=[];
% Computation of element velocities and magnitude of nodal velocities=====
V=[];
MagnitudesOfNodalVelocities=zeros(TotalNumberOfNodes,1);
for e=1:NumberOfElements
NodesOfElement=t(e,:);
P=[ones(1,3);p(NodesOfElement,:)'];
% Storage of centroids of each element
Pmean=[Pmean;mean(p(NodesOfElement,:))];
Coeffs=inv(P);
diffPhi=Coeffs(:,2:end);
phi_e=phi(NodesOfElement);
% Storage of element velocities [vxe,vye] in V
ve=(diffPhi'*phi_e)'; % velocity in element e
V=[V;ve];
MagnitudeOfVelocity=sqrt(ve(1)^2+ve(2)^2);
MagnitudesOfNodalVelocities(NodesOfElement)=MagnitudesOfNodalVelocities(NodesOfElement)+MagnitudeOfVelocity;
end
% Determine node frequencies (occurrences)=================================
NodeFrequencies=[];
for i=1:TotalNumberOfNodes
NodeFrequencies=[NodeFrequencies;numel(find(t==i))];
end
MagnitudesOfNodalVelocities=MagnitudesOfNodalVelocities./NodeFrequencies;
% Plotting solution========================================================
set(gcf,'color','w');
hold on;
axis equal;
axis off;
for e=1:NumberOfElements
NodesOfElement=t(e,:);
C=p(NodesOfElement,:);
fill(C(:,1),C(:,2),MagnitudesOfNodalVelocities(t(e,:)),'EdgeColor',[0.5,0.5,0.5]);
end
% Plotting velocity vecotrs================================================
quiver(Pmean(:,1),Pmean(:,2),V(:,1),V(:,2),'color',[1 1 0],'LineWidth',1.5)
% Show node numbers========================================================
text(p(:,1),p(:,2),phi,num2str([1:size(p,1)]'),'FontSize',10','Color','k',...
'FontName','Cambria','HorizontalAlignment','left','VerticalAlignment','bottom');
% Computation of streamlines===============================================
Xp=p(:,1);
Yp=p(:,2);
% Timestep
dt=1e-2;
% Locate inital position of particles, add some, loose some================
Particles=[0 ,0.09;
0 ,0.25;
0 ,0.55;
0.0582 ,1.4658;
0.3073 ,1.8348];
% Loop over all elements===================================================
for j=1:size(Particles,1);
counter=0;
particle=Particles(j,:);
for i=1:60
for e=1:NumberOfElements
% Locate the element where the particle is to be found
if inpolygon(particle(1),particle(2),Xp(t(e,:)),Yp(t(e,:)))==1
%==========================================================
POS=[particle(1),particle(2),V(e,1),V(e,2)];
H(4*counter+1:4*(counter+1),j)=[POS];
particle=particle+[V(e,1)*dt,V(e,2)*dt];
counter=counter+1;
break
end
e=NumberOfElements;
end
end
end
% Plot the trajectories====================================================
for k=0:floor(size(H,1)/4)-2
% Plot the final position of the particles=============================
for i=1:size(H,2);
plot([H(4*k+1,i),H(4*(k+1)+1,i)],[H(4*k+2,i),H(4*(k+1)+2,i)],'color',[1 1 1],'LineWidth',1.5);
end
%======================================================================
drawnow
end





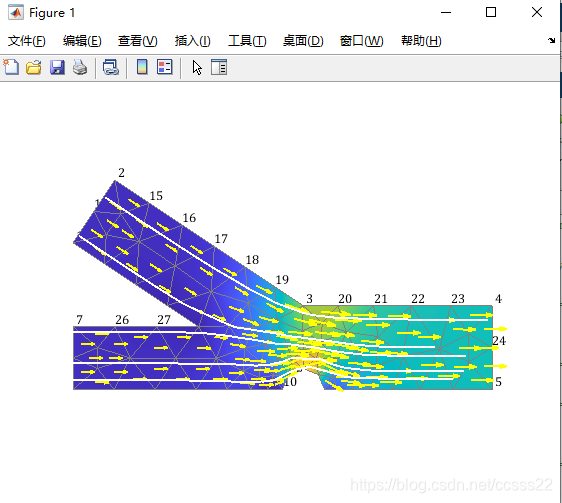
 这段代码展示了如何使用有限元方法求解流体力学问题。它加载网格数据,设定边界条件,计算元素矩阵并组装全局矩阵,接着求解方程组得到速度场,并绘制了速度向量和节点数值。
这段代码展示了如何使用有限元方法求解流体力学问题。它加载网格数据,设定边界条件,计算元素矩阵并组装全局矩阵,接着求解方程组得到速度场,并绘制了速度向量和节点数值。


















 1466
1466


 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?









